ベクトルの一次独立・一次従属は,大学数学における難しい概念の1つでしょう。これは,
\begin{aligned}k_1\boldsymbol{v_1}+k_2\boldsymbol{v_2}+\dots + k_n\boldsymbol{v_n} =\boldsymbol{0} \\ \implies k_1 = k_2=\dots = k_n =0\end{aligned}
であること,と定義されます。これについて,詳しく掘り下げ,具体例も多く確認していきましょう。高校生でも,ある程度は理解できると思います。
ベクトルの一次独立・一次従属の定義
定義は大学向けの一般的なものを記載しますが,分からない場合は, \boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_n} がベクトルであり, k_1,k_2,\ldots, k_n は実数といったスカラーであると思って全く差し支えありません。 つまり,以下で, V はベクトルを要素にもつ集合で, K は実数全体の集合 \mathbb{R} などです。難しい言葉を使いますが,実際そういう意味です。
定義(ベクトルの一次独立・一次従属)
V を K 上のベクトル空間とする。
\boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_n}\in V が一次独立 (線形独立; 線型独立; linearly independent) であるとは, k_1,k_2,\ldots, k_n \in K として,
が成立することである。逆に,これが成立しないとき, \boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_n}\in V は一次従属 (線形従属; 線型従属; linearly dependent) であるという。
k_1 \boldsymbol{v_1}+k_2\boldsymbol{v_2}+\dots + k_n\boldsymbol{v_n} の形のことを, \boldsymbol{v_1},\boldsymbol{v_2},\ldots, \boldsymbol{v_n}\in V の一次結合 (線形結合; 線型結合; linear combination) といいます。
ベクトルが「一次独立」であるとは,その一次結合がゼロだとしたときに,すべての係数がゼロですよと言っているのですね。
ここで,今は \begin{aligned}k_1\boldsymbol{v_1}+\dots + k_n\boldsymbol{v_n} =\boldsymbol{0} \implies k_1 =\dots = k_n =0\end{aligned} と定義しましたが, \impliedby が成立することは明らかですから,定義の \implies の部分は, \iff にしても構いません。
ベクトルの一次独立について,以下が成立します。
定理(ベクトルの一次独立)
次の2つは同値である。
- \begin{aligned} &k_1\boldsymbol{v_1}+\cdots +k_n\boldsymbol{v_n}=\boldsymbol{0}\\ &\implies k_1=\dots =k_n=0 \end{aligned}
- \begin{aligned} &k_1\boldsymbol{v_1}+\cdots +k_n\boldsymbol{v_n}=k'_1\boldsymbol{v_1}+\cdots +k'_n\boldsymbol{v_n}\\ &\implies k_i=k'_i \quad (1\le i\le n) \end{aligned}
1.は一次独立の定義を表しており,2.は「一次結合の表示は一意的である」と言っています。この2つは同等です。
実際,1. \implies 2. については,まず2.を移項して,
(k_1-k'_1)\boldsymbol{v_1}+\dots +(k_n-k'_n)\boldsymbol{v_n}=\boldsymbol{0}
としてから,1.を適用すればよいです。また,2. \implies 1. については,2.の結果を, k'_1 = \dots = k'_n = 0 としてやればよいです。
また,もう少し掘り下げると,ベクトルが一次独立であるとは, \boldsymbol{v_1}, \boldsymbol{v_2}, \ldots \boldsymbol{v_n} のどのベクトルも,他の n-1 個の一次結合で表せないことを意味します。実際もし,
\small\boldsymbol{v_i} = l_1\boldsymbol{v_1} + \cdots + l_{i-1}\boldsymbol{v_{i-1}} + l_{i+1} \boldsymbol{v_{i+1}} + \cdots +l_n\boldsymbol{v_{n}}
のように表せたと仮定すると, (k_1, \ldots, k_n) = (l_1, \ldots, l_{i-1}, -1, l_{i+1}, \ldots, l_n) \ne (0, \ldots ,0) も
の解になってしまい,一次従属となります。
ベクトルの一次独立・一次従属の具体例6つ
ここからは具体的な例を確認し,イメージを膨らませていきましょう。
例1.(平面ベクトル)
\textcolor{red}{\mathbb{R}^2 = \{(x, y) \mid x, y \in \mathbb{R}\} } において,
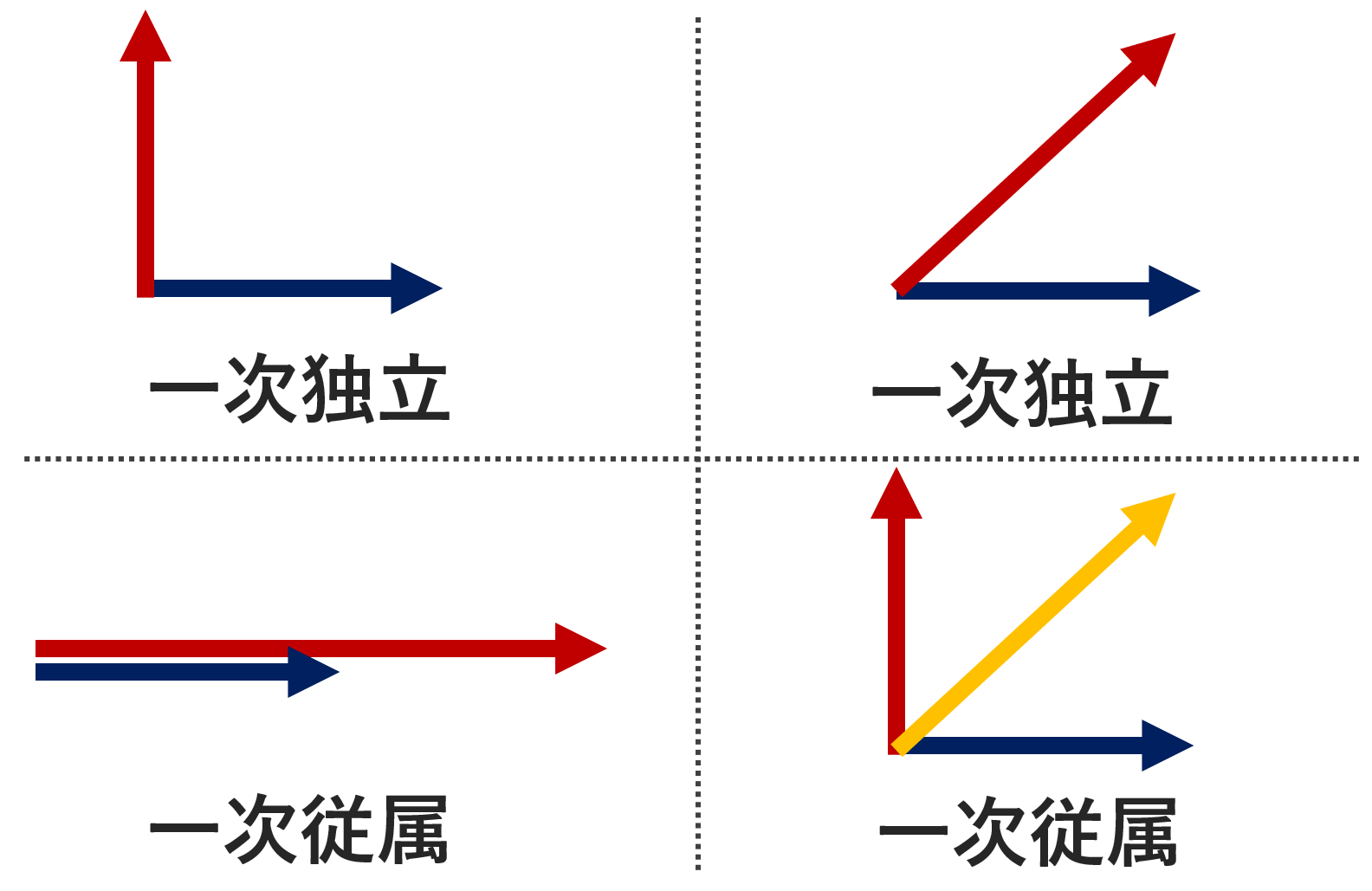
- (1,0), (0, 1) は一次独立である。
- (1, 0), (1,1) は一次独立である。
- (1,0), (2, 0) は一次従属である。
- (1,0), (0,1), (1,1) は一次従属である。
- (0,0), (1,1) は一次従属である。
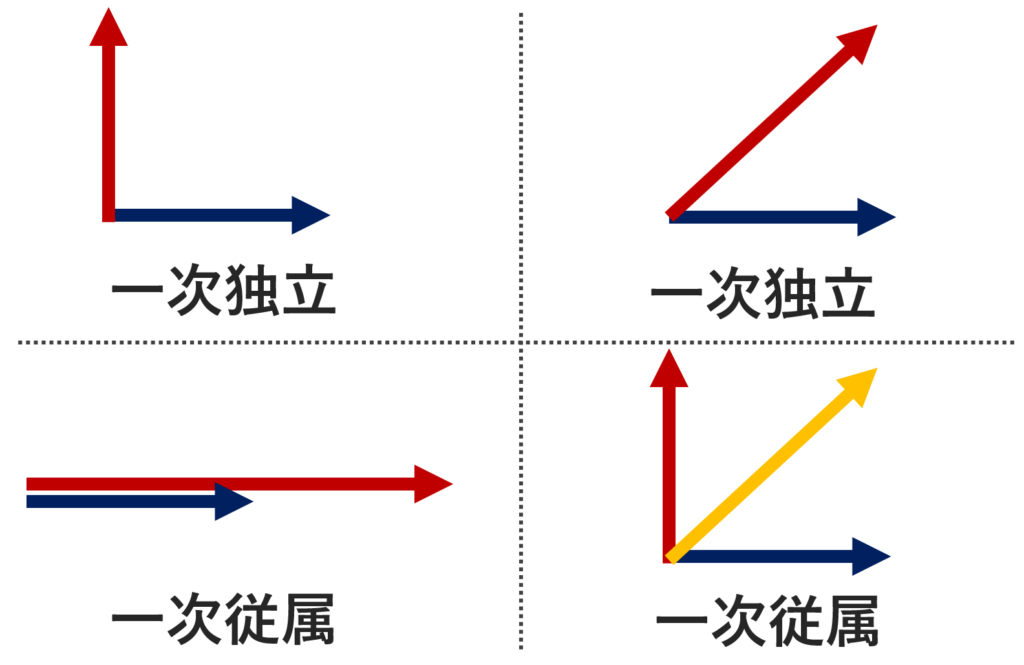
定義に従って,確認してみましょう。
1. k(1,0) + l (0, 1) = (0,0) とすると, (k,l) =(0,0) より, k=l=0.
2. k(1,0) + l (1, 1) = (0,0) とすると, (k+l,l) =(0,0) より, k=l=0.
3. k(1,0) + l (2,0) = (0,0) とすると, (k+2l, 0) =(0,0) であり, k=l=0 でなくてもよい。たとえば, k=2, l=-1 でも良いので,一次従属である。
4. k(1,0) + l (0, 1) +m (1,1)= (0,0) とすると, (k+m, l+m)=(0,0) であり, k=l=m=0 でなくてもよい。たとえば, k=l=1,\; m=-1 でもよいので,一次従属である。
5. l(0,0) +m(1,1) = (0,0) とすると,m=0 であるが, l=0 でなくてもよい。よって,一次従属である。
4.については,どの2つも一次独立ですが,3つ全体としては一次独立にならないことに注意しましょう。また,5.のように, \boldsymbol{0} が入ると,一次独立にはなり得ません。
なお,平面上の2つのベクトルは,平行でなければ一次独立になることが知られています。また,平面上では,3つ以上の一次独立なベクトルは取れないことも知られています。
例2.(空間ベクトル)
\textcolor{red}{\mathbb{R}^3 = \{(x, y, z) \mid x, y, z \in \mathbb{R}\} } において,
- (1,0, 0), (0, 1, 0) は一次独立である。
- (1, 0, 0), (0,1,0), (0,0,1) は一次独立である。
- (1, 0, 0), (2, 1, 3), (3, 0, 2) は一次独立である。
- (1,0,0), (2,0,0) は一次従属である。
- (1,1,1), (1,2,3),(2,4,6) は一次従属である。
\mathbb{R}^3 上では,3つまで一次独立なベクトルが取れることが知られています。
3つの一次独立なベクトルを取るには, (0,0,0) とその3つのベクトルを,座標空間上の4点とみたときに,同一平面上にないことが必要十分であることも知られています。
例3.(n次元ベクトル)
\textcolor{red}{\mathbb{R}^n = \{(x_1,x_2, \ldots, x_n) \mid x_1, x_2, \ldots ,x_n \in \mathbb{R}\} } において, \boldsymbol{e_k} = (0, \ldots, 1, \ldots, 0) , \, 1 \le k \le n (k 番目の要素のみ 1) と定めると,
\boldsymbol{e_1}, \boldsymbol{e_2},\ldots, \boldsymbol{e_n} は一次独立である。
ですから, 右辺を \boldsymbol{0} とすると, k_1=\dots=k_n=0 となりますね。よって一次独立です。(関連記事:数ベクトルの定義と数ベクトルにおけるノルム・内積)
さて,ここからは具体例のレベルを上げましょう。ベクトル空間について,ある程度理解しているものとします。
例4.(数列)
数列全体のなすベクトル空間 \textcolor{red}{l= \{ \{a_n\} \mid a_n\in\mathbb{R} \} } において,
\boldsymbol{e_n} = (0, \ldots, 0, 1, 0 , \ldots) , n\ge 1 (n 番目の要素のみ 1) と定めると,
任意の N\ge 1 に対し, \boldsymbol{e_1}, \boldsymbol{e_2},\ldots, \boldsymbol{e_N} は一次独立である。
これは,例3とやっていることはほぼ同じです。
一次独立は,もともと有限個のベクトルでしか定義していないことに注意しましょう。
例5.(多項式)
多項式全体のなすベクトル空間 \textcolor{red}{\mathbb{R}[x] = \{ a_nx^n + \cdots + a_1x+ a_0 \mid a_0, \ldots ,a_n \in \mathbb{R}, n \ge 1 \} } において,
任意の N\ge 1 に対して, 1,x,x^2,\dots, x^N は一次独立である。
「多項式もベクトルと思える」ことは,ベクトル空間を勉強すれば知っていると思います(→ベクトル空間・部分ベクトル空間の定義と具体例10個)。これについて,
k_1 + k_2 x + \dots+ k_N x^N = 0
とすると, k_1=k_2=\dots = k_N =0 になりますから,一次独立ですね。
例6.(有理数と実数)
実数全体の集合 \color{red}\mathbb{R} を有理数 \mathbb{Q} 上のベクトル空間だと思うと,
1, \sqrt{2} は一次独立である。
有理数上のベクトル空間と思うことがポイントで,実数上のベクトル空間と思えば成立しません。
有理数上のベクトル空間と思うと,一次結合は,
k_1 + k_2\sqrt{2} = 0,\quad \color{red} k_1,k_2\in \mathbb{Q}
と, k_1, k_2 を有理数で考えなければなりません(実数上のベクトル空間だと,実数で考えられます)。すると, k_1=k_2=0 になりますから, 1, \sqrt{2} は一次独立であるというわけです。