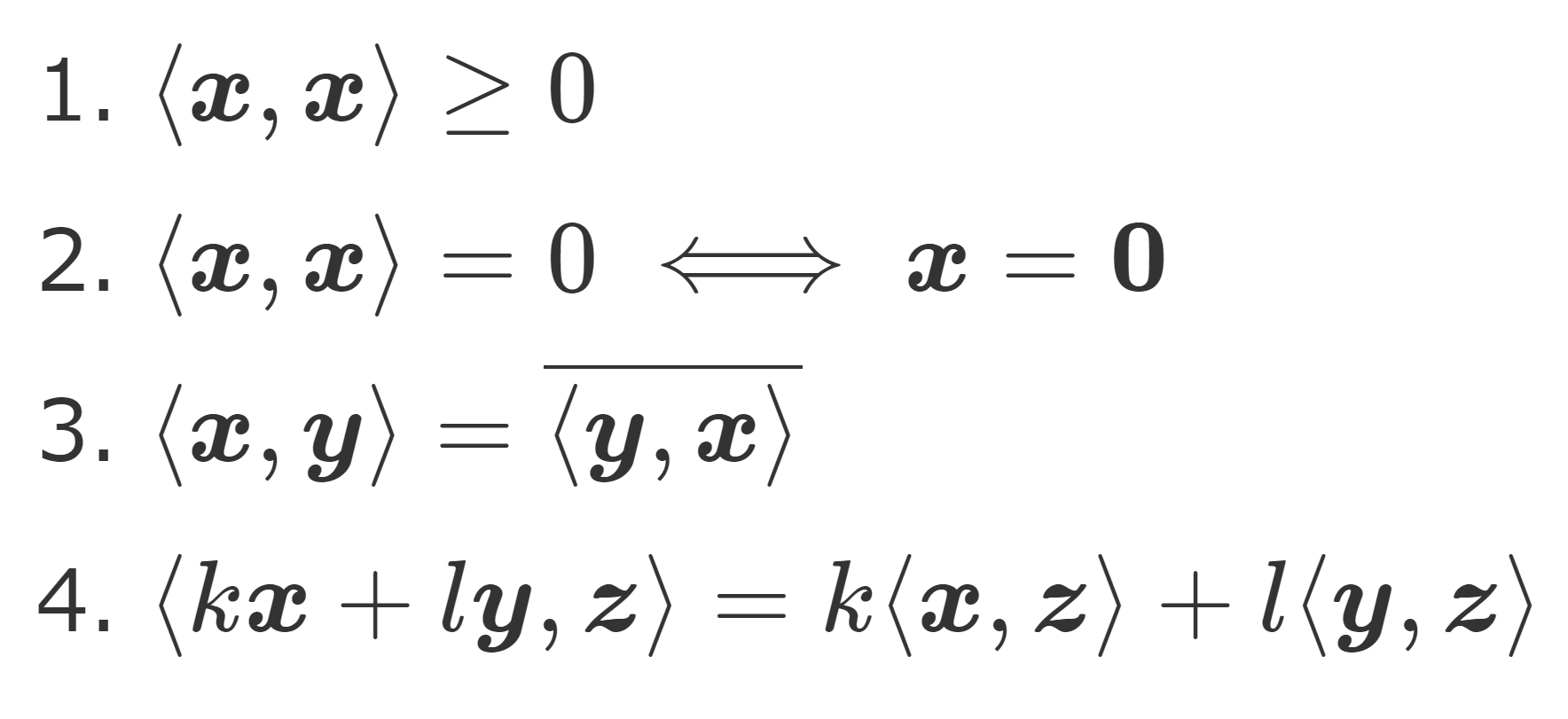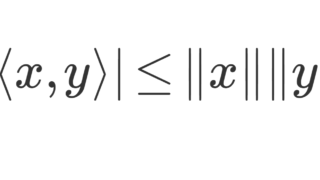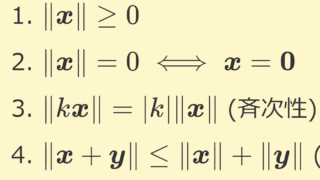【内積空間】内積の定義・具体例と中線定理

内積が定まったベクトル空間のことを，内積空間といいます。内積とは，2つのベクトル同士を「測る」ツールであり，内積が定まるベクトル空間は，「直交」といった概念を導入することが可能です。

内積について，その定義と具体例，さらにノルムとの関係を述べ，ノルムとの関係を扱う上で必要な中線定理についても記述しましょう。

今回は，専門数学における一般的な内積空間を定義します。単に数ベクトル（数字を並べただけのベクトル）に関する内積については，以下の記事の方が平易で分かりやすいと思います。

ベクトル空間における内積とは
内積空間の具体例
内積とノルムの関係と中線定理
1. 内積空間ならばノルム空間である
2. 中線定理をみたすノルム空間は内積空間になる
内積の基本的な性質
完備な内積空間～ヒルベルト空間～
関連する記事

ベクトル空間における内積とは

定義（内積・内積空間・ベクトルの直交）

$V$ を $\mathbb{C}$ 上のベクトル空間(複素ベクトル空間)とする。このとき，関数 $\langle\cdot,\cdot\rangle \colon V\times V\to \mathbb{C}$ が内積 (inner product) であるとは，以下の4つをみたすことをいう。以下， $\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\in V, \,k,l\in\mathbb{C}$ とする。

$\langle \boldsymbol{x},\boldsymbol{x}\rangle\ge 0$
$\langle \boldsymbol{x},\boldsymbol{x}\rangle=0\iff \boldsymbol{x}=\boldsymbol{0}$
$\langle \boldsymbol{x},\boldsymbol{y}\rangle=\overline{ \langle \boldsymbol{y},\boldsymbol{x}\rangle}$ (エルミート対称性)
$\langle k\boldsymbol{x}+l\boldsymbol{y},\boldsymbol{z}\rangle=k\langle \boldsymbol{x},\boldsymbol{z}\rangle+l\langle \boldsymbol{y},\boldsymbol{z}\rangle$ (第一変数に関する線形性)

内積が定義されたベクトル空間を内積空間 (inner product space) あるいは前ヒルベルト空間(pre-Hilbert space) という。

$\boldsymbol{x},\boldsymbol{y}$ に対し， $\langle\boldsymbol{x},\boldsymbol{y}\rangle =0$ が成り立つとき， $\boldsymbol{x}$ と $\boldsymbol{y}$ は直交する (orthogonal) といい，しばしば $\color{red} \boldsymbol{x}\perp\boldsymbol{ y}$ とかく。

なお，内積は $\color{red}\langle\boldsymbol{x},\boldsymbol{y}\rangle$ の他に， $\color{red}(\boldsymbol{x},\boldsymbol{y})$ や $\color{red}\boldsymbol{x}\cdot \boldsymbol{y}$ というかき方もよく用いられる。

3.の上付きバーは複素共役を表します。

今は複素ベクトル空間としましたが， $V$ が $\R$ 上ベクトル空間(実ベクトル空間) のときも内積が考えられます。その内積は， $\langle\cdot,\cdot\rangle \colon V\times V\to \mathbb{R}$ のように，終域を $\R$ とし，上の定義のうち3.を $\langle \boldsymbol{x},\boldsymbol{y}\rangle={ \langle \boldsymbol{y},\boldsymbol{x}\rangle}$ に変えたものになります。

なお，定義の4.で，内積の第一変数に関して線形性を課しましたが，これと3.より，第二変数に関して，

\begin{aligned}\langle \boldsymbol{x},k\boldsymbol{y}+l\boldsymbol{z}\rangle &= \overline{\langle k\boldsymbol{y}+l\boldsymbol{z},\boldsymbol{x}\rangle}\\ &= \overline{k\langle \boldsymbol{y},\boldsymbol{x}\rangle+l\langle \boldsymbol{z},\boldsymbol{x}\rangle}\\ &= \overline{k}\langle \boldsymbol{x},\boldsymbol{y}\rangle+\overline{l}\langle \boldsymbol{x},\boldsymbol{z}\rangle \end{aligned}

ですから， $\color{red}\langle \boldsymbol{x},k\boldsymbol{y}+l\boldsymbol{z}\rangle= \overline{k}\langle \boldsymbol{x},\boldsymbol{y}\rangle+\overline{l}\langle \boldsymbol{x},\boldsymbol{z}\rangle$ が成り立ちます。これを，第二変数に関する反線形性 (antilinear) あるいは共役線形性といいます。

定義より， $\boldsymbol{0}$ は任意のベクトルと直交します。実際，

\begin{aligned}\langle \boldsymbol{0},\boldsymbol{x}\rangle &= \langle \boldsymbol{0}+\boldsymbol{0},\boldsymbol{x}\rangle=\langle \boldsymbol{0},\boldsymbol{x}\rangle +\langle \boldsymbol{0},\boldsymbol{x}\rangle \end{aligned}

ですから， $\langle \boldsymbol{0},\boldsymbol{x}\rangle =0$ ですね。

内積空間の具体例

簡単に具体例を見ておきましょう。まずは数ベクトル空間における具体例です。

例1(数ベクトル空間).

$\mathbb{C}^2$ を $\mathbb{C}$ 上のベクトル空間とみる。 $\boldsymbol{x}=(x_1,x_2)\in\mathbb{C}^2,\; \boldsymbol{y}=(y_1,y_2)\in\mathbb{C}^2$ に対し，

\color{red}\langle\boldsymbol{x},\boldsymbol{y}\rangle = x_1\overline{y_1}+x_2\overline{y_2}

と定めると，これは内積になる。

また， $\R^2$ を $\R$ 上のベクトル空間とみたときは，単に

\color{red}\langle\boldsymbol{x},\boldsymbol{y}\rangle = x_1{y_1}+x_2{y_2}

とすれば，内積になる。

内積になっていることは各自確認してみてください。 $y_1,y_2$ の方は，複素共役を取って計算していることがポイントです。また， $\boldsymbol{x},\boldsymbol{y}\in\R^2$ (実ベクトル空間)のときは，内積は単に第一成分同士の掛け算と，第二成分同士の掛け算の足し算になります。これは，高校数学でやった「内積の成分表示」と同じですね。

なお， $\mathbb{C}^n$ を $\mathbb{C}$ 上のベクトル空間と見たときも同様で， $\boldsymbol{x}=(x_1,\dots, x_n),\; \boldsymbol{y}=(y_1,\dots, y_n)\in\mathbb{C}^n$ に対し，

\color{red} \langle\boldsymbol{x},\boldsymbol{y}\rangle = x_1\overline{y_1}+\dots +x_n\overline{y_n}

と定義されます。

少々難しいですが，関数空間の例も見ておきましょう。

例2(関数空間).

$C[0,1]$ を，連続関数 $f\colon [0,1]\to\mathbb{C}$ 全体の集合とし，これを $\mathbb{C}$ 上のベクトル空間とみる。 $f,g\in C[0,1]$ に対し，

\color{red}\langle f , g\rangle = \int_0^1 f(x)\overline{g(x)}\,dx

と定めると，これは内積になる。

これも，内積になっていることは各自確認してみてください。

内積とノルムの関係と中線定理

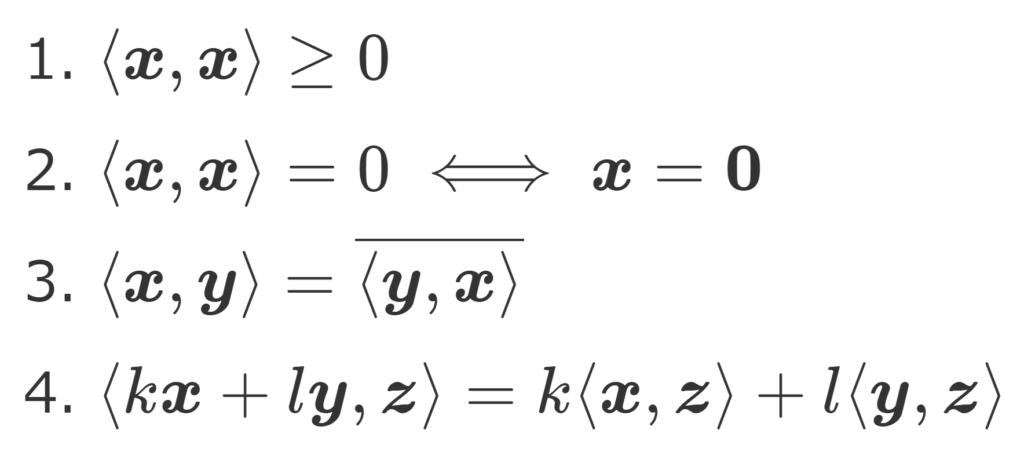
ここからは，内積とノルムの関係について述べましょう。

内積空間ならばノルム空間である

定理1（内積空間 $\implies$ ノルム空間）

$V$ を内積空間とする。このとき，

\begin{equation}\large \color{red} \|\boldsymbol{x}\| = \sqrt{\langle\boldsymbol{x},\boldsymbol{x}\rangle}\end{equation}

によって関数 $\|\cdot\|\colon V\to [0,\infty)$ を定めると，これはノルムになる。

ノルム空間ということは，距離が定まるわけですから，内積空間は収束などの議論ができるわけです。

ノルムの定義を確認しておきましょう。詳しくはノルムとは～ノルム空間の定義と具体例～で解説しています。

ノルムの定義

$\lVert \boldsymbol{x}\rVert \ge 0$
$\lVert \boldsymbol{x}\rVert = 0\iff \boldsymbol{x}=\boldsymbol{0}$
$\lVert k\boldsymbol{x}\rVert =| k|\lVert\boldsymbol{x}\rVert$ (斉次性)
$\lVert \boldsymbol{x}+\boldsymbol{y}\rVert\le \lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert$ (三角不等式)

さて，上のノルムの定義1から4をみたしていることを順番に証明していきましょう。

証明

内積の定義1,2.と定理の枠中 $(1)$ 式より，ノルムの定義1,2.をみたすことは明らか。

ノルムの定義3. $\lVert k\boldsymbol{x}\rVert =| k|\lVert\boldsymbol{x}\rVert$ について

$\lVert k\boldsymbol{x}\rVert = \sqrt{\langle k\boldsymbol{x}, k\boldsymbol{x}\rangle}$ であり，内積の定義3と4より，

\begin{aligned}\langle k\boldsymbol{x}, k\boldsymbol{x}\rangle &= k \langle \boldsymbol{x}, k\boldsymbol{x}\rangle = k\overline{ \langle k\boldsymbol{x}, \boldsymbol{x}\rangle } \\ &= k\overline{k} \overline{\langle \boldsymbol{x}, \boldsymbol{x}\rangle}= |k|^2 {\langle \boldsymbol{x}, \boldsymbol{x}\rangle} \end{aligned}

である。 $\sqrt{ |k|^2 {\langle \boldsymbol{x}, \boldsymbol{x}\rangle}} = |k|\lVert \boldsymbol{x}\rVert$ なので，示された。

ノルムの定義4. $\lVert \boldsymbol{x}+\boldsymbol{y}\rVert\le \lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert$ について

内積の第一変数に関する線形性と，第二変数に関する反線形性(共役線形性)， $\langle \boldsymbol{x},\boldsymbol{y}\rangle=\overline{ \langle \boldsymbol{y},\boldsymbol{x}\rangle}$ より，

\begin{aligned}\|\boldsymbol{x}+\boldsymbol{y}\|^2&= \langle \boldsymbol{x}+\boldsymbol{y},\boldsymbol{x}+\boldsymbol{y}\rangle\\ &= \langle \boldsymbol{x},\boldsymbol{x}+\boldsymbol{y}\rangle+\langle \boldsymbol{y},\boldsymbol{x}+\boldsymbol{y}\rangle\\ &= \langle \boldsymbol{x},\boldsymbol{x}\rangle+\langle \boldsymbol{x},\boldsymbol{y}\rangle+\langle \boldsymbol{y},\boldsymbol{x}\rangle+\langle \boldsymbol{y},\boldsymbol{y}\rangle \\ &= \langle \boldsymbol{x},\boldsymbol{x}\rangle+\langle \boldsymbol{x},\boldsymbol{y}\rangle+\overline{\langle \boldsymbol{x},\boldsymbol{y}\rangle}+\langle \boldsymbol{y},\boldsymbol{y}\rangle \\ &= \lVert\boldsymbol{x}\rVert^2+2\operatorname{Re}\langle \boldsymbol{x},\boldsymbol{y}\rangle+\lVert \boldsymbol{y}\rVert^2 \end{aligned}

なので，

\begin{equation}\|\boldsymbol{x}+\boldsymbol{y}\|^2= \lVert\boldsymbol{x}\rVert^2+2\operatorname{Re}\langle \boldsymbol{x},\boldsymbol{y}\rangle+\lVert \boldsymbol{y}\rVert^2\end{equation}

である。また，

\left(\lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert\right)^2 =\lVert\boldsymbol{x}\rVert^2+2\lVert\boldsymbol{x}\rVert\lVert\boldsymbol{y}\rVert+\lVert \boldsymbol{y}\rVert^2

である。ここで，

\begin{aligned}\operatorname{Re}\langle \boldsymbol{x},\boldsymbol{y}\rangle&\le \left|\operatorname{Re}\langle \boldsymbol{x},\boldsymbol{y}\rangle\right| \le \left|\langle \boldsymbol{x},\boldsymbol{y}\rangle\right|\le \lVert\boldsymbol{x}\rVert\lVert\boldsymbol{y}\rVert\end{aligned}

である。ただし，最後の不等式はコーシーシュワルツの不等式(後の定理3でも記述)である。ゆえに， $\|\boldsymbol{x}+\boldsymbol{y}\|^2\le \left(\lVert \boldsymbol{x}\rVert +\lVert \boldsymbol{y}\rVert\right)^2$ が示された。

証明終

なお，定理1によって定めたノルムは，

\color{red}\|\boldsymbol{x}+\boldsymbol{y}\|^2 + \|\boldsymbol{x}-\boldsymbol{y}\|^2 =2(\|\boldsymbol{x}\|^2 +\|\boldsymbol{y}\|^2)

をみたします。この等式を中線定理 (parallelogram law) といいます。初等幾何でも出てくるやつですね。これを証明しておきましょう。

中線定理の証明

上の証明で出てきた $(2)$ 式と同様に，

\begin{aligned}\|\boldsymbol{x}-\boldsymbol{y}\|^2&= \lVert\boldsymbol{x}\rVert^2-2\operatorname{Re}\langle \boldsymbol{x},\boldsymbol{y}\rangle+\lVert \boldsymbol{y}\rVert^2 \end{aligned}

となるから， $(2)$ 式と上の式の両辺を足し合わせることで，題意が示される。

証明終

$(2)$ 式はよく使う変形なので，覚えておくと良いでしょう。

逆に，中線定理をみたすノルム空間は，内積空間になります。それが次の定理です。

中線定理をみたすノルム空間は内積空間になる

定理2（ノルム空間＋中線定理 $\implies$ 内積空間）

$V$ はノルム空間であり，そのノルムは $\boldsymbol{x},\boldsymbol{y}\in V$ に対し，中線定理

\|\boldsymbol{x}+\boldsymbol{y}\|^2 + \|\boldsymbol{x}-\boldsymbol{y}\|^2 =2(\|\boldsymbol{x}\|^2 +\|\boldsymbol{y}\|^2)

をみたすとする。このとき，

\begin{equation}\color{red}\begin{aligned}\langle \boldsymbol{x}, \boldsymbol{y} \rangle &=\frac{1}{4} ( \lVert \boldsymbol{x}+\boldsymbol{y}\rVert^2 - \lVert \boldsymbol{x}-\boldsymbol{y}\rVert^2 \\ &\quad +i\lVert \boldsymbol{x}+i\boldsymbol{y}\rVert^2 -i\lVert \boldsymbol{x}-i\boldsymbol{y}\rVert^2 )\end{aligned}\end{equation}

と定めると，これは内積になる。 $V$ が実ベクトル空間のときは，

\begin{equation}\color{red}\langle \boldsymbol{x},\boldsymbol{y}\rangle =\frac{1}{4} ( \lVert \boldsymbol{x}+\boldsymbol{y}\rVert^2 - \lVert\boldsymbol{x}-\boldsymbol{y}\rVert^2) \end{equation}

とすればよい。

$(3),(4)$ 式を polarization identity（極化恒等式）といいます。

前節で示したことから，実際はノルム空間＋中線定理 $\iff$ 内積空間です。

この証明は多少手間で，大学の授業だと省略されてしまうことがあります。ここではほぼ自明な部分を除き，ちゃんとやっておきましょう。前半(複素ベクトル空間)の方のみ証明します。

前半の証明

定理2.中の $(3)$ 式で $\boldsymbol{y}=\boldsymbol{x}$ とすることで，

\begin{aligned}&\langle \boldsymbol{x}, \boldsymbol{x} \rangle \\&=\frac{1}{4} ( \lVert \boldsymbol{x}+\boldsymbol{x}\rVert^2 - \lVert \boldsymbol{x}-\boldsymbol{x}\rVert^2 \\ &\quad +i\lVert \boldsymbol{x}+i\boldsymbol{x}\rVert^2 -i\lVert \boldsymbol{x}-i\boldsymbol{x}\rVert^2 ) \\ &= \frac{1}{4} ( \lVert 2\boldsymbol{x}\rVert^2 +i\lVert (1+i)\boldsymbol{x}\rVert^2 -i\lVert(1-i) \boldsymbol{x}\rVert^2 ) \\ &= \lVert \boldsymbol{x}\rVert^2 \end{aligned}

となり，定理1.中の $(1)$ 式と同じ式 $\lVert \boldsymbol{x}\rVert=\sqrt{\langle \boldsymbol{x}, \boldsymbol{x} \rangle }$ を得る。

これにより，ノルムの定義1,2.( $\lVert \boldsymbol{x}\rVert\ge 0,\; \lVert \boldsymbol{x}\rVert=0 \iff \boldsymbol{x}=\boldsymbol{0}$ )から，内積の定義1,2( $\langle \boldsymbol{x},\boldsymbol{x}\rangle\ge 0,\; \langle \boldsymbol{x},\boldsymbol{x}\rangle=0\iff \boldsymbol{x}=\boldsymbol{0}$ )が示される。

内積の定義3( $\langle\boldsymbol{x},\boldsymbol{y}\rangle=\overline{ \langle \boldsymbol{y},\boldsymbol{x}\rangle}$ )については，定理2.中の $(3)$ 式とノルムの性質からほぼ明らかに示せる。

内積の定義4（第一成分に関する線形性）について

まず $\langle \boldsymbol{x}+\boldsymbol{y},\boldsymbol{z}\rangle = \langle \boldsymbol{x},\boldsymbol{z}\rangle+\langle \boldsymbol{y},\boldsymbol{z}\rangle$ を示す。

中線定理 $\|\boldsymbol{a}+\boldsymbol{b}\|^2 + \|\boldsymbol{a}-\boldsymbol{b}\|^2 =2(\|\boldsymbol{a}\|^2 +\|\boldsymbol{b}\|^2)$ において， $\boldsymbol{a}= \frac{1}{2}(\boldsymbol{x}+\boldsymbol{y}+2\boldsymbol{z}),\; \boldsymbol{b}=\frac{1}{2}(\boldsymbol{x}-\boldsymbol{y})$ を代入して整理すると，

\begin{equation}\begin{aligned}&\|\boldsymbol{x}+\boldsymbol{z}\|^2 + \| \boldsymbol{y}+\boldsymbol{z}\|^2 \\&=\frac{1}{2}(\|\boldsymbol{x}+\boldsymbol{y}+2\boldsymbol{z}\|^2 +\|\boldsymbol{x}-\boldsymbol{y}\|^2) \end{aligned}\end{equation}

となる。 $\boldsymbol{z}$ を $-\boldsymbol{z}$ に置き換えることで，

\begin{equation}\begin{aligned}&\|\boldsymbol{x}-\boldsymbol{z}\|^2 + \| \boldsymbol{y}-\boldsymbol{z}\|^2 \\&=\frac{1}{2}(\|\boldsymbol{x}+\boldsymbol{y}-2\boldsymbol{z}\|^2 +\|\boldsymbol{x}-\boldsymbol{y}\|^2) \end{aligned}\end{equation}

もわかる。 $(5)-(6)$ より，

\begin{equation}\begin{aligned}&\|\boldsymbol{x}+\boldsymbol{z}\|^2 + \| \boldsymbol{y}+\boldsymbol{z}\|^2-\|\boldsymbol{x}-\boldsymbol{z}\|^2 - \| \boldsymbol{y}-\boldsymbol{z}\|^2 \\&= \frac{1}{2}(\|\boldsymbol{x}+\boldsymbol{y}+2\boldsymbol{z}\|^2- \|\boldsymbol{x}+\boldsymbol{y}-2\boldsymbol{z}\|^2)\end{aligned}\end{equation}

を得る。 $(7)$ の $\boldsymbol{z}$ を $i\boldsymbol{z}$ に置き換えた式を $(8)$ 式とし， $\frac{1}{4}\{(7)+i(8)\}$ を考えることで，

\begin{equation}\langle \boldsymbol{x},\boldsymbol{z}\rangle+\langle \boldsymbol{y},\boldsymbol{z}\rangle=\frac{1}{2}\langle \boldsymbol{x}+\boldsymbol{y},2\boldsymbol{z}\rangle\tag{9}\end{equation}

を得る。特に， $\boldsymbol{y}=\boldsymbol{0}$ とすると， $\langle \boldsymbol{x},\boldsymbol{z}\rangle=\frac{1}{2}\langle \boldsymbol{x},2\boldsymbol{z}\rangle$ となるが，この $\boldsymbol{x}$ を $\boldsymbol{x+y}$ に置き換えたものを $(9)$ 式の右辺に適用すると，

\langle \boldsymbol{x},\boldsymbol{z}\rangle+\langle \boldsymbol{y},\boldsymbol{z}\rangle=\langle \boldsymbol{x}+\boldsymbol{y},\boldsymbol{z}\rangle

を得る。よって示せた。

最後に， $k\in\mathbb{C}$ に対し， $\langle k\boldsymbol{x},\boldsymbol{y}\rangle=k\langle \boldsymbol{x},\boldsymbol{y}\rangle$ を示す。

$f(k)=\langle k \boldsymbol{x},\boldsymbol{y}\rangle$ とすると，上で示したことより， $k,l\in\mathbb{C}$ に対し， $f(k+l)=f(k)+f(l)$ が成立する。また，内積の連続性(下の定理3参照)より， $f\colon \mathbb{C}\to \mathbb{C}$ は連続である。したがって，コーシーの関数方程式(の複素数版)より，

f(k)= k\langle \boldsymbol{x},\boldsymbol{y}\rangle

である。よって示せた。

証明終

かなり長くなってしまいましたが，何とか示せました。

内積の基本的な性質

既にこれまでの証明でも使った定理ですが，以下は内積の最も基本的な性質といえるでしょう。

定理3（内積の基本的な性質）

$V$ を内積空間とする。このとき，

任意の $\boldsymbol{x},\boldsymbol{y}\in V$ に対し，
$\color{red}\large |\langle \boldsymbol{x},\boldsymbol{y}\rangle|\le \|\boldsymbol{x}\|\|\boldsymbol{y}\|$
が成り立つ。これをコーシーシュワルツの不等式 (Cauchy－Schwarz’s inequality) という。
$\boldsymbol{x_n}\to \boldsymbol{x},\; \boldsymbol{y_n}\to \boldsymbol{y}$ のとき，
$\color{red}\large\langle \boldsymbol{x_n},\boldsymbol{y_n}\rangle \to \langle \boldsymbol{x},\boldsymbol{y}\rangle$
が成り立つ(内積の連続性)。

コーシーシュワルツの不等式については，別の記事に預けることにし，今回はコーシーシュワルツの不等式を認めたうえで2.の証明を行いましょう。

証明

1.について

これはコーシーシュワルツの不等式のさまざまな形と証明で証明している。今回既にさまざまな証明で本不等式を用いているが，証明が循環していないことを確認したい。

2.について

絶対値の三角不等式と1.のコーシーシュワルツの不等式より，