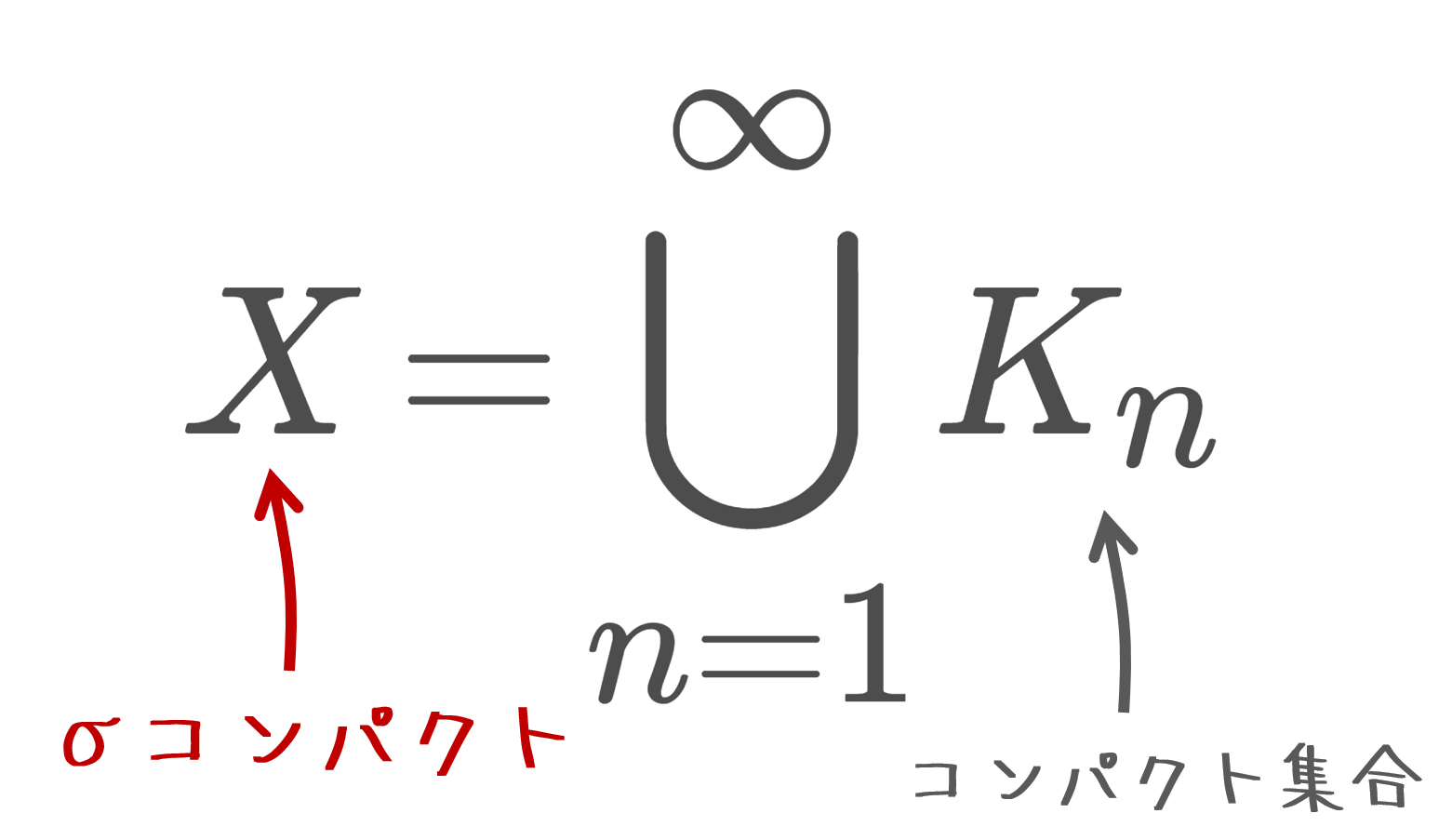K位相(スミルノフ位相)とは,通常の \R の位相に,F_m=\{ 1/n \mid n\ge m\} を閉集合に加えた位相空間です。連結だが局所連結でない,メタコンパクトだがパラコンパクトでない等の性質をもちます。
K位相(スミルノフ位相)について,その定義と性質をていねいにまとめましょう。
K位相(スミルノフ位相)の定義
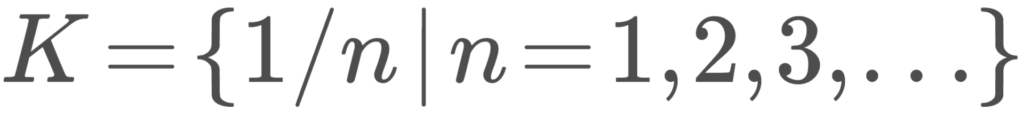
定義(K位相・スミルノフ位相)
K= \{ 1/n\mid n=1,2,3,\ldots\} とする。実数の集合 \R において,
\color{red} \mathcal{B}_K = \{ (a,b)\mid a<b\}\cup \{(a,b)\setminus K\mid a<b\}
を開基とする位相 \mathcal{O}_K をK位相 (K-topology) またはスミルノフ位相 (Smirnov’s deleted sequence topology) という。
\R における通常の位相を \mathcal{O} とすると,
\mathcal{O}_K = \{ O\setminus L\mid O\in\mathcal{O},\, L\subset K\}
と表せる。
特に, \mathcal{O}_K は通常の位相 \mathcal{O} より大きい(細かい・強い)です。すなわち,\mathcal{O}\subset \mathcal{O}_K が成立します。
定義より, K は閉集合になります。F_m=\{ 1/n \mid n\ge m\} も閉集合です。
K位相(スミルノフ位相)の性質とその証明
可算公理・分離公理・コンパクト性・連結性を順番に紹介しましょう。
K位相(スミルノフ位相)と可算公理
第二可算であることは,
\{ (p,q)\mid p,q\in\mathbb{Q}\}\cup \{ (p,q)\setminus K\mid p,q\in\mathbb{Q}\}
が可算開基であることから分かります。また,第二可算ならば第一可算です。また可分であることは, \overline{\mathbb{Q}}=\R が, (\R, \mathcal{O}_K) でも成り立つことから分かります。
K位相(スミルノフ位相)と分離公理
| T_0, T_1, T_2 (ハウスドルフ空間) | T_3 | T_4,T_5 |
|---|---|---|
| 〇 | × | × |
本記事では, T_0 から T_5 は以下のように定義しています。この定義は文献によって変わりますから,注意してください。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 (Kolmogorov space) | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 (Hausdorff space) | 任意の異なる2点 x,y\in X に対して, x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して, F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な空でない閉集合 F,G\subset X に対して, F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合 A,B\subset X に対して, A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
T_3, T_4, T_5 が成り立たないことから,K位相は距離化不可能です。
(\R,\mathcal{O}_K) が T_0, T_1, T_2 であることは,通常の位相 (\R,\mathcal{O}) がそうであることと, \mathcal{O}\subset\mathcal{O}_K から直ちに分かります。
T_3, T_4, T_5 でないことを示しましょう。 K=\{1/n\mid n=1,2,3,\ldots\} 自身は (\R,\mathcal{O}_K) における閉集合ですが, K を含む開集合は,必ず 0\notin K を含みます。よって,1点 0 と閉集合 K は開集合で分離できません。よって T_3 ではありません。
同様に,閉集合 \{0\} と閉集合 K も開集合で分離できないので, T_4 でもありません。 T_4 でなければ定義から明らかに T_5 でもありません。
K位相(スミルノフ位相)とコンパクト性
コンパクト性にまつわる定義は,以下の通りです。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| 可算パラコンパクト (countably paracompact) | 任意の可算開被覆が局所有限な(すなわち,各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち,各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
コンパクトや点列コンパクトでないことは,通常の位相空間 (\R, \mathcal{O}) がコンパクト・点列コンパクトでないことから分かります。また,K位相では, [0,1] もコンパクトではありません。実際,開被覆
\small (\R \setminus K) \cup \bigcup_{n=1}^\infty \left( \frac{1}{n}-\frac{1}{2n(n+1)}, \frac{1}{n}+\frac{1}{2n(n+1)} \right)
は有限部分被覆を持ちません。また, [0,1]\setminus K も開被覆 \bigcup_{n=1}^\infty (1/(n+1),1/n ) が有限部分被覆をもたないため,コンパクトではないです。同じ理由で, 0 の近傍は常にコンパクトではないので, (\R, \mathcal{O}_K) は局所コンパクトでもありません。一方で,
より,σコンパクトは言えます。σコンパクトならばリンデレーフなので,リンデレーフであることも言えます。
可算パラコンパクトでないことと,メタコンパクトであることを証明しましょう。
可算パラコンパクトでないこと・メタコンパクトであることの証明
可算パラコンパクトでないこと
U_n= (\R\setminus K)\cup \{1/n\} とすると, \{U_n\} は (\R, \mathcal{O}_K) の可算開被覆になるが,この局所有限な開細分は存在しない。なぜなら, 0 の任意の近傍 V は,ある N\ge 1 が存在して,
0\in \left(-\frac{1}{N}, \frac{1}{N}\right)\setminus K \subset V
をみたすが,一方で, U_n の開細分 V_n が \R を被覆するためには, 1/n\in V_n でなければならず, V_n は開集合なので, V_n は 1/n のある近傍を含む。よって, n>N のとき, V\cap V_n\ne \emptyset となるため, V は無限個の V_n と交わる。したがって,可算パラコンパクトではない。
メタコンパクトであること
\{U_\lambda\}_{\lambda\in\Lambda} \subset \mathcal{O}_K を開被覆とする。\mathcal{O}_K の定義より,各 \lambda\in\Lambda に対し,ある O_\lambda\in\mathcal{O} と L_\lambda\subset K が存在して,
U_\lambda =O_\lambda\setminus L_\lambda
とかける。このとき, \{O_\lambda\} は通常の位相 (\R,\mathcal{O}) における開被覆になっているから,点有限な \mathcal{O}-開細分 \{P_\phi\} が存在する。このとき, \{P_\phi\setminus K\} は \{U_\lambda\} の点有限な \mathcal{O}_K-開細分になっているが,これは \R\setminus K しか被覆しない。
そこで, 1/n\in U_\lambda となる \lambda\in\Lambda に対し,
\small\begin{aligned}\frac{1}{n} &\in I_n \\&\subset U_\lambda\cap \left( \frac{1}{n}-\frac{1}{2n(n+1)}, \frac{1}{n}+\frac{1}{2n(n+1)} \right)\end{aligned}
となる開区間 I_n をとって, \{P_\phi\setminus K\}\cup \{I_n\} を考えると,これは点有限な \mathcal{O}_K-開細分で,\R を被覆している。よって,メタコンパクトであることが示せた。
証明終
K位相(スミルノフ位相)と連結性
K位相は,連結だが局所連結・弧状連結ではない例の一つになっています。
証明
連結であること
部分空間 \R\setminus \{0\} における開集合の概念は,K位相 \mathcal{O}_K と通常の位相 \mathcal{O} で一致している。すなわち (\R\setminus \{0\},\mathcal{O}_K) と (\R\setminus \{0\},\mathcal{O}) は同相(位相同型)である。
(\R,\mathcal{O}_K) が連結でないと仮定する。すなわち,\mathcal{O}_K-開集合 U,V\subset \R で, U\cap V=\emptyset かつ U\cup V=\R とできるとする。上の議論より,
- U=(-\infty, 0), \quad V=[0, \infty)
- U=(-\infty, 0], \quad V=(0, \infty)
- U= \R\setminus\{0\},\quad V=\{0\}
のいずれかであるが,1.のときは V が開集合でないし,2.のときは U が開集合でないし,3.のときは V が開集合でない。よって,連結である。
局所連結でないこと
\varepsilon>0 とする。0 の開近傍 (-\varepsilon,\varepsilon )\setminus K に含まれる連結集合は存在しないので,局所連結ではない。
弧状連結でないこと
(\R,\mathcal{O}_K) が弧状連結であると仮定する。通常の位相を \mathcal{O} とする。このとき, f(0)=0, \, f(1)=1 となる連続写像 f\colon ([0,1],\mathcal{O})\to (\R, \mathcal{O}_K) が存在する。
f([0,1]) はコンパクトかつ連結な集合の連続像なので,コンパクトかつ連結である。 \mathcal{O}\subset \mathcal{O}_K より, f([0,1]) は \mathcal{O} の意味でも連結である。 0,1\in f([0,1]) なので, [0,1]\subset f([0,1]) である。
f([0,1]) は \mathcal{O}_K の意味でコンパクトなので,その閉部分集合である [0,1] も \mathcal{O}_K の意味でコンパクトなはずであるが,実際はそうではないから,矛盾している。したがって,弧状連結でない。
証明終