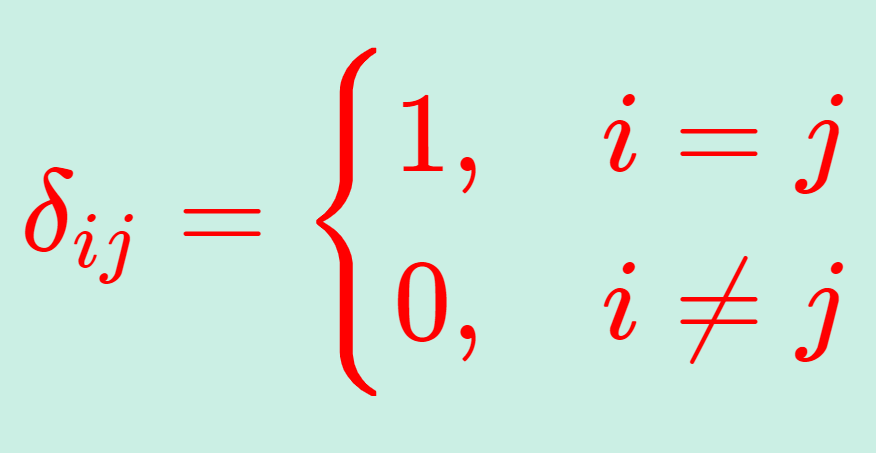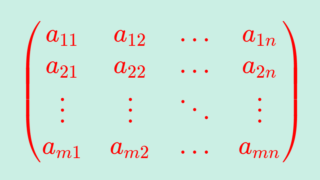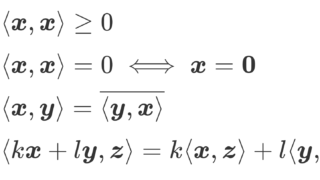クロネッカーのデルタはそれ自身難しいものではなく,いわゆる「便利記号」の一つです。そんなクロネッカーのデルタについて解説します。
クロネッカーのデルタの定義
定義(クロネッカーのデルタ)
\textcolor{red}{\delta_{ij} = \begin{cases} 1, & i=j \\ 0, & i \ne j \end{cases}}
と定義される \delta_{ij} をクロネッカーのデルタ (Kronecker delta) という。
添え字の値が同じならば 1 ,違えば 0 となるわけですね。
クロネッカーのデルタの使用例
例1.(単位行列)
単位行列
\left( \begin{array}{cccc}
1 & 0 & \ldots & 0 \\
0 & 1 & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & 1
\end{array} \right)
はクロネッカーのデルタを用いて
(\delta_{ij} )とかける。
例2.(正規直交基底)
\boldsymbol{e_n} を内積空間(内積が備わったベクトル空間)における正規直交基底とすると,その内積について,
\langle \boldsymbol{e_i}, \boldsymbol{e_j}\rangle = \delta_{ij}
とかける。
頻繁に出てくるわけではないかもしれませんが,注釈なしで,記号だけで出てくることがあり得るので,覚えておくようにしましょう。