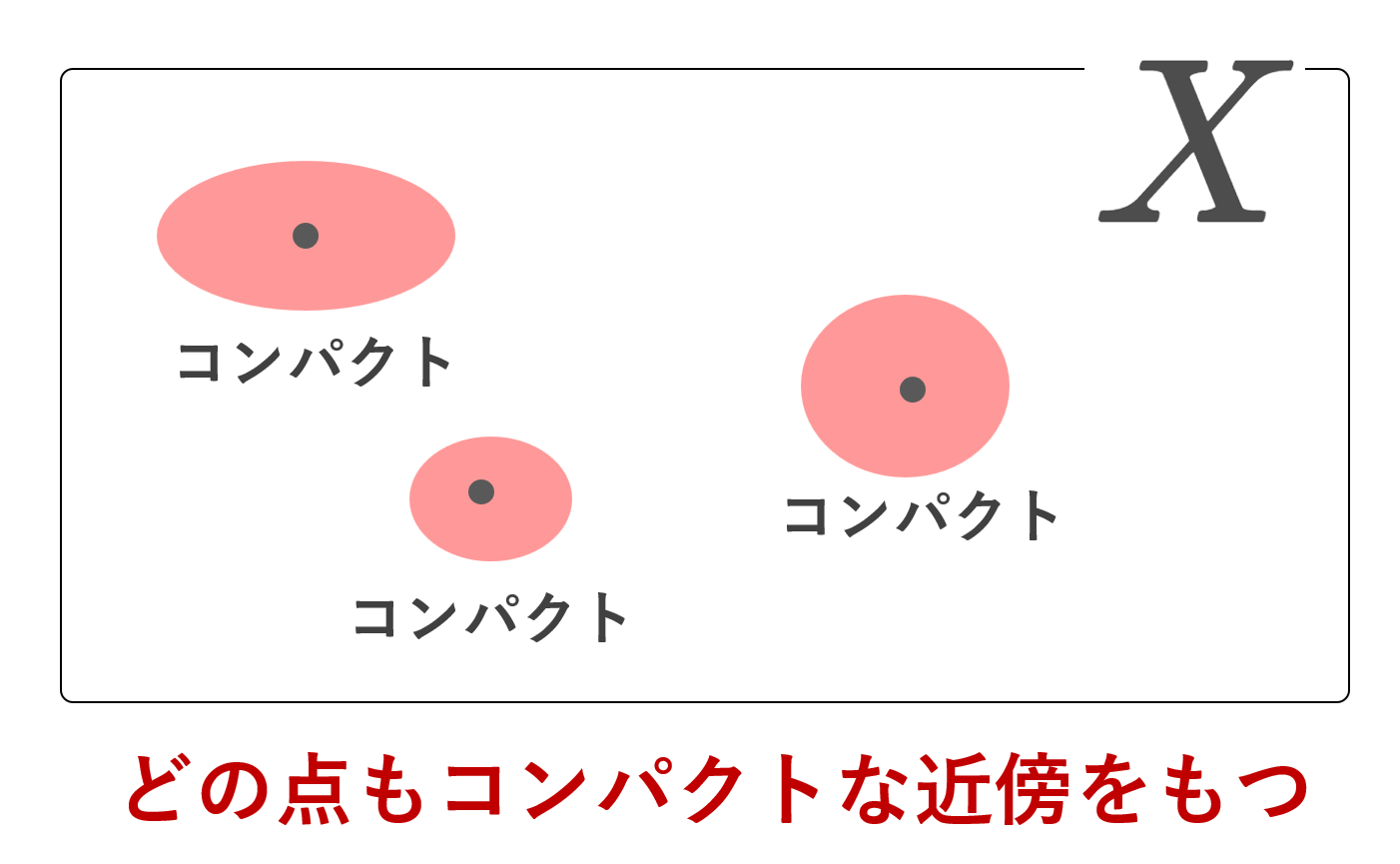
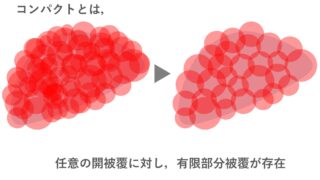
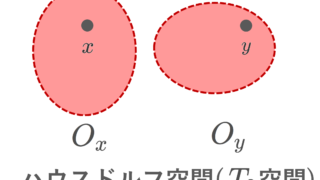
位相空間における局所コンパクト空間とは,各点がコンパクトな近傍を持つ空間のことを言います。ただし,文献によって定義が異なることがあるため,注意が必要です。
本記事では,局所コンパクトの,さまざまな流儀の定義を紹介し,その定義がハウスドルフ空間のときは同値になることや,その他局所コンパクト空間・局所コンパクトハウスドルフ空間の性質を証明付きで解説します。
局所コンパクトの定義
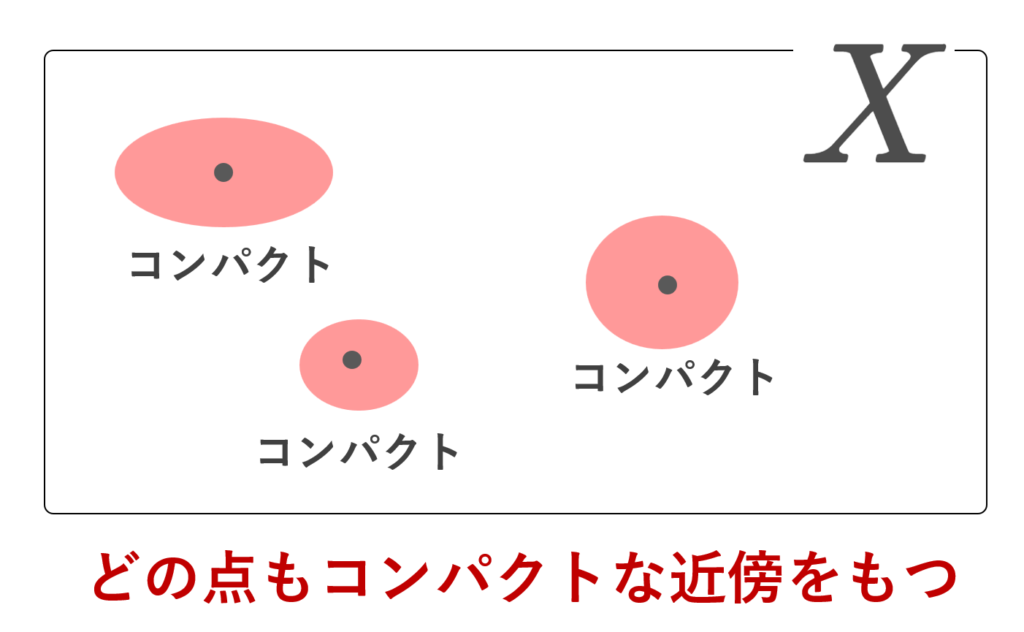
位相空間におけるコンパクトとは,ものすごく扱いやすい性質で,成り立っていると非常に嬉しい性質です。しかし,現実にはコンパクトは性質が良すぎて成り立たないことが多いので,もう少し弱くしたものを考えます。それが局所コンパクトです。
定義(局所コンパクト・強局所コンパクト)
(X,\mathcal{O}) を位相空間とする。このとき,次の4つの条件を考える。
- 任意の x\in X に対し, x のコンパクトな近傍が存在する
- 任意の x\in X に対し, x のコンパクトな閉近傍が存在する
- 任意の x\in X に対し, x のコンパクトな基本近傍系が存在する
- 任意の x\in X に対し, x のコンパクトで閉な基本近傍系が存在する
本記事では,1.を局所コンパクト (locally compact) といい,2.を強局所コンパクト (strongly locally compact) または局所相対コンパクト (locally relatively compact) という。
1.から4.まで紹介したのは,文献によって定義が異なることがあるからです。例えば,内田伏一「集合と位相」や松坂和夫「集合・位相入門」やKelly, General Topologyは,本サイトと同じく局所コンパクトを1.で定義しています。Counterexamples in Topologyも局所コンパクトを1.で定義しており,強局所コンパクトを2.で定義しています。一方で,Willard, General Topologyは,局所コンパクトを3.で定義しています。
Engelking, General Topologyは局所コンパクトを2.で定義していますが,そもそもコンパクトの定義にハウスドルフ性を含んでいます。本記事ではそういうことはしていないことに注意してください。
X がコンパクトなら明らかに(1.の意味で)局所コンパクト・(2.の意味で)強局所コンパクトです。しかし,一般に1.から4.は同値ではありません。4.\implies 3.\implies 1.や 4.\implies 2.\implies 1.は成り立ちますが,逆は成り立ちません。例を確認しておきましょう。
| 名称 | コンパクト | 1. 局所コンパクト | 2. 強局所コンパクト | 3. | 4. |
|---|---|---|---|---|---|
| 密着空間 | 〇 | 〇 | 〇 | 〇 | 〇 |
| \R・無限集合における離散空間 | × | 〇 | 〇 | 〇 | 〇 |
| \mathbb{Q} | × | × | × | × | × |
| \mathbb{Q} の1点コンパクト化(※A) | 〇 | 〇 | 〇 | × | × |
| 無限集合における補有限位相 | 〇 | 〇 | 〇 | 〇 | × |
| 無限集合における特定点位相(※B) | × | 〇 | × | 〇 | × |
| 無限集合における除外点位相 | 〇 | 〇 | 〇 | 〇 | × |
| ※Aと※Bの直和 | × | 〇 | × | × | × |
ただし,もしX がハウスドルフ( T_2)ならば,1.から4.は全て同値であることが知られています。後の定理3で証明しましょう。
局所コンパクト空間の性質
定義の1.を採用して,局所コンパクト空間の性質を見ていきましょう。
以下で,A\subset X が局所コンパクトというときには, A は X の部分空間とみて局所コンパクト空間という意味です。
1. 局所コンパクト空間と写像
開写像でなく,連続だけでは f(X) が局所コンパクトとは限りません。これはコンパクトの連続像は常にコンパクトであることは対照的です。
たとえば, (X,\mathcal{O}) を局所コンパクトでない空間(たとえば \mathbb{Q})とし, (X, 2^X) を,位相のみ離散位相に取り換えたものとします。このときの恒等写像 \operatorname{id}\colon (X, 2^X)\to (X,\mathcal{O}) は連続ですが,開写像ではなく,また像は局所コンパクトではありません。
定理1の証明
y\in f(X) とする。 x\in f^{-1}(\{y\}) とすると,X は局所コンパクトなので,コンパクトな近傍 x\in K\subset X が取れる。 f は連続なので, f(K)\subset f(X) はコンパクトであり, f は開写像なので,y\in f(K) は y の近傍である。
よって, y のコンパクトな近傍 f(K)\subset f(X) が取れたので, f(X) は局所コンパクトである。
証明終
本定理は,局所コンパクトを,定義の3.の意味で捉えても成り立ちます。
なお, X が局所コンパクトでも,そのある商空間 X/\sim が局所コンパクトであるとは言えません。射影は連続ですが,開写像とは限りません。具体例は商位相と商写像の記事内で取り上げています。
2. 局所コンパクト空間と直積
定理2(局所コンパクト空間と直積)
\{(X_\alpha, \mathcal{O}_\alpha)\}_{\alpha\in \Alpha} を空でない位相空間の族とし, X=\prod_{\alpha\in \Alpha} X_\alpha をその直積空間とする。このとき,以下は同値である。
- X は局所コンパクト
- 全ての X_\alpha は局所コンパクトであり,かつ有限個の \alpha を除く全ての X_\alpha はコンパクトである
単に局所コンパクトの直積が局所コンパクトになるわけではなく,直積が局所コンパクトになるには,有限個を除く全てでコンパクトでなければなりません。
以下の証明で, \alpha\in\Alpha に対し, p_\alpha\colon X\to X_\alpha を自然な射影とします。
定理2の証明
1.\implies 2.について
x=(x_\alpha) \in X とする。 X は局所コンパクトなので, x のコンパクトな近傍 K\subset X が取れる。
K は x の近傍なので, x\in U\subset K となる開基 U が取れる。直積位相の(一般的な)開基はある n \ge 1 と異なる \alpha_1, \ldots, \alpha_n\in \Alpha と U_{\alpha_1}\in \mathcal{O}_{\alpha_1},\ldots, U_{\alpha_n}\in \mathcal{O}_{\alpha_n} を用いて
U=U_{\alpha_1}\times\cdots\times U_{\alpha_n}\times\prod_{\alpha\in \Alpha\setminus\{\alpha_1,\ldots, \alpha_n\} } X_\alpha
とかける。射影 p_\alpha は連続なので, p_\alpha(K) はコンパクトである。 k=1,2,\ldots, n に対し,
なので, x_{\alpha_k}\in X_{\alpha_k} がコンパクトな近傍 p_{\alpha_k}(K) をもつため, X_{\alpha_k} は局所コンパクトである。また, \alpha\in \Alpha\setminus\{\alpha_1,\ldots,\alpha_n\} に対し, p_\alpha(K)=X_\alpha なので, X_\alpha はコンパクトである。よって,2.が示せた。
2.\implies 1.について
n\ge 1,\, \alpha_1,\ldots,\alpha_n\in \Alpha とし, \alpha\in \Alpha\setminus\{\alpha_1,\ldots,\alpha_n\} に対し, X_\alpha はコンパクトと仮定する。
x=(x_\alpha)\in X とする。 k=1,\ldots, n に対し, X_{\alpha_k} は局所コンパクトなので,
x_{\alpha_k}\in K_{\alpha_k}\subset X_{\alpha_k}
となる x_{\alpha_k} のコンパクトな近傍 K_{\alpha_k} が存在する。チコノフの定理より,コンパクトの直積はコンパクトなので,
はコンパクトである。さらにこれは x の近傍でもある。したがって, X は局所コンパクトである。
証明終
局所コンパクトハウスドルフ空間
局所コンパクト空間の中でも,特に性質が良いのが,局所コンパクトハウスドルフ空間です。局所コンパクトは位相が小さい(弱い・粗い)ほど成り立ちやすい性質ですが,ハウスドルフは,逆に位相が大きい(強い・細かい)方が成り立ちやすい性質です。よって,局所コンパクトハウスドルフ空間とは,絶妙に良い位相をもった空間と言えます。また,実際に数学で扱う多くの位相空間が局所コンパクトハウスドルフ空間です。ここからは局所コンパクトハウスドルフ空間についての性質を見ていきましょう。
なお,より強くコンパクトハウスドルフ空間の性質についての解説は,ハウスドルフ空間(T2空間)の定義・具体例・性質を詳しくの中で行っています。
ナンバリングは先ほどの続きから始めます。
3. ハウスドルフのときの局所コンパクトの同値な性質
定義で紹介した4つの性質は,ハウスドルフ空間においては同値になります。
定理3(ハウスドルフのときの局所コンパクトの同値な性質)
(X,\mathcal{O}) をハウスドルフ空間( T_2 空間)とする。このとき,次の4つは同値である。
4.\implies 3.\implies 1.や 4.\implies 2.\implies 1.は明らかなので,それ以外を示しましょう。
証明
ハウスドルフ空間のコンパクト集合は閉集合なので,1. \iff 2.,3.\iff 4.である。
あとは 2.\implies 3.を示せばよい。 x\in X とし, x の任意の開近傍 U を取ろう。示すべきことは,x\in W\subset U となる x のコンパクトな近傍 W が取れることである。
2.の仮定より, x の相対コンパクト(すなわち閉包がコンパクト)な開近傍 K を取ることができる。 \overline{K}\subset U なら証明が終わってしまうので, \overline{K}\setminus U\ne\emptyset とする。
\overline{K}\setminus U はコンパクト集合 \overline{K} の閉部分集合なのでコンパクトであり,また \{x\} もコンパクト集合である。ハウスドルフ空間における交わらない2つのコンパクト集合は開集合によって分離できるから,
\overline{K}\setminus U\subset V_1,\, \{x\}\subset V_2, \, V_1\cap V_2=\emptyset
となる開集合 V_1, V_2\subset X が取れる。
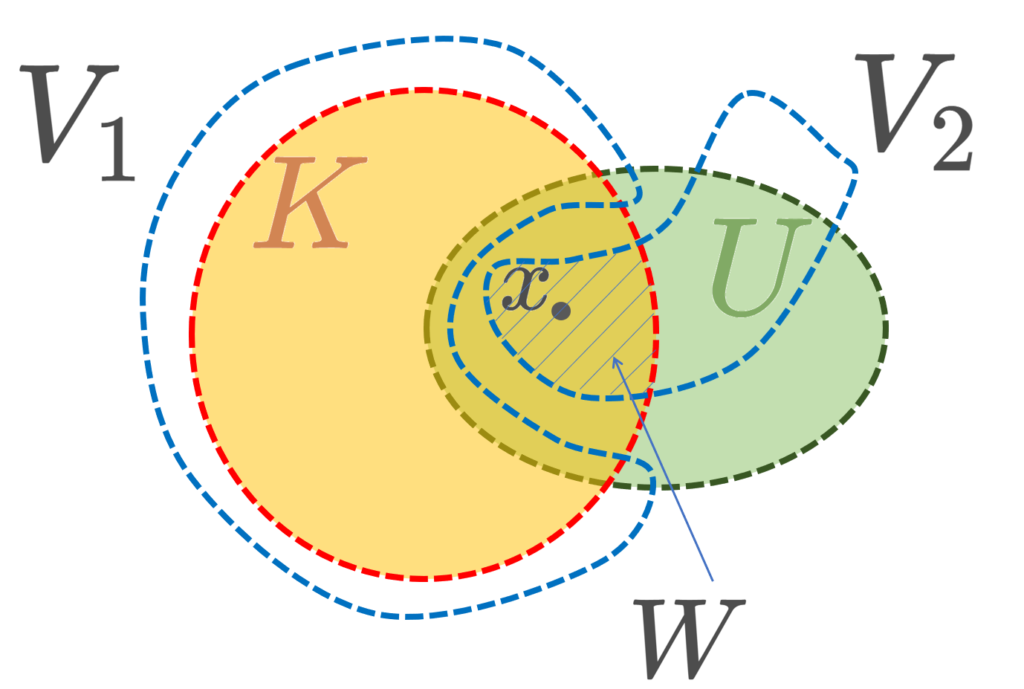
W=K\cap V_2 と定めると,x\in W かつ W は開集合なので, W は x の開近傍であり, \overline{W}=\overline{K\cap V_2}\subset \overline{K}\cap \overline{V_2} (→【位相空間】閉包とは~定義と例と性質~)はコンパクト集合 \overline{K} の閉部分集合なのでコンパクトである。よって示せた。
証明終
4. 局所コンパクトハウスドルフ空間は正則(T3)
定理4(局所コンパクトハウスドルフ空間と分離公理)
局所コンパクトハウスドルフ空間は正則( T_3)である。
この証明は,ハウスドルフ空間(T2空間)の定義・具体例・性質を詳しくの中にあります。
5. ハウスドルフ空間の部分空間が局所コンパクトになる条件
定理5(ハウスドルフ空間の部分空間が局所コンパクトになる条件)
(X,\mathcal{O}) を局所コンパクトハウスドルフ空間( T_2 空間)とし, A\subset X とする。このとき,次の2つは同値である。
- A は局所コンパクト
- ある開集合 U と閉集合 F が存在して, A=U\cap F とかける
より一般に,1.\implies 2.は (X,\mathcal{O}) が単にハウスドルフ空間( T_2 空間)で成立する。
2.\implies 1.は, (X,\mathcal{O}) が単にハウスドルフ空間( T_2 空間)では成立しません。 A=Xが反例です。
証明
2.\implies 1.について
x\in A\subset U とする。 X が局所コンパクトであることと,定理3より, x の X におけるコンパクト閉近傍 x\in K\subset U が存在する。ここで, x\in K\cap F であり, K\cap F は K の閉部分集合なので, X の位相でコンパクトである。 K\cap F\subset A より, A の位相でもコンパクトである。
K\cap F = K\cap F\cap U = K\cap A より, K\cap F は部分空間 A における x の近傍になっているから, x\in A はコンパクトな近傍を持つことが分かったので, A は局所コンパクトである。
1.\implies 2.については,「より一般に~」以下を示す
結論の U\cap F は部分空間 F における開集合である。F=\overline{A} とすればよいので, A が部分空間 \overline{A} における開集合であることを示せばよい。 x\in A を任意に取る。
A は局所コンパクトハウスドルフ空間より,定理3から,ある x\in V\subset A が存在して, V は部分空間 A における開集合かつ \overline{V}^A がコンパクトであるものが取ってこれる。ただし,\overline{\hspace{2pt}\cdot\hspace{2pt}}^A とは,部分空間 A における閉包を表す。
\overline{V}^A はハウスドルフ空間 X におけるコンパクト集合でもあるから, \overline{V}^A は X における閉集合である。 \overline{V} は, X における V を含む最小の閉集合であるから, \overline{V}^A=\overline{V} でなければならない。特に,
\overline{V}\subset A
である。 V は A における開集合なので,ある X における開集合 W\in\mathcal{O} が存在して,V=A\cap W とかける。よって,
となる。ここで, \overline{A}\cap W\subset \overline{A\cap W} である(※後述)ので,
右辺は x を含む,部分空間 \overline{A} における開近傍であるので, A が開集合であることになる。
※について y\in \overline{A}\cap W とする。 X における y の任意の開近傍 y\in N を取ると, W は開集合なので, y\in W\cap N も開近傍であり,これと y\in \overline{A} から, A\cap W\cap N\ne\emptyset である。これは, y\in \overline{A\cap W} を意味する。したがって, \overline{A}\cap W\subset \overline{A\cap W} である。
証明終
この定理からの帰結である次の系も大切です。
定理5の系
(X,\mathcal{O}) を局所コンパクトハウスドルフ空間( T_2 空間)とし, A\subset X を稠密な部分集合(すなわち \overline{A}=X)とする。このとき,
A が局所コンパクト \iff A が開
である。
証明
\implies について
A が局所コンパクトなら,定理5より,ある開集合 U と閉集合 F を用いて A=U\cap F とかける。
X=\overline{A}=\overline{U\cap F}\subset \overline{U}\cap F
なので, F=X でなければならない。ゆえに, A=U となるので, A は開集合である。
\impliedby について
A が開集合ならば, A= A\cap X の形でかけているので,定理5より, A は局所コンパクトである。
証明終
局所コンパクトハウスドルフ空間には,他にも重要な性質がありますが,それは別の記事が完成次第,追記することにしましょう。
コンパクト性に関するその他の概念
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strongly locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち,各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち,各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |
関連する記事
参考
- 内田伏一「集合と位相」(裳華房 数学シリーズ, 増補新装版, 2020)
- 松坂和夫「集合・位相入門」 (岩波書店 数学入門シリーズ,新装版,2018)
- R. Engelking, General Topology, Revised and completed edition. Sigma Series in Pure Mathematics, 1989.
- J. L. Kelly, General Topology, Springer, 1975.
- L. A. Steen, J. A. Seebach, Counterexamples in Topology, 2nd edition. Springer, 1978.
- S. Willard, General Topology, Dover Publications, 2004.