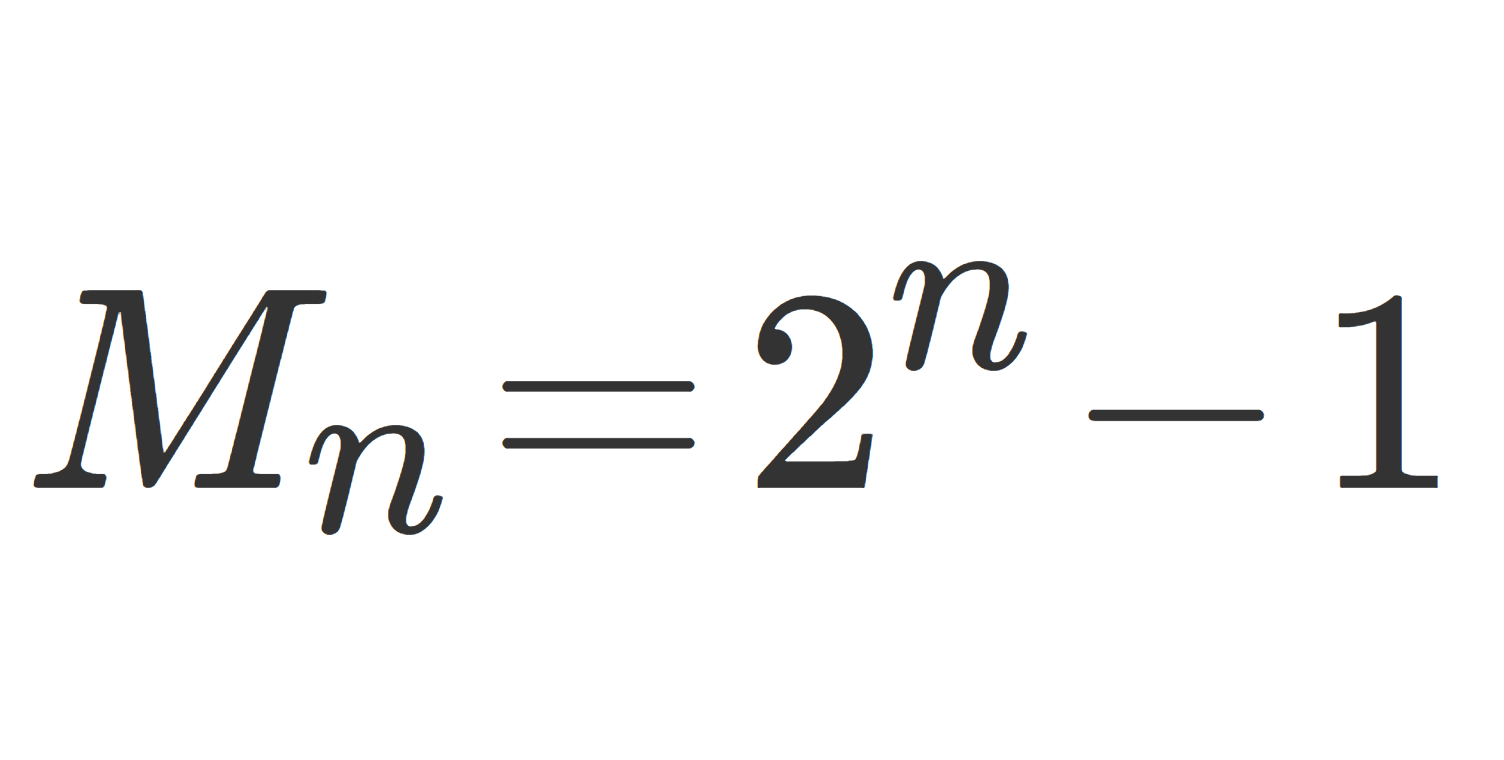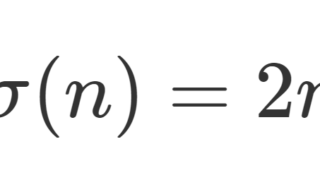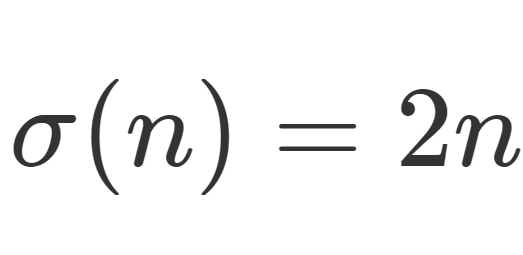メルセンヌ数とは, 2^n-1 と表せる数で,これが素数のときはメルセンヌ素数といいます。これについて,定義と性質を解説しましょう。
メルセンヌ数・メルセンヌ素数とは
定義(メルセンヌ数・メルセンヌ素数)
正の整数 n に対し,
\Large \color{red} M_n=2^n-1
の形の数をメルセンヌ数 (Mersenne number) という。メルセンヌ数が素数であるとき,メルセンヌ素数 (Mersenne prime) という。
メルセンヌ数・メルセンヌ素数の具体例を挙げましょう。
| M_n | 素数か否か | |
|---|---|---|
| 2^1-1 | 1 | |
| 2^2-1 | 3 | 〇 |
| 2^3-1 | 7 | 〇 |
| 2^4-1 | 15 | |
| 2^5-1 | 31 | 〇 |
| 2^6-1 | 63 | |
| 2^7-1 | 127 | 〇 |
| 2^8-1 | 255 | |
| 2^9-1 | 511 | |
| 2^{10}-1 | 1023 | |
| 2^{11}-1 | 2047 |
メルセンヌ素数は現在52個知られており,一番大きい数は 2^{136279841}-1 です。メルセンヌ素数が無数に存在するかどうかは未解決問題です。
メルセンヌ数・メルセンヌ素数の性質
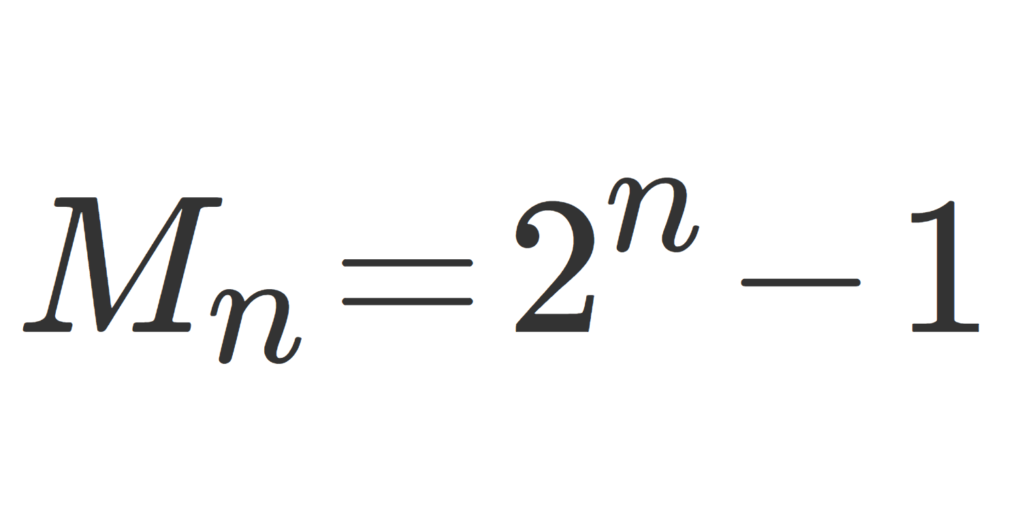
メルセンヌ数が素数ならばnは素数
M_n = 2^n-1 が素数ならば n は素数であることが分かります。より一般に, a^n-1 が素数ならば a=2 かつ n は素数です。主張を述べましょう。
定理(メルセンヌ数が素数ならば指数は素数)
a,n を 2 以上の整数とする。 a^n-1 が素数ならば, a=2 かつ n は素数である。
証明
a^n - 1 = (a-1)(a^{n-1}+a^{n-2}+\dots + 1)
である。 a^{n-1}+a^{n-2}+\dots + 1 >1 であることと,これが素数であることから,a-1=1 すなわち a=2.
n\ge 2 が素数でないと仮定すると, n=pq \;\; (p,q\in \mathbb{Z}_{\ge 2} ) と表せる。このとき,
\!\! 2^{pq} - 1 = (2^p-1)(2^{p(q-1)}+2^{p(q-2)}+\dots + 1)
であり, 2^p-1, 2^{p(q-1)}+2^{p(q-2)}+\dots + 1>1 より,素数であることに矛盾する。よって,n は素数である。
証明終
メルセンヌ素数と完全数との関係
正の整数 n が完全数 (perfect number) であるとは, n の,自分自身以外の正の約数の総数が n となる数のことを指します。このとき,以下の定理が成立します。
定理(メルセンヌ素数と完全数)
- メルセンヌ数 M_n = 2^n-1 が素数ならば 2^{n-1} M_n = 2^{n-1}(2^n-1) は完全数である。
- 偶数の完全数はあるメルセンヌ素数 M_n を用いて 2^{n-1}M_n = 2^{n-1}(2^n-1) とかける。
これは以下で証明しています。