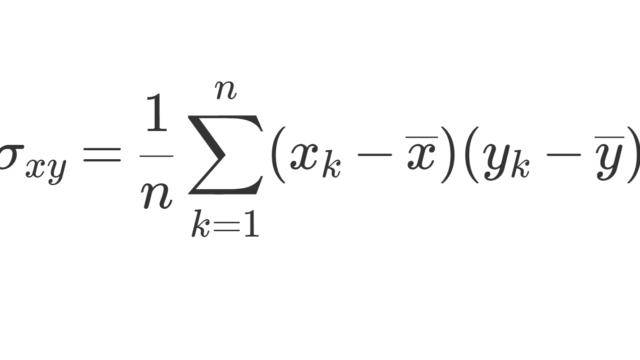 統計学
統計学 データの共分散の定義と求め方の具体例・性質
データにおける共分散 (covariance) ついて定義を詳しく述べ,求め方の具体例から性質までを証明付きで順番に述べましょう。
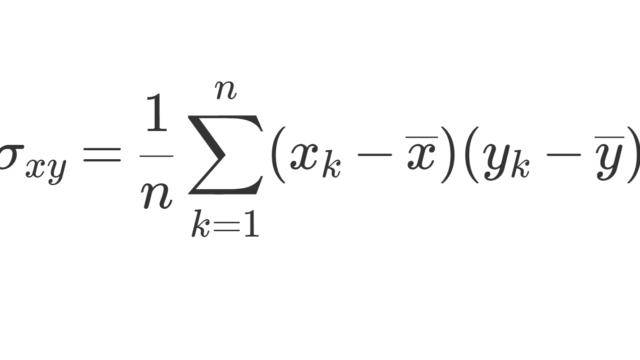 統計学
統計学 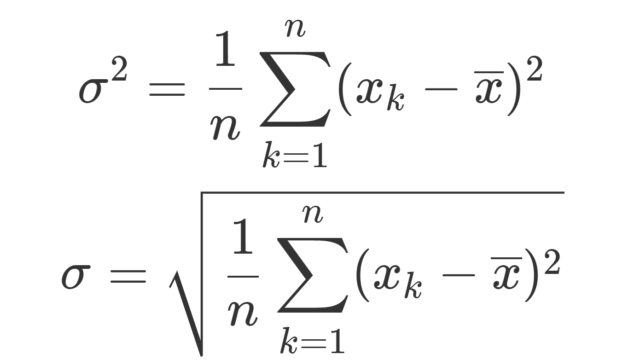 統計学
統計学 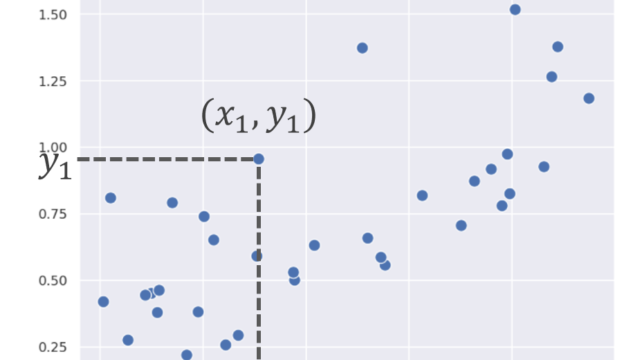 統計学
統計学 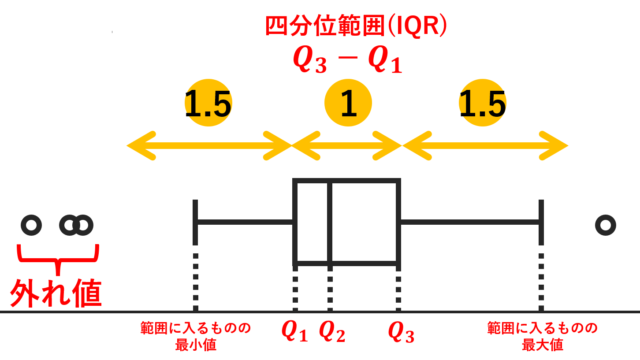 統計学
統計学 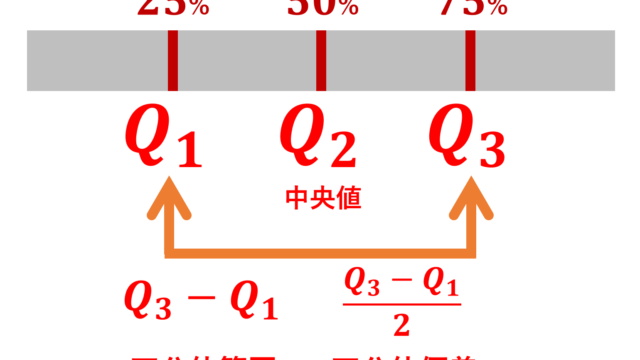 統計学
統計学 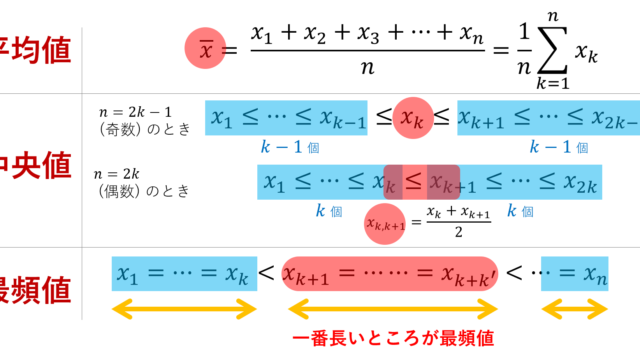 統計学
統計学 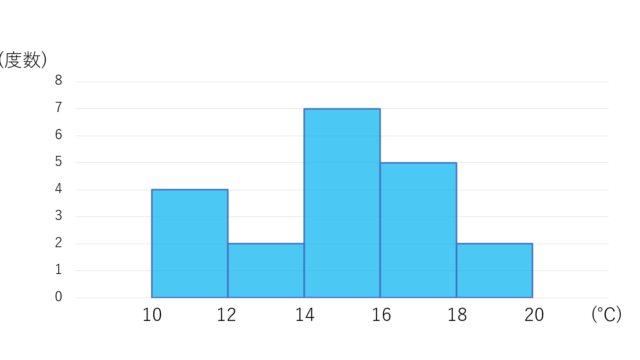 統計学
統計学 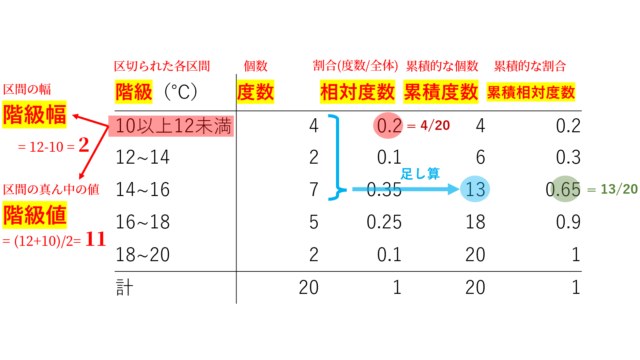 統計学
統計学  群・環・体
群・環・体 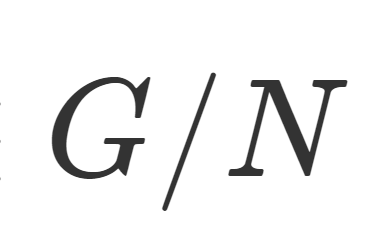 群・環・体
群・環・体