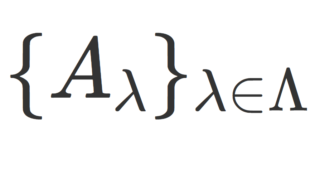べき集合とは何かをわかりやすく～定義と具体例と性質～

大学数学において，「べき集合」は詰まりやすい概念の1つでしょう。一言でいうと，べき集合とは，ある集合の部分集合全体の集合を指します。これについて，その定義を，具体例を交えてわかりやすく解説し，最後に性質も述べます。

べき集合の定義
べき集合の具体例
べき集合の性質3つ
おわりに
関連する記事

べき集合の定義

定義（べき集合）

$A$ を集合とする。このとき，

\color{red}2^A = \{ E \mid E\subset A\}

を $A$ のべき集合 (冪集合；巾集合；power set) という。べき集合は $\color{red} 2^A$ の他， $\color{red} \mathcal{P}(A)$ や $\color{red} \mathfrak{P}(A)$ などと書かれることがある。

$\mathcal{P},\mathfrak{P}$ はそれぞれ，カリグラフィー，フラクトゥールのPです。

$A$ の部分集合全体の集合をべき集合というのですね。

そもそも「集合を要素にもつ集合」というものを考えたことがないかもしれません。高校生のうちは， $\{1,2,3\}$ のように，集合の要素は「数」であることが多いでしょう。
しかし，別に集合の要素が集合であっても構いません。たとえば， $A,B,C$ を集合としたときに， $\{A,B,C\}$ のような，集合を要素にもつ新たな集合を考えてもいい訳です。

これを踏まえて，具体例を確認していきましょう。

べき集合の具体例

まずは図で考えてみましょう。以下のような，要素を2つ持つ集合を考えます。

これの部分集合は以下の4つですよね。（空集合や，元の集合そのものも部分集合になることに注意）

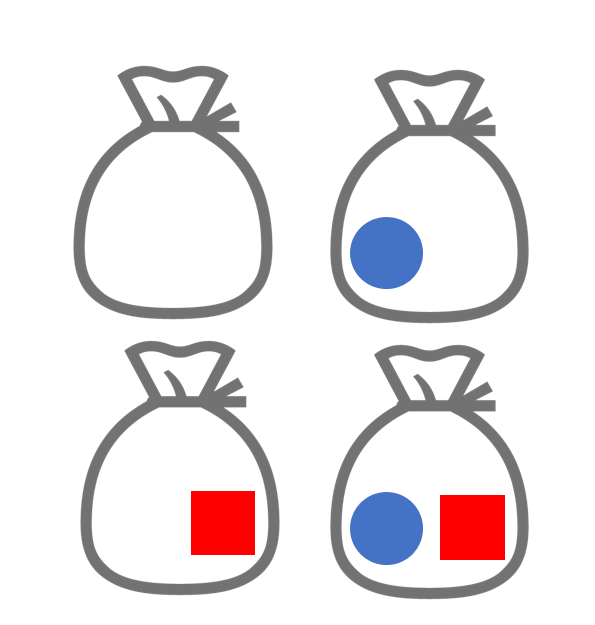
よって，これらを新たな「袋」に入れた以下の１つの大きな集合が，べき集合になります。

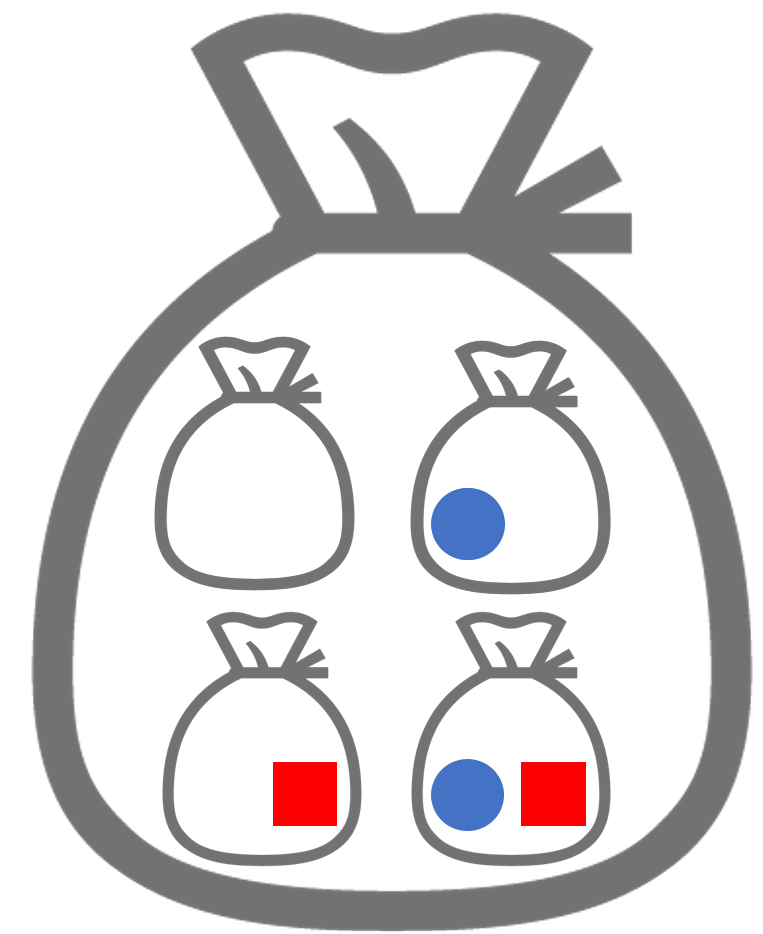
このイメージを，実際に以下の例1で，確認してみましょう。

例1

$A= \{a,b\}$ のべき集合は

2^A = \Bigl\{ \emptyset, \{a\}, \{b\}, \{a,b\}\Bigr\}

である。

さっきのイメージ図通り， $A$ の部分集合は $\emptyset, \{a\}, \{b\}, \{a,b\}$ の4つですから，その4つを要素にもつ集合が，べき集合になるわけですね。

さて，次は集合の要素数を増やしてみましょう。

例2

$B=\{a,b,c\}$ のべき集合は

\begin{aligned}2^B=&\Bigl\{\emptyset,\{a\}, \{b\}, \{c\}, \\ & \{a,b\}, \{b,c\}, \{a,c\}, \{a,b,c\}\Bigr\} \end{aligned}

である。

$B$ の部分集合は $\emptyset,\{a\}, \{b\}, \{c\}, \{a,b\}, \{b,c\}, \{a,c\}, \{a,b,c\}$ の8つですから，その8つを要素にもつ集合が，べき集合になります。

さて次は，空集合のべき集合について，考えてみましょう。

例3

$C=\emptyset$ に対し，

\begin{aligned}2^C &= \{\emptyset\}, \\ 2^{(2^C)} &= \bigl\{\emptyset, \{\emptyset\}\bigr\}, \\ 2^{(2^{(2^C)})}&= \Bigl\{\emptyset, \{\emptyset\}, \bigl\{\{\emptyset\}\bigr\}, \bigl\{\emptyset, \{\emptyset\}\bigr\} \Bigr\}\end{aligned}

である。

空集合のべき集合を考えるにあたっては，空集合という集合を部分集合に持つと考えます。 $\emptyset$ の部分集合は $\emptyset$ のみですから，べき集合は，この空集合を「袋」に入れて $\{\emptyset \}$ となるわけです。これは，要素数が $1$ 個の集合です。（空集合は要素数が $0$ 個の集合です。）

さらにこの集合のべき集合 $2^{(2^C)}$ を考えるときは， $\{\emptyset \}$ から何も取らない部分集合 $\emptyset$ と，集合全体をとると考える部分集合 $\{\emptyset \}$ の2つがあると考え，それを大きな「袋」に入れた $\{ \emptyset, \{\emptyset \}\}$ がべき集合になります。以下同様です。