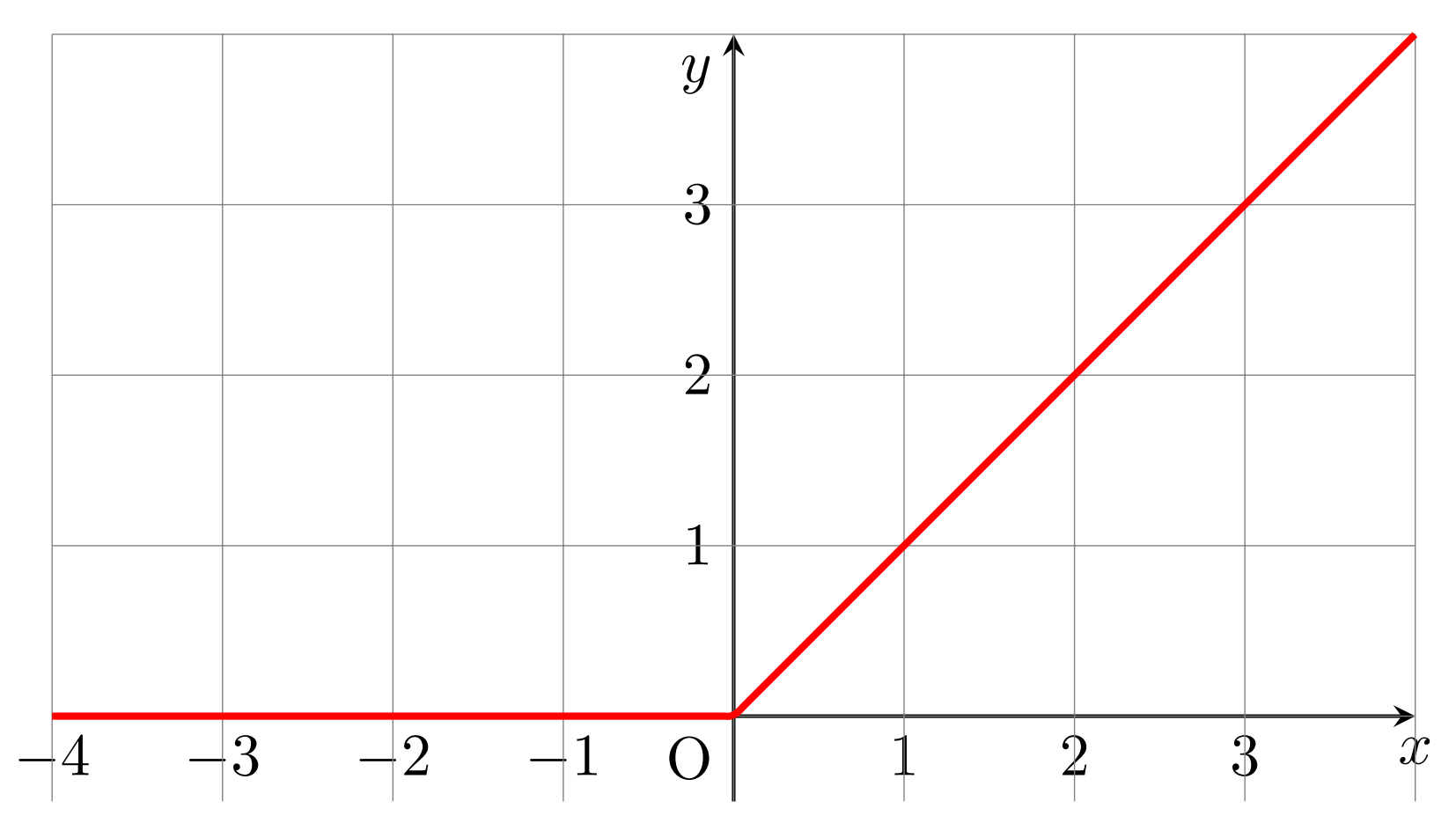
ReLU関数(ランプ関数,正規化線形関数)とは

ReLU関数 (Rectified Linear Unit)，より一般に「ランプ関数 (ramp function)」「正規化線形関数」とは， $x\ge 0$ のとき $x$ ， $x < 0$ のとき $0$ となる関数のことです。この関数の定義とグラフ，その性質を述べましょう。

ReLU関数(ランプ関数,正規化線形関数)の定義

定義（ReLU関数；ランプ関数；正規化線形関数）

\color{red}f(x) = \begin{cases} 0 & \text{if }x < 0, \\ x & \text{if } x \ge 0 \end{cases}

をReLU関数 (Rectified Linear Unit)，あるいはランプ関数 (ramp function) や正規化線形関数 (Rectified linear function) ともいう。

関数の定義自体は単純ですね。

ReLU関数と呼ばれるのは，ニューラルネットワークにおける，活性化関数のニュアンスで使うときです。

なお，この関数は以下のように表現しても同じです。

ReLU関数の別表現

\color{red}\begin{aligned} f(x) &= \begin{cases} 0 & \text{if }x < 0, \\ x & \text{if } x \ge 0 \end{cases} \\ &= \max\{0, x\} \\ &= \frac{x+|x|}{2}. \end{aligned}

ReLU関数のグラフを述べましょう。これは，以下のようになります。

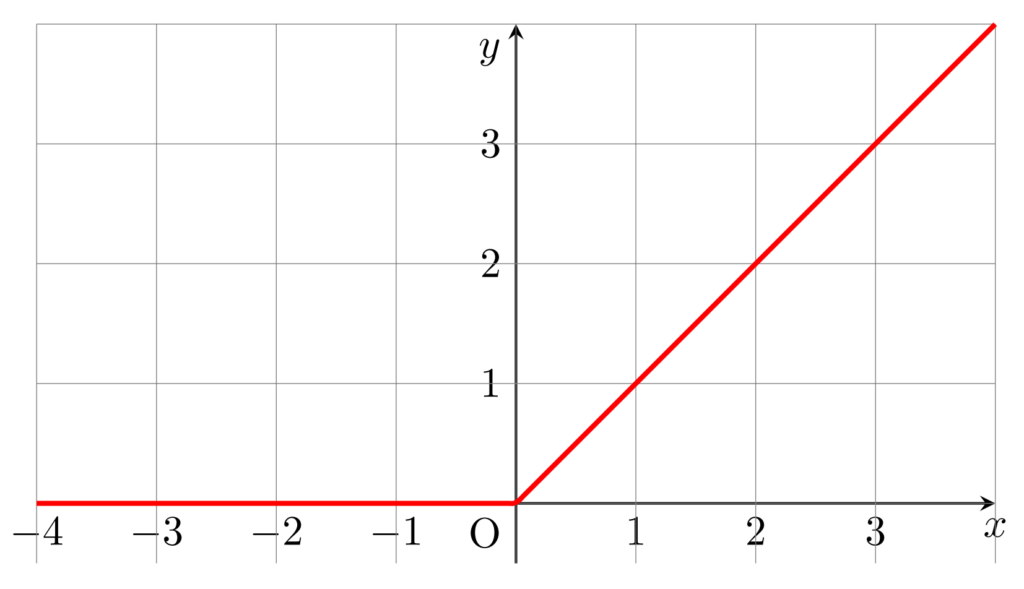
非常に単純な形ですね。ニューラルネットワークでは，「線形でない」すなわち直線でないという点が，活性化関数として重要です。

ReLU関数(ランプ関数,正規化線形関数)の基本的な性質を列挙しておきましょう。

命題（ReLU関数の性質）

$f\colon \mathbb{R} \to \mathbb{R}$ をReLU関数とする。このとき，

1. $f(x) \ge 0 .$

2. $f'(x) = \begin{cases} 0 & x < 0, \\ 1 & x>0.\end{cases}$
特に，微分はステップ関数になる。

3. $\displaystyle \int_0^\infty e^{-tx} f(x)\, dx = \frac{1}{t^2} \;\;(t>0).$ （ラプラス変換）