 微分積分学(大学)
微分積分学(大学) 上に有界な単調増加数列は収束することの証明
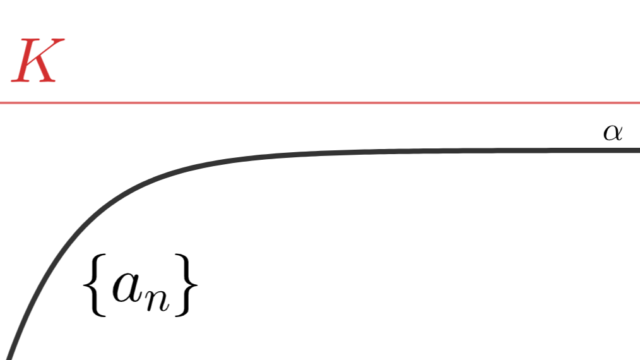
「上に有界な単調増加数列」あるいは「下に有界な単調減少数列」は収束するという定理は,高校数学で証明なしに用いた定理の1つでしょう。これは,実数の連続性と数列の極限を厳密に定義するε-N論法を用いて証明されます。これについて証明しましょう。
 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)