 微分積分学(大学)
微分積分学(大学) 平均値の定理・ロルの定理とその証明
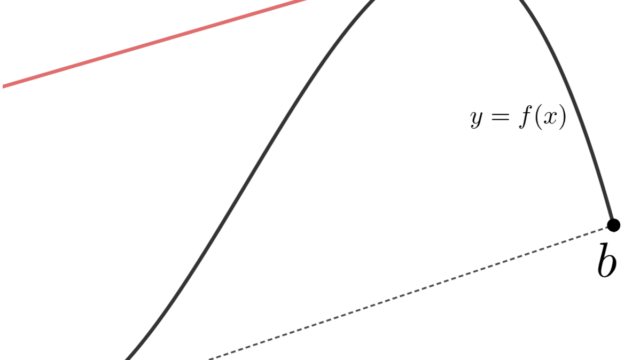
高校理系数学や大学教養数学(微分積分学)に登場する,平均値の定理 (mean value theorem) と,その準備としてロルの定理 (Rolle's theorem) をわかりやすく紹介し,それぞれの証明を行います。
 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 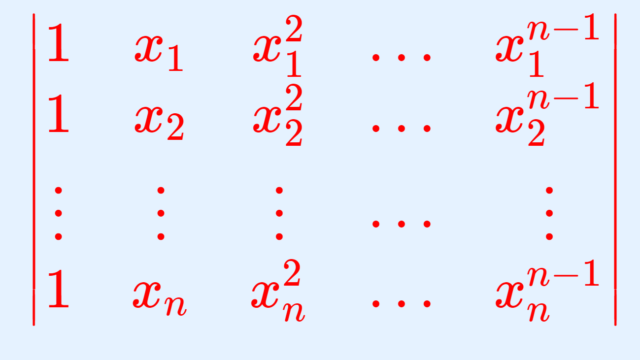 線形代数学
線形代数学 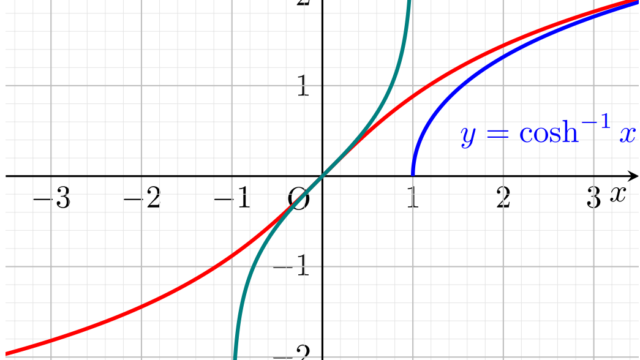 微分積分学(大学)
微分積分学(大学) 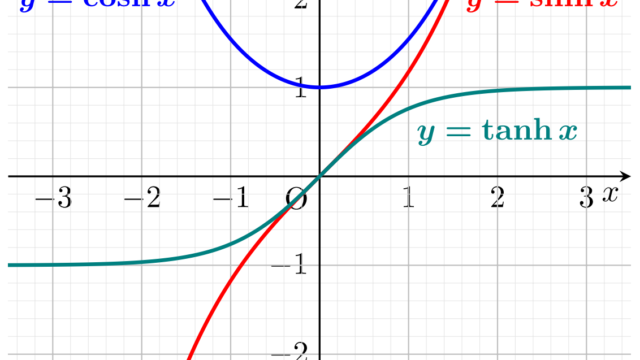 微分積分学(大学)
微分積分学(大学) 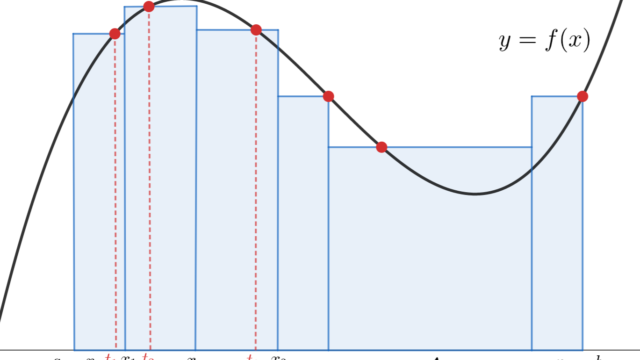 微分積分学(大学)
微分積分学(大学) 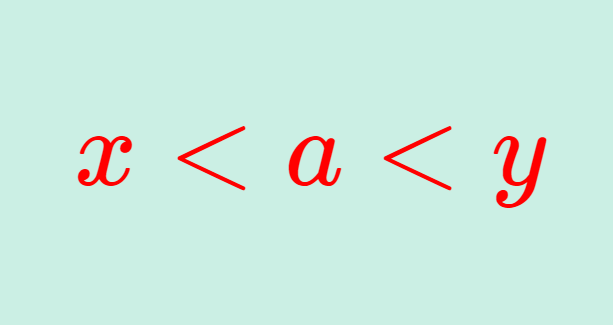 微分積分学(大学)
微分積分学(大学) 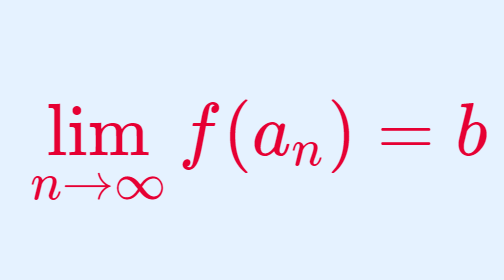 微分積分学(大学)
微分積分学(大学)