チコノフの定理とその証明～コンパクトな直積はコンパクト～

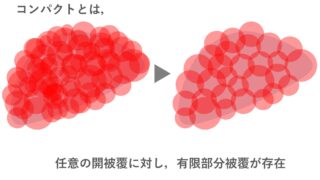
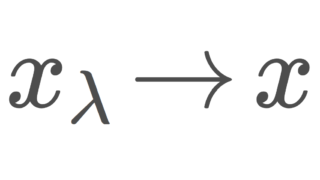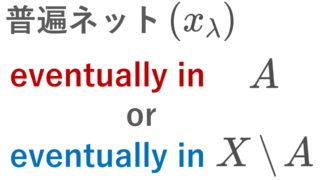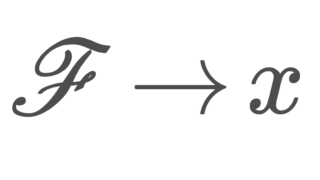チコノフの定理とは，コンパクトな空間の直積はコンパクトであるという定理です。選択公理が必要な定理で，普通に証明しようとすると複雑ですが，ネット(有向点族)あるいはフィルターの概念を認めると簡単に証明できます。

本記事では，ネット(有向点族)・フィルターの概念を認めて証明しましょう。

チコノフの定理

チコノフの定理 (Tychonoff’s theorem)

$\Alpha$ を空でない集合とし，各 $\alpha\in\Alpha$ に対し， $(X_\alpha, \mathcal{O}_\alpha)$ は位相空間とする。

このとき，直積空間 $X=\prod_{\alpha\in\Alpha} X_\alpha$ がコンパクトである必要十分条件は，各 $X_\alpha$ がコンパクトであることである。

$\implies$ の証明は簡単です。 $p_\alpha\colon X\to X_\alpha$ を自然な射影とすると， $p_\alpha$ は連続であり，コンパクト集合の連続像はコンパクトであるから， $X$ がコンパクトならば $X_\alpha$ もコンパクトです。

チコノフの定理は選択公理と同値な命題として知られています。まあ位相空間の多くの議論は，選択公理を無意識に使っていることもありますから，今さら強調して言うことではないのかもしれませんがね。

$\impliedby$ の証明をしましょう。ネット(有向点族)あるいはフィルターの知識を認めると，ものすごく簡単に証明できるので，今回はネット(有向点族)を使った証明と，フィルターを使った証明を紹介しましょう。

普遍ネット(超ネット)を用いると簡単に証明できます。

$\impliedby$ のネットによる証明

$(x_\lambda)\subset X$ を普遍ネットとする。普遍ネットの像は普遍ネットなので， $\bigl(p_\alpha(x_\lambda)\bigr)$ は $X_\alpha$ 上の普遍ネットである。

$X_\alpha$ はコンパクトであり，コンパクト空間上の普遍ネットは収束するので， $p_\alpha(x_\lambda)\to x_\alpha$ となる $x_\alpha\in X_\alpha$ が存在する。

このとき， $x=(x_\alpha)\in X$ とおくと，直積位相とネットの収束の関係により， $x_\lambda\to x$ である。 $X$ 上の任意の普遍ネットが収束するので， $X$ はコンパクトである。

証明終

普遍ネット(超ネット)の概念をとらえるのに，選択公理を用いています。

フィルターの知識はあるものとします。

$\impliedby$ のフィルターによる証明

$\mathscr{F}$ を $X$ 上の超フィルターとする。超フィルターの像は超フィルターなので， $p_\alpha(\mathscr{F})$ は $X_\alpha$ 上の超フィルターである。

$X_\alpha$ はコンパクトであり，コンパクト空間上の超フィルターは収束するので， $p_\alpha(\mathscr{F})\to x_\alpha$ となる $x_\alpha\in X_\alpha$ が存在する。

このとき， $x=(x_\alpha)\in X$ とおくと，直積位相とフィルターの収束の関係より， $\mathscr{F}\to x$ である。 $X$ 上の任意の超フィルターが収束するので， $X$ はコンパクトである。

証明終

超フィルターの概念をとらえるのに，選択公理を用いています。

ネット(有向点族)やフィルターを使わない証明もあり，それはたとえば内田伏一「集合と位相」や松坂和夫「集合・位相入門」には載っていますが，証明は長いです。正直，ネット(有向点族)やフィルターを使わない証明を理解するのに労力を使うくらいなら，ネット(有向点族)あるいはフィルターを学ぶ労力に回した方が良いと考えます。もちろん，ネット(有向点族)やフィルターを使わない証明を大した労力なく理解できる人もいるので，それを否定するわけではありません。