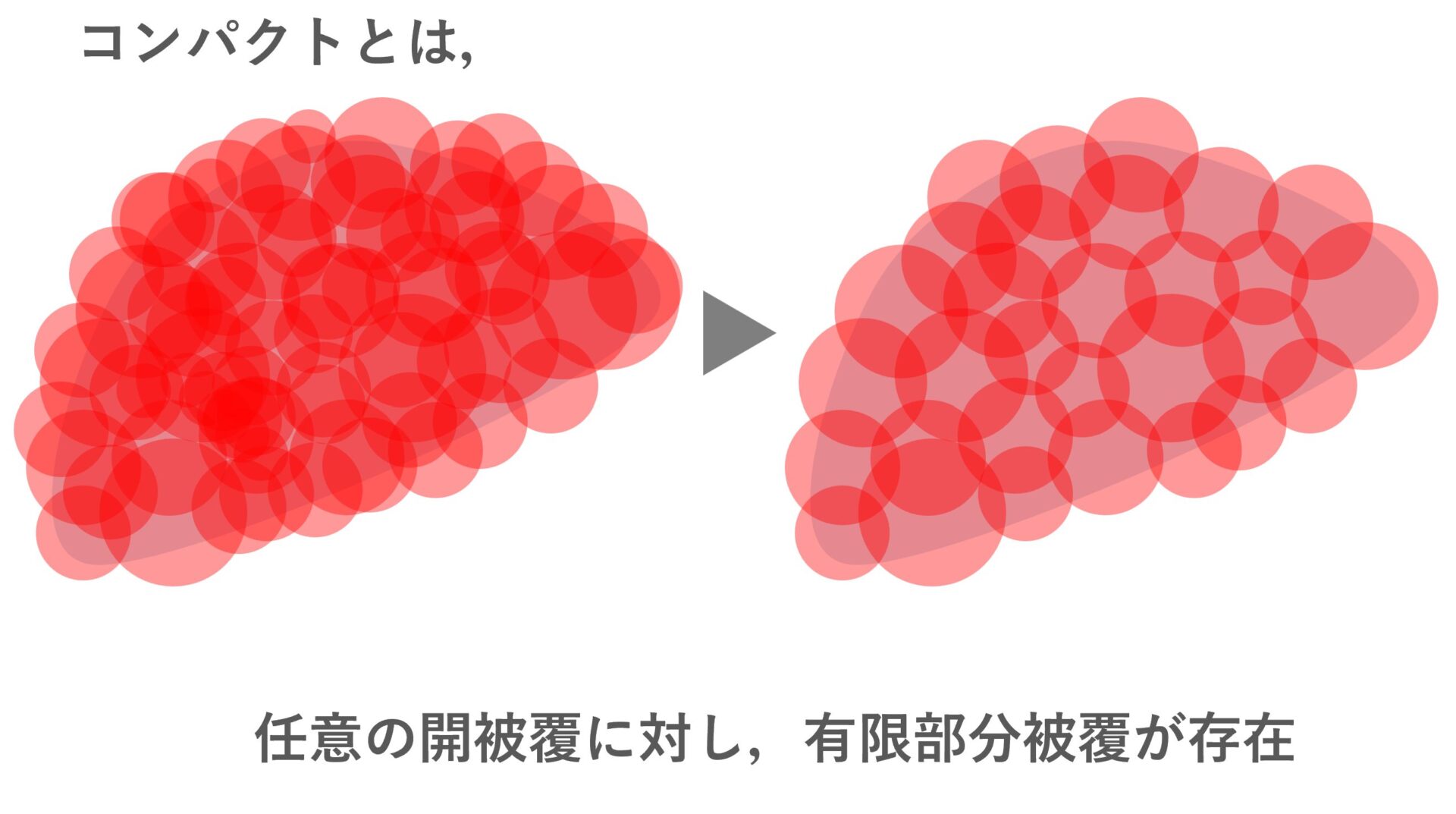
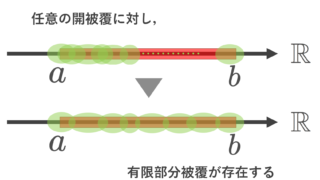
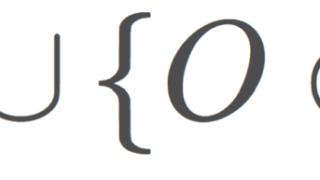位相空間におけるコンパクト集合とは，任意の開被覆に対し，その有限部分被覆が存在することを言います。
コンパクト性はある意味「コンパクト」にまとまった空間で，大雑把には，日常会話で使う「コンパクト」のイメージをそのまま持って構いません。性質が良く，たとえばコンパクト集合上の実連続関数は，最大値と最小値をもちます。紹介していきましょう。
コンパクト集合・コンパクト空間の定義
まず準備として，開被覆や有限部分被覆の定義をしてから，コンパクトの定義をしましょう。
開被覆・有限部分被覆
\mathcal{C} と C の字の使い分けに注意してください。
定義1（開被覆）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。また， \mathcal{C}\subset 2^X を部分集合族とする(2^X はべき集合)。
\Large\color{red} A\subset \bigcup_{C\in \mathcal{C}} C
が成り立つとき， \mathcal{C} は A を被覆するといい， \mathcal{C} は A の被覆 (covering) であるという。
\mathcal{C}\subset\mathcal{O} すなわち， \mathcal{C} の元が開集合であるとき， \mathcal{C} は A の開被覆 (open covering) であるという。
さらに，\mathcal{C}_0\subset \mathcal{C} も A を被覆する，すなわち A\subset \bigcup_{C\in \mathcal{C}_0} C が成り立つとき， \mathcal{C}_0 は \mathcal{C} の部分被覆 (subcovering) であるという。\mathcal{C}_0 が有限集合である( \mathcal{C}_0 に属する集合が有限個である)とき，\mathcal{C}_0 は有限部分被覆 (finite subcovering) であるという。
A を被覆するとは，和集合が A を覆っているということですね。これをもとにコンパクトの定義をしましょう。
コンパクト集合・コンパクト空間の定義
定義2（コンパクト空間とコンパクト集合）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。また， \mathcal{C}\subset 2^X を部分集合族とする(2^X はべき集合)。
A の任意の開被覆 \mathcal{C} に対し，有限部分被覆 \mathcal{C}_0\subset \mathcal{C} が存在するとき， A をコンパクト集合 (compact set) であるという。
さらに， X 自体がコンパクト集合であるとき， (X,\mathcal{O}) はコンパクト空間 (compact space) であるという。
簡単に言うと， A のどんな開被覆を取ってきても，実はそのうちの有限個の集合で覆えているよということです。「どんな開被覆でも」というのがポイントで，たとえば， \{X\} は，任意の集合 A\subset X の開被覆になっていますが，だから任意の集合はコンパクトということにはなりません。開被覆の取り方を変えると，有限個で覆えていないかもしれないからです。一つでも有限個で覆えない A の開被覆が取ってこれれば，A はコンパクトではありません。
ここで，部分集合のコンパクト性を考えるにあたって，全体空間でコンパクトを考えているか，部分空間の相対位相でコンパクトを考えているかは，どっちで考えても変わりありません。
定理1（コンパクト集合と相対位相としてのコンパクト空間の一貫性）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。次の2つは同値。
- A は (X,\mathcal{O}) におけるコンパクト集合
- (A, \mathcal{O}_A) はコンパクト空間。ただし， (A, \mathcal{O}_A) は (X,\mathcal{O}) の部分位相空間とする
O\in \mathcal{O} と O\cap A\in\mathcal{O}_A を対応付けることで，簡単に証明できます。
証明
1.\implies 2.について
\mathcal{C}_A\subset \mathcal{O}_A を A の (A, \mathcal{O}_A) における開被覆とする。このとき，各 C_A\in\mathcal{C}_A に対し， C_A= C\cap A となる C\in \mathcal{O} が存在する。
\mathcal{C}=\{C\in\mathcal{O}\mid C\cap A\in\mathcal{C}_A\}
とすると，\mathcal{C} は A の (X, \mathcal{O}) における開被覆である。
A は (X, \mathcal{O}) におけるコンパクト集合なので，有限部分被覆 \mathcal{C}'\subset \mathcal{C} が存在する。このとき，\mathcal{C}'_{A}= \{ C\cap A\mid C\in \mathcal{C}'\}\subset \mathcal{C}_A は， A の \mathcal{C}_A についての有限部分被覆になっているため，示された。
2.\implies 1.について
\mathcal{C}\subset \mathcal{O} を A の (X, \mathcal{O}) における開被覆とする。\mathcal{C}_A= \{ C\cap A\mid C\in\mathcal{C}\} とすると，これは A の (A, \mathcal{O}_A) における開被覆である。
(A, \mathcal{O}_A) はコンパクト空間なので，有限部分被覆 \mathcal{C}'_A\subset \mathcal{C}_A が存在する。\mathcal{C}_A の定義により， C_1, \ldots, C_n\in\mathcal{C} を用いて，
\mathcal{C}'_A=\{ C_1\cap A,\ldots, C_n\cap A\}
とかける。\mathcal{C}'=\{C_1,\ldots, C_n\} は A の \mathcal{C} についての有限部分被覆となっているから，示せた。
証明終
なお文献によっては，コンパクト性の定義に，ハウスドルフ性を加えることもあります。
コンパクト集合・コンパクト空間の具体例
例1( \R).
\R は通常の位相について，コンパクト空間ではない。また， a<b に対し，開区間 (a,b) はコンパクト集合でないが，閉区間 [a,b] はコンパクト集合である。
たとえば，
\R = \bigcup_{n=-\infty}^\infty (n, n+2)
なので， \{ (n, n+2)\}_n は開被覆ですが，ここから有限個を持ってきても，和集合が \R 全体になることはないので， \R はコンパクトではありません。また， (a,b) もコンパクトではありません。なぜなら，
なので， \{ (a, b-1/n)\}_n は開被覆ですが，ここから有限個を持ってきても， (a,b) は覆えないからです。一方で， [a,b] はコンパクトになります。これはハイネ–ボレルの被覆定理といいます。ハイネ–ボレルの被覆定理とその証明～有界閉区間のコンパクト性～で証明しています。
一般に， \R^n の部分集合がコンパクトになる必要十分条件は，それが有界閉集合になることです。これは， M>0 に対し，後の定理2.6から， [-M, M]^n がコンパクトになることと，後の定理2.2より分かります。たとえば，円周 S^1=\{ (x,y)\in\R^2\mid x^2+y^2=1\} はコンパクトです。
例2(密着空間・離散空間).
密着空間 (X, \{ \emptyset, X\}) は，任意の部分集合がコンパクトである。特に密着空間はコンパクト空間である。
離散空間 (X, 2^X) の部分集合 A\subset X がコンパクトになる必要十分条件は， A が有限集合であることである。
密着空間における開被覆は \{X\} しかないので，任意の開被覆が有限被覆です。よって，コンパクトです。
離散空間は，全ての1点集合が開集合です。よって， \mathcal{C}=\bigl\{\{a\} \mid a\in A\bigr\} とおくと，\mathcal{C} は開被覆になり，A=\bigcup_{C\in\mathcal{C}}C です。さらに， \mathcal{C} の中の元が一つでも欠けると， A を被覆しないので， \mathcal{C} そのものが有限集合であるかどうかで， A がコンパクトかが決まります。
より一般に， \mathcal{O}_1\subset \mathcal{O}_2 を X 上の位相としたときに， (X,\mathcal{O}_2) における部分集合 A\subset X がコンパクトならば， A は (X,\mathcal{O}_1) においてもコンパクトになります。なぜなら， (X,\mathcal{O}_1) における開被覆は， (X,\mathcal{O}_2) における開被覆でもあるため， (X,\mathcal{O}_2) のコンパクト性から，有限部分被覆が取ってこれるからです。
コンパクト性とは，位相空間が小さい（粗い・弱い）ほど，成り立ちやすい性質です。
例3(有限部分集合).
(X, \mathcal{O}) を位相空間とする。このとき，任意の有限部分集合はコンパクトである。
例2.で，離散位相上で有限部分集合がコンパクトであることと，例2.で述べたように， \mathcal{O}_1\subset \mathcal{O}_2 を X 上の位相としたときに， (X,\mathcal{O}_2) における部分集合 A\subset X がコンパクトならば， A は (X,\mathcal{O}_1) においてもコンパクトになることから，直ちに従います。
もう少し非自明で，かつ確認が簡単な例を考えましょう。
例4(補有限位相).
X を空でない集合とし，
\mathcal{O} =\{ O\subset X\mid X\setminus O\text{ is finite}\}
を，補集合が有限集合となる部分集合族とすると， (X,\mathcal{O}) は位相空間となる。この空間はコンパクト空間である。
\mathcal{C} を開被覆とし， C\in\mathcal{C} を一つ取ります。このとき， X\setminus C は有限集合なので， X\setminus C=\{x_1, \ldots, x_n\} とかけます。 x_1\in C_1, \ldots, x_n \in C_n となる C_1, \ldots, C_n \in\mathcal{C} を取ると，\mathcal{C}_0 =\{C, C_1, \ldots, C_n\} は有限部分被覆となっており，コンパクト性が示せました。
例5(除外点位相).
X を空でない集合とし， x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\notin O\}\cup \{X\}
を， x を含まない部分集合族(と \{X\} の和集合)とすると， (X,\mathcal{O}) は位相空間となる。この空間はコンパクト空間である。
x\in X を含む開集合は， X しかないので， X の開被覆 \mathcal{C} は \{X\}\subset \mathcal{C} となります。有限部分被覆が取れたので， X はコンパクトです。
なお， X\setminus\{x\} は離散空間になりますから， X が無限集合のときは， X\setminus\{x\} はコンパクトにはなりません。これは，コンパクト空間でも，その部分集合はコンパクトとは限らないことを示しています（これ自体は，たとえば， (0,1)\subset[0,1] などでも示せます）。ちなみに，コンパクト空間の閉部分集合はコンパクトになります。後の定理2.2で紹介します。
例6(特定点位相).
X を無限集合とし， x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\in O\}\cup \{\emptyset\}
を， x を含む部分集合族(と \{\emptyset\} の和集合)とすると， (X,\mathcal{O}) は位相空間となる。
このとき，\{x\} は1点集合なのでコンパクトであるが，その閉包 \overline{\{x\}}=X はコンパクトでない。
これは，部分集合 A がコンパクトでも，その閉包 \overline{A} はコンパクトとは限らないことを示しています。
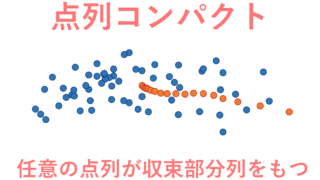
点列コンパクト (sequentially compact) とは，任意の点列 \{ a_n\}\subset A が， A 内の元に収束する部分列を含むことを言います。
これについては，いずれ別の記事で証明しましょう。
コンパクト集合・コンパクト空間の性質
以下は，コンパクトにおける重要かつ基本的な性質たちです。
定理2（コンパクト空間の性質）
順番に証明していきましょう。
2.1 コンパクト集合の有限個の和集合はコンパクトであること
(X,\mathcal{O}) を位相空間とし， A_1, A_2,\ldots, A_n\subset X をコンパクトとするとき， B=A_1\cup A_2\cup\cdots \cup A_n もコンパクトであることを示しましょう。
証明
\mathcal{C} を B の開被覆とする。 A_1\subset B なので， \mathcal{C} は A_1 の開被覆でもある。 A_1 はコンパクトより，有限部分被覆 \mathcal{A}_1\subset \mathcal{C} が存在する。
同様に， A_2,\ldots, A_n の有限部分被覆 \mathcal{A}_2,\ldots, \mathcal{A}_n も存在し，\mathcal{B}=\bigcup_{k=1}^n \mathcal{A}_k とすると，これは，B の被覆になっている。\mathcal{B} は \mathcal{C} の有限部分被覆となるから， B はコンパクトである。
証明終
2.2 コンパクト空間の閉部分集合がコンパクトであること
(X,\mathcal{O}) をコンパクト空間とし， A\subset X を閉部分集合とするとき， A がコンパクトであることを示しましょう。
証明
\mathcal{C} を A の開被覆とする。このとき， A^c は開集合だから， \mathcal{C}\cup \{A^c\} は X の開被覆となる。 X はコンパクトなので，有限部分被覆 \mathcal{C}_0 が存在する。 \mathcal{C}_0\setminus \{A^c\}\subset \mathcal{C} は A の有限部分被覆になっていなければおかしいので，題意は示された。
証明終
\mathcal{C}\cup \{A^c\} は X の開被覆となっていることがポイントです。
2.3 ハウスドルフ空間のコンパクト集合は閉集合であること
(X,\mathcal{O}) をハウスドルフ空間とし， A\subset X をコンパクトとしたとき， A が閉集合になることを示しましょう。
証明
x\in X\setminus A とする。このとき， \mathcal{C}=\{ O\in \mathcal{O}\mid x\notin \overline{O}\} は A の開被覆になる。なぜなら， X はハウスドルフ空間より，各点 a\in A に対し， a\in O かつ x\notin \overline{O} となる O\in\mathcal{O} が存在するからである。
A はコンパクトなので，有限個の集合 C_1, C_2,\ldots, C_n \in \mathcal{C} が存在して，
A\subset C_1\cup C_2\cup \cdots \cup C_n
とできる。両辺閉包を取ると，【位相空間】閉包とは～定義と例と性質～で解説した通り，
となる。右辺は x を含まないので， x\notin \overline{A} となる。任意の x\in X\setminus A でそうなるから，A は閉集合である。
証明終
2.4 コンパクト集合の連続写像の像もコンパクトであること
(X,\mathcal{O}_X),(Y, \mathcal{O}_Y) を位相空間とし， f\colon X\to Y を連続とする。 A\subset X をコンパクトとするとき，その像 f(A)\subset Y もコンパクトである
これを証明しましょう。
証明
\mathcal{C}\subset \mathcal{O}_Y を f(A) の開被覆とすると， f は連続より， \{ f^{-1}(C)\mid C\in\mathcal{C}\} は A の開被覆となる。A はコンパクトより，有限部分被覆 \{f^{-1}(C_1), \ldots, f^{-1}(C_n)\} が存在する。すなわち，
A\subset f^{-1}(C_1)\cup \cdots \cup f^{-1}(C_n)
となるが，両辺 f で送ると，写像の像・逆像と集合との演算証明より，
となる。したがって， f(A) もコンパクトである。
証明終
2.5 コンパクト空間上の実連続関数は最大値と最小値をもつこと
(X,\mathcal{O}_X) をコンパクト空間とし， f\colon X\to \R を連続としたときに，最大値と最小値を持つことを示しましょう。
証明
定理2.4より， f(X)\subset \R はコンパクトである。例1.で述べたように， f(X) は有界閉集合であるから，最大値と最小値をもつ。
証明終
2.6 コンパクト空間の直積空間はコンパクトであること
\{(X_\lambda, \mathcal{O}_\lambda)\}_{\lambda\in\Lambda} をコンパクト空間の族とすると，その直積空間 \prod_{\lambda\in\Lambda} X_\lambda もコンパクトである
これはチコノフの定理 (Tychonoff’s theorem) と呼ばれ，証明には選択公理が必要です。有限個の直積の場合は，選択公理は不要ですので，ここでは有限個に限って証明することにしましょう。2個の直積について言えれば，帰納的に n 個の直積についても言えるので，2個の場合を示します。具体的には，以下を示しましょう。
(X,\mathcal{O}_X),(Y, \mathcal{O}_Y) をコンパクト空間とするとき，その直積空間 X\times Y もコンパクトである。
証明には，射影 p\colon X\times Y \ni (x,y)\mapsto x\in X と q\colon X\times Y \ni (x,y)\mapsto y\in Y を用います。
有限個の場合の証明
\mathcal{C} を X\times Y の被覆とする。 x\in X とし，
\mathcal{C}_x = \{ C\in\mathcal{C}\mid x\in p(C)\}
とする。\mathcal{C} は X\times Y の開被覆より，q(\mathcal{C}_x) = \{ q(C_x)\mid C_x\in\mathcal{C}_x\} は Y の開被覆である(射影は開写像であることに注意)。
Y はコンパクトより，有限部分被覆 \{ q(C_{x,1}),\ldots, q(C_{ x, n_x})\}\subset q(\mathcal{C}_x) があって，
Y = q(C_{x,1})\cup\cdots \cup q(C_{ x, n_x})
とできる。 O_x= p(C_{x,1})\cap\cdots\cap p(C_{x, n_x}) とすると，射影は開写像なのと，開集合の有限個の共通部分は開集合なので， O_x は開集合であり， x\in O_x かつ C_{x, 1},\ldots, C_{x, n_x} は O_x\times Y を被覆する。
すなわち，\mathcal{X} を O\times Y が \mathcal{C} に属する有限個の集合で覆えるような O\in\mathcal{O} 全体の集合と定めると， \{O_x\}_{x\in X}\subset \mathcal{X} より，\mathcal{X} は X の開被覆であるが， X はコンパクトより，有限部分被覆 \{X_k\}_{k=1}^m \subset\mathcal{X} があって， X = X_1\cup \cdots \cup X_m とできる。
であり，各 X_k\times Y は \mathcal{C} に属するの有限個の集合で被覆できるので， X\times Y も \mathcal{C} に属するの有限個の集合で被覆できる。よって， X\times Y もコンパクトである。
証明終
3. コンパクト性 ⇔ 有限交叉性
ド・モルガンの法則によって補集合に着目することで，コンパクトと同値な条件が作れます。
位相空間 (X, \mathcal{O}) がコンパクト空間であるとは，任意の \mathcal{C}\subset \mathcal{O} に対し，
\bigcup_{C\in \mathcal{C}}C=X ならば，ある有限部分集合 \mathcal{C}_0\subset \mathcal{C} が存在して， \bigcup_{C\in \mathcal{C}_0} C=X
ということができます。ここで， \mathcal{F} を閉集合族としましょう。すると，上の条件は，任意の \mathcal{D}\subset \mathcal{F} に対し，
\bigcup_{D\in \mathcal{D}}D^c=X ならば，ある有限部分集合 \mathcal{D}_0\subset \mathcal{D} が存在して， \bigcup_{D\in \mathcal{D}_0} D^c=X
と換言できます。さらに，ド・モルガンの法則を用いると，任意の \mathcal{D}\subset \mathcal{F} に対し，
\bigcap_{D\in \mathcal{D}}D=\emptyset ならば，ある有限部分集合 \mathcal{D}_0\subset \mathcal{D} が存在して， \bigcap_{D\in \mathcal{D}_0} D=\emptyset
といえます。さらに対偶を取ると，任意の \mathcal{D}\subset \mathcal{F} に対し，
任意の有限部分集合 \mathcal{D}_0\subset \mathcal{D} に対して， \bigcap_{D\in \mathcal{D}_0} D\ne \emptyset ならば， \bigcap_{D\in \mathcal{D}}D\ne \emptyset
と言い換えることができます。赤字の部分が成り立つとき， \mathcal{D} は有限交叉性 (finite intersection property) をもつといいます。これにより，以下の定理が成り立ちます。
定理3（コンパクト性 ⇔ 有限交叉性）
(X, \mathcal{O}) を位相空間とし，\mathcal{F} を閉集合族とする。このとき，以下は同値
- X はコンパクト空間
- 閉集合族 \mathcal{D}\subset \mathcal{F} が有限交叉性をもつならば， \bigcap_{D\in \mathcal{D}}D\ne \emptyset である。
2.とはすなわち，任意の有限個の共通部分が空でなければ，全体の共通部分も空でないと言っています。
4. ネット(有向点族)によるコンパクト性の特徴付け
例7.で，距離空間上の部分集合 A がコンパクトであることは，任意の点列 \{ a_n\}\subset A が， A 内の元に収束する部分列を含むこと(すなわち点列コンパクト)と同値だと述べました。
一般の位相空間では，点列ではダメですが，それを一般化したネット(有向点族)で，類似のことが言えます。
ネット(有向点族)の知識がないと読めませんが，一応証明をかいておきます。
証明
1.\implies 2.について
(x_\lambda)_{\lambda\in\Lambda}\subset X をネットとする。
F_\lambda =\overline{\{x_\mu \mid \mu\ge \lambda\}}
とおくと， \{ F_\lambda\}_{\lambda\in\Lambda} は有限交叉性をもつ。実際， \lambda_1,\ldots, \lambda_n\in \Lambda とすると， \Lambda は有向集合より， \mu\ge \lambda_1,\ldots,\mu\ge \lambda_n となる \mu \in\Lambda がとれ， x_\mu \in \bigcap_{k=1}^n F_{\lambda_k} となるからである。ゆえに，定理3より，x\in \bigcap_{\lambda\in\Lambda} F_\lambda が存在する。
よって， x の任意の近傍 N_x について， (x_\lambda)_{\lambda\in\Lambda} is frequently in N_x なので， x は (x_\lambda)_{\lambda\in\Lambda} の集積点である。よって，収束する部分ネットをもつ。
2.\implies1.について
\mathcal{C} を X の開被覆とする。
\Lambda = \{\lambda \subset \mathcal{C}\mid \lambda \text{ is finite}\}
を有限部分集合の族とすると，\Lambda は包含関係によって有向集合である。 X がコンパクトでないとすると，任意の \lambda\in \Lambda に対し，
が取れる。ネット (x_\lambda) は2.の仮定より集積点 x\in X をもつ。 \mathcal{C} は開被覆より，\bigcap_{C\in\mathcal{C}} (X\setminus C)=\emptyset であるが，これは矛盾している。
実際， C_x\in \mathcal{C} を x の近傍とすると， (x_\lambda) is frequently in C_x なので，ある \{C_x\}\le \lambda (すなわち \{C_x\}\subset \lambda )が存在して， x_\lambda \in C_x とならねばならないが， x_\lambda はその取り方から C_x には入らないので，矛盾している。
証明終
ネット(有向点族)で扱うと，一般のコンパクト性も明快です。
コンパクトに関連する概念
最後に，コンパクトに関係する概念を紹介しましょう。用語は[4]にならっています。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strong locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)部分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち，各点ごとに有限個の集合でしか覆われていない近傍をもつような)部分被覆をもつ |
関連する記事
参考
- 内田伏一「集合と位相」(裳華房 数学シリーズ, 増補新装版, 2020)
- 松坂和夫「集合・位相入門」 (岩波書店 数学入門シリーズ，新装版，2018)
- Gert K. Pedersen, Analysis Now. Springer, 1989.
- L. A. Steen, J. A. Seebach, Counterexamples in Topology, 2nd edition. Springer, 1978.
