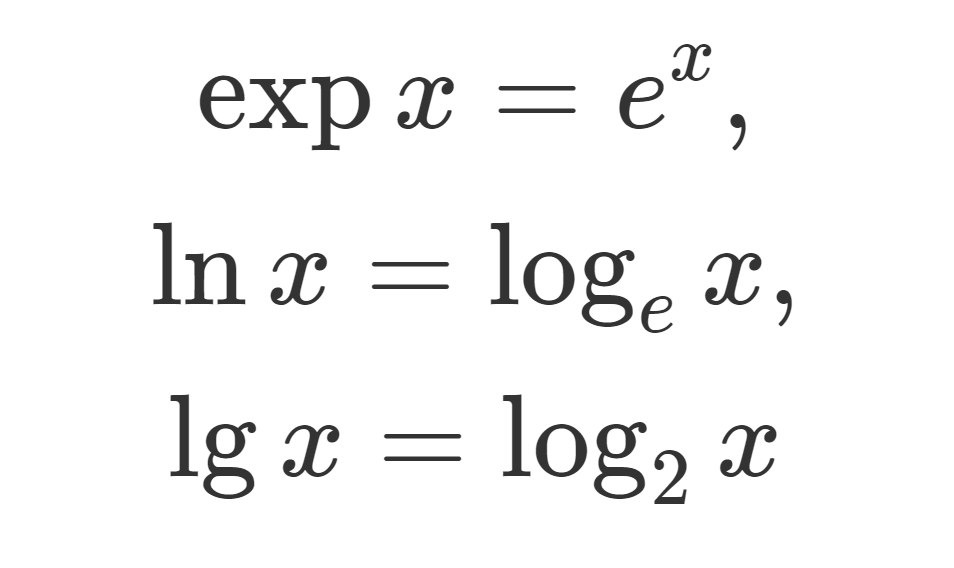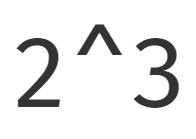数学において, \exp, \ln, \lg はそれぞれ
\begin{gathered} \exp x = e^x, \\ \ln x = \log_{e} x, \\ \lg x = \log_2 x \end{gathered}
の別表記として用いられます。これについて,詳しく掘り下げましょう。
【指数,対数の記号】数学におけるexp,ln,lg記号の意味
まずはもう一度,定義をまとめておきます。
定義( \exp, \ln, \lg 記号)
数学において, \exp, \ln,\lg はそれぞれ
\color{red} \begin{gathered} \exp x = e^x, \\ \ln x = \log_{e} x, \\ \lg x = \log_2 x \end{gathered}
の別表現である。ただし, e は自然対数の底(ネイピア数)を表す。
それぞれについて,詳しく述べましょう。
exp記号について
\exp x は e^x とかくのと同じことです。でも,指数部分が複雑だとどうでしょうか。たとえば,
\exp\left\{-t\left(\frac{\sigma^2}{2}+\int_0^\infty (1-\cos \lambda x) \, dx \right)\right\}
を,
とかくと,見づらいですよね。このような式は,たとえば,確率論における積率母関数(モーメント母関数)などで出てきます。
このようなことを避けるために,指数部分を小さく書かなくても済む \exp x という表記が使われるわけですね。
ちなみに,指数は exponential というため,その頭文字を取って \exp なわけです。
ln記号について
\ln x は,自然対数 \log_e x と同じことです。
なお,数学では,単に \log x とかいたときに, \log_e x を意味することも多いです。ただ, \log x という表現は,化学などでは常用対数 \log_{10} x にも使われますから, \log x という表現は,文脈依存です。
本サイトでは,単に \log x とかけば,それは自然対数 \log_e x を意味することにしています。数学においては,常用対数を使う場面は少ないですから,日本における多くの書籍でも,そうなっていると思います。(ただし,海外のものは \ln となっているものも一定数あると思います。)
なお, \ln の読み方については,単に「エルエヌ」とか「ログ」と読むのでよいです。由来は natural logarithm とか,ラテン語とか言われていますが,よくわかりません。
lg記号について
\lg x は,2進対数 \log_2 x の意味です。上2つに比べれば,少々マイナーかもしれません。
「計算機科学」や「情報系」において,しばしば使われることがあります。コンピューターは, 0, 1 の文字列,すなわち2進数でデータを処理するため,そういった分野においては,2進対数の都合がいい訳ですね。
ただし,ISO国際規格では,2進対数は \lg x ではなく, \operatorname{lb} x とされています。また,文脈が明らかなときは \log x とかくこともあります。一方で, \lg x は常用対数 \log_{10} x を表すこともあるので,注意が必要です。
ちなみに,2進対数は,英語で Binary logarithm といいます。