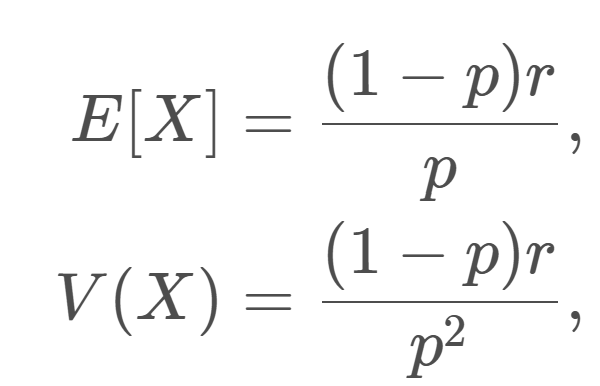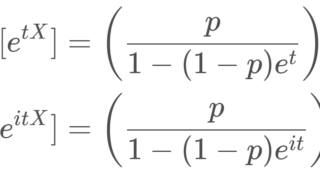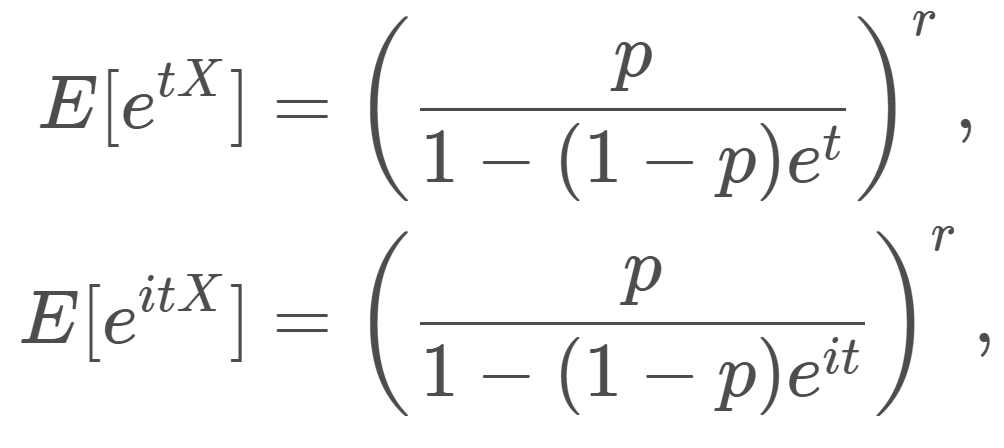PR

負の二項分布の期待値(平均)・分散・標準偏差とその導出証明

2021.07.13
確率論
大学教養
記事内に広告が含まれています。

負の二項分布 NB(r,p) について，その期待値(平均)・分散・標準偏差はそれぞれ

\begin{aligned} E[X] &= \dfrac{pr}{1-p},\\ V(X)&= \dfrac{pr}{(1-p)^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{pr}}{1-p} \end{aligned}


となります。これについて「直接証明する方法」「特性関数の微分を用いる方法」の2通りで証明しましょう。

負の二項分布の期待値(平均)・分散・標準偏差

定理（負の二項分布の期待値(平均)・分散・標準偏差）

X\sim NB(r, p) とする。このとき， X の期待値(平均)・分散・標準偏差は

\color{red} \begin{aligned} E[X] &= \dfrac{pr}{1-p},\\ V(X)&= \dfrac{pr}{(1-p)^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{pr}}{1-p} \end{aligned}


である。

証明に入る前に，負の二項分布の復習をしておきます。

負の二項分布の定義

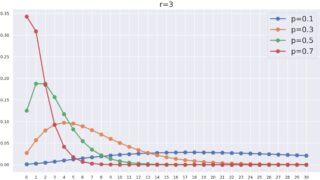
0<p<1, \, r\ge 1 を整数とする。確率変数 X が k = 0,1,2,\ldots に対し，

\color{red}\begin{aligned} P(X=k) &= {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r \\ &= {}_{k+r-1}\mathrm{C}_{r-1}\, p^k(1-p)^r \end{aligned}


となるとき， X はパラメータ (r, p) の負の二項分布 (negative binomial distribution) に従うという。本記事では，\color{red} X\sim NB(r,p) とかくことにする。

負の二項分布全般の性質については，以下でまとめています。

負の二項分布の定義と例と性質まとめ
コイン投げをしたときの失敗回数を固定し，その失敗回数に到達するまでの成功回数を数える負の二項分布NB(r, p) (negative binomial distribution) について，その定義と例と性質をまとめましょう。
mathlandscape.com

負の二項分布の期待値(平均)の導出証明

さて，早速進めていきます。

  • 定義から直接証明する方法
  • 特性関数の微分を用いる方法

の2通りで証明しましょう。

【期待値】定義から直接証明する方法

証明

期待値の定義より，

\begin{aligned} E[X]&= \sum_{k=0}^\infty k P(X=k) \\ &= \sum_{k=0}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r \\ &= \sum_{k=1}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r. \end{aligned}


ここで， k\ge 1 のとき

\begin{aligned}k \,{}_{k+r-1}\mathrm{C}_{k} &= k\cdot \frac{(k+r-1)!}{k!(r-1)!} \\ &= r \cdot \frac{(k+r-1)!}{(k-1)!r!} \\ &= r \, {}_{k+r-1}\mathrm{C}_{k-1} \end{aligned}


であるから，

\begin{aligned} E[X] &= r \sum_{k=1}^\infty {}_{k+r-1}\mathrm{C}_{k-1}\, p^k (1-p)^r \\ &= r \sum_{k=0}^\infty {}_{k+r}\mathrm{C}_{k}\, p^{k+1} (1-p)^r \\ &= \frac{pr}{1-p} \sum_{k=0}^\infty {}_{k+r}\mathrm{C}_{k} \,p^k (1-p)^{r+1} \\ &= \frac{pr}{1-p} \sum_{k=0}^\infty P(Y=k) \\ &= \frac{pr}{1-p} \end{aligned}


である。ただし， Y\sim NB(r+1, p) と定めた。以上から， E[X] = \dfrac{pr}{1-p} .

証明終

【期待値】特性関数の微分を用いた方法

特性関数の微分を用いる方法を証明する前に，負の二項分布の特性関数を確認しておきます。

負の二項分布の特性関数
\color{red} E[e^{itX}]=\left(\dfrac{1-p}{1-pe^{it}}\right)^r,\quad t\in\mathbb{R}
負の二項分布の積率母関数(モーメント母関数)・特性関数とその導出
負の二項分布NB(r, p)における，積率母関数(モーメント母関数)・特性関数をそれぞれ提示し，それの導出ついての証明をおこないましょう。
mathlandscape.com

証明

特性関数の両辺を t で微分すると，

E[iXe^{itX}] = \frac{ipre^{it}}{1-pe^{it}} \left(\dfrac{1-p}{1-pe^{it}}\right)^{r}

両辺 t=0 を代入すると，

E[iX] = \frac{ipr}{1-p}


であるから， E[X] = \dfrac{pr}{1-p} .

証明終

なお，今回は特性関数を用いましたが，積率母関数(モーメント母関数)を用いても，同様に証明できます。

負の二項分布の分散の導出証明

さて，分散の証明も，

  • 定義から直接証明する方法
  • 特性関数の微分を用いる方法

の2通りで証明しましょう。 V(X) = E[X^2] - E[X]^2 を用います。

【分散】定義から直接証明する方法

証明

まず，期待値の2次モーメントについて，

\begin{aligned} &E[X^2] \\ &= \sum_{k=0}^\infty k^2 P(X=k) \\ &= \sum_{k=0}^\infty k^2 \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r \\ &\quad + \sum_{k=1}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r + E[X] \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r + \dfrac{pr}{1-p} \end{aligned}


である。ここで， k\ge 2 のとき，

\begin{aligned} &k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\\ &= k(k-1)\cdot \frac{(k+r-1)!}{k!(r-1)!} \\ &= (r+1)r\cdot \frac{(k+r-1)!}{(k-2)!(r+1)!} \\ &= (r+1)r\, {}_{k+r-1}\mathrm{C}_{k-2}\end{aligned}


であるから，

\begin{aligned} &\sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^k(1-p)^r \\ &= (r+1)r \sum_{k=2}^\infty \,{}_{k+r-1}\mathrm{C}_{k-2}\, p^k(1-p)^r\\ &= (r+1)r \sum_{k=0}^\infty \,{}_{k+r+1}\mathrm{C}_{k}\, p^{k+2}(1-p)^r\\ &= \frac{p^2(r+1)r}{(1-p)^2} \sum_{k=0}^\infty \,{}_{k+r+1}\mathrm{C}_{k}\, p^{k}(1-p)^{r+2}\\ &= \frac{p^2(r+1)r}{(1-p)^2} \sum_{k=0}^\infty P(Z=k) \\ &= \frac{p^2(r+1)r}{(1-p)^2} \end{aligned}


ただし， Z\sim NB(r+2 ,p) とした。よって，

E[X^2] =\frac{p^2(r+1)r}{(1-p)^2} + \frac{pr}{1-p}


なので，

\begin{aligned}V(X) &= E[X^2]-E[X]^2 \\ &=\frac{p^2(r+1)r}{(1-p)^2} + \frac{pr}{1-p} - \left(\frac{pr}{1-p}\right)^2 \\ &= \frac{pr}{(1-p)^2}. \end{aligned}

証明終

【分散】特性関数の微分を用いる方法

証明

特性関数の式 E[e^{itX}]=\left(\dfrac{1-p}{1-pe^{it}}\right)^r,\quad t\in\mathbb{R} の両辺 t で2回微分すると，

E[(iX)^2e^{itX}] = - \frac{pre^{it}(1+pre^{it})}{(1-pe^{it})^2} \left(\dfrac{1-p}{1-pe^{it}}\right)^r


となる。両辺 t=0 を代入して -1 倍すると，

E[X^2] = \frac{pr(1+pr)}{(1-p)^2}.


したがって，

\begin{aligned} V(X) &= E[X^2] - E[X]^2 \\ &= \frac{pr(1+pr)}{(1-p)^2} - \left(\dfrac{pr}{1-p}\right)^2 \\ &= \frac{pr}{(1-p)^2}.\end{aligned}

証明終

負の二項分布の標準偏差について

標準偏差は，分散の平方根 \sqrt{V(X)} でしたから，上で分散を求めたことで，

\sqrt{V(X)} = \frac{\sqrt{pr}}{1-p}


と求まりますね。

負の二項分布に関する記事

負の二項分布の定義と例と性質まとめ
コイン投げをしたときの失敗回数を固定し，その失敗回数に到達するまでの成功回数を数える負の二項分布NB(r, p) (negative binomial distribution) について，その定義と例と性質をまとめましょう。
mathlandscape.com