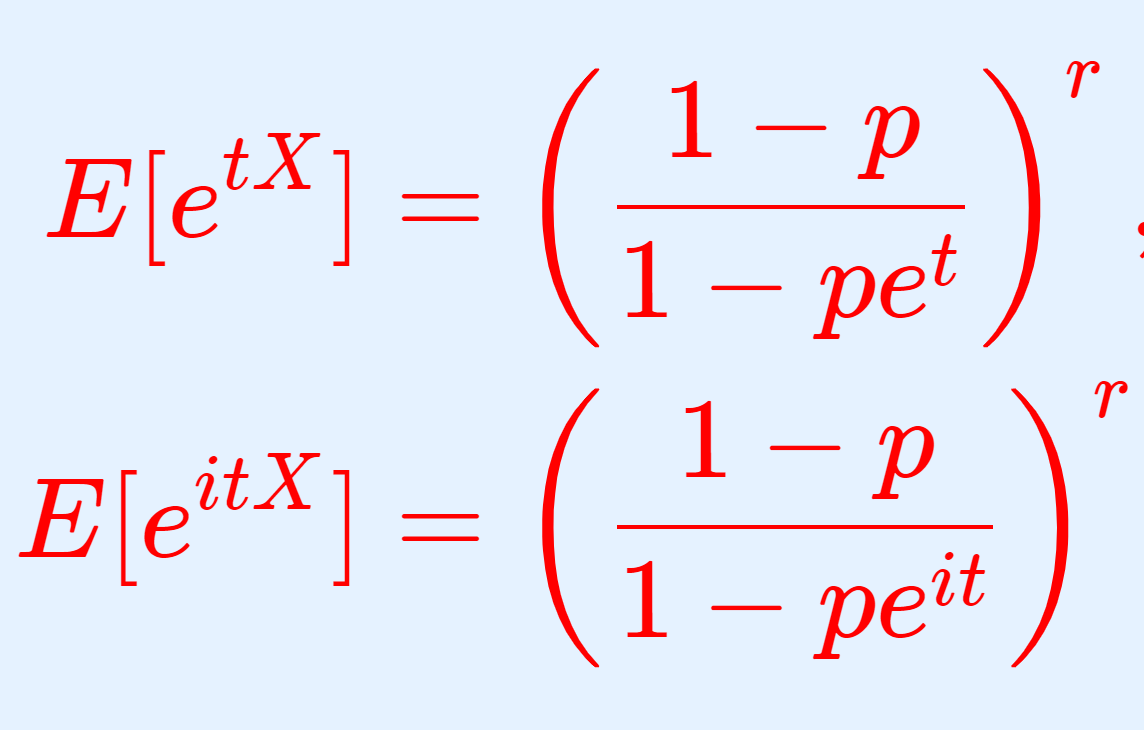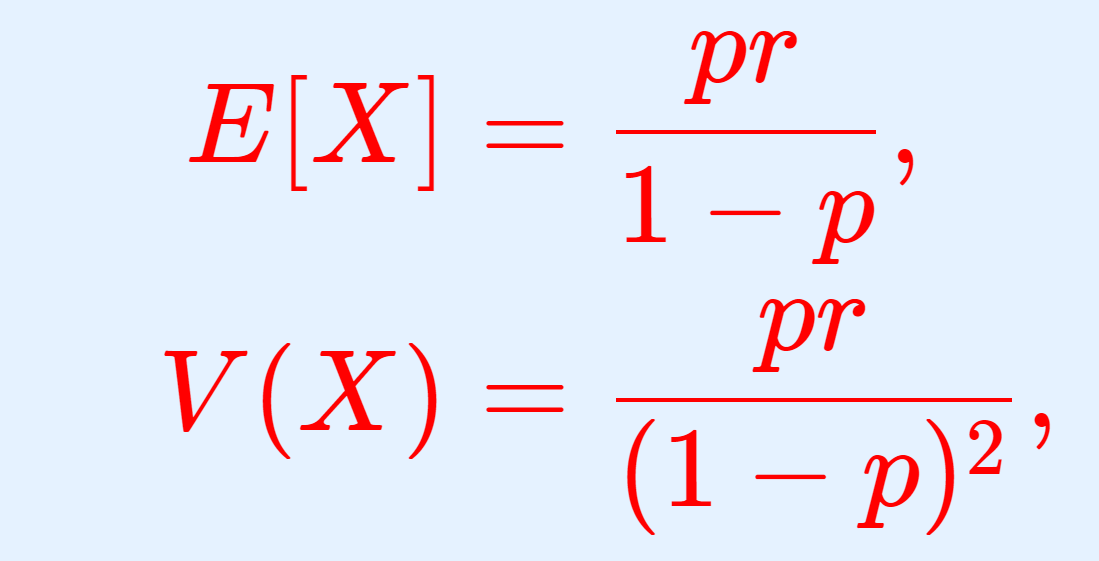負の二項分布の積率母関数(モーメント母関数)・特性関数とその導出

負の二項分布 $NB(r, p)$ における，積率母関数(モーメント母関数)・特性関数はそれぞれ

\begin{aligned} E[e^{tX}] &= \left(\dfrac{1-p}{1-pe^t}\right)^r,\quad t<-\log p,\\ E[e^{itX}]&=\left(\dfrac{1-p}{1-pe^{it}}\right)^r,\quad t\in\mathbb{R} \end{aligned}

となります。これについて，その導出の証明を行いましょう。

負の二項分布の積率母関数(モーメント母関数)・特性関数

定理（負の二項分布の積率母関数(モーメント母関数)・特性関数）

$X\sim NB(r, p)$ とする。このとき， $X$ の積率母関数(モーメント母関数)・特性関数は

\color{red} \begin{aligned} E[e^{tX}] &= \left(\dfrac{1-p}{1-pe^t}\right)^r,\quad t<-\log p,\\ E[e^{itX}]&=\left(\dfrac{1-p}{1-pe^{it}}\right)^r,\quad t\in\mathbb{R} \end{aligned}

である。

後半については，複素数の累乗を考えていますが，正の整数乗なので，あまり深刻ではありません。単に複素数を $r$ 回掛けるだけです。

証明に入る前に，負の二項分布の定義を復習しておきましょう。

負の二項分布の定義

$0<p<1, \, r\ge 1$ を整数とする。確率変数 $X$ が $k = 0,1,2,\ldots$ に対し，

\color{red}\begin{aligned} P(X=k) &= {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r \\ &= {}_{k+r-1}\mathrm{C}_{r-1}\, p^k(1-p)^r \end{aligned}

となるとき， $X$ はパラメータ $(r, p)$ の負の二項分布 (negative binomial distribution) に従うという。本記事では， $\color{red} X\sim NB(r,p)$ とかくことにする。

負の二項分布の定義と性質まとめについては，以下で解説しています。

まず，二項分布の積率母関数(モーメント母関数)の導出から始めましょう。

証明

期待値と負の二項分布の定義から，

\begin{aligned} E[e^{tX}] &= \sum_{k=0}^\infty e^{tk} P(X=k) \\ &= \sum_{k=0}^\infty e^{tk} {}_{k+r-1}\mathrm{C}_k\, p^k(1-p)^r \\ &=(1-p)^r \sum_{k=0}^\infty {}_{k+r-1}\mathrm{C}_k\, (pe^t)^k \end{aligned}

であり，この無限和が収束するには， $pe^t < 1$ すなわち， $t<-\log p$ が必要である。このとき，

\begin{aligned} &(1-p)^r \sum_{k=0}^\infty {}_{k+r-1}\mathrm{C}_k\, (pe^t)^k \\ &= \left(\frac{1-p}{1-pe^t}\right)^r \sum_{k=0}^\infty {}_{k+r-1}\mathrm{C}_k\, (pe^t)^k (1-pe^t)^r \\ &= \left(\frac{1-p}{1-pe^t}\right)^r \sum_{k=0}^\infty P(Y=k) \\ &= \left(\frac{1-p}{1-pe^t}\right)^r \end{aligned}

ただし， $Y\sim NB(r, pe^t)$ である。よって，

E[e^{tX}] = \left(\dfrac{1-p}{1-pe^t}\right)^r,\quad t<-\log p.

証明終

特性関数の方も，積率母関数(モーメント母関数)と同様の議論を，といいたいところですが，複素数の範囲で $NB(r, pe^{it})$ とするのは無理があるため，できません。今回は，積率母関数を拡張して証明しましょう。

証明

積率母関数(モーメント母関数)の等式

E[e^{tX}] = \left(\dfrac{1-p}{1-pe^t}\right)^r,\quad t<-\log p.

を $\{ z \in\mathbb{C}\mid \operatorname{Re} z < -\log p \}$ 上に解析接続することで，この上の $z$ で

E[e^{zX}] = \left(\dfrac{1-p}{1-pe^z}\right)^r

となる。 $z=it, \; t\in\mathbb{R}$ とすると，

E[e^{itX}] = \left(\dfrac{1-p}{1-pe^{it}}\right)^r

がわかる。

証明終

解析接続の議論は，複素関数論の範囲です。具体的に示すには，左辺が解析的であり，右辺も解析的であることをそれぞれ示し，よってお互い解析接続したものが等しくなる，とします。