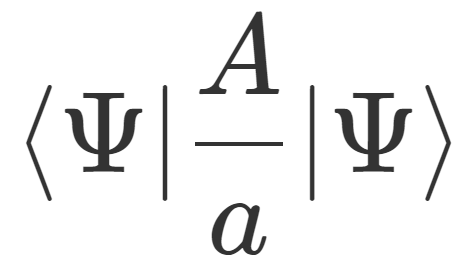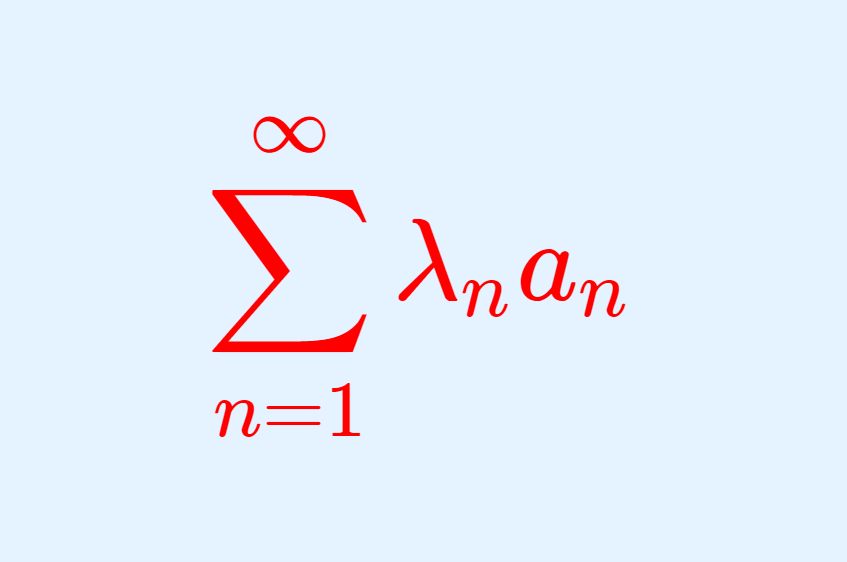集合族,または集合系とは「集合の集まり」という意味です。たくさんの集合は,添え字を用いて A_1, A_2 のように区別されます。
集合族と添字集合について,その定義と使い方を解説します。
集合族と添字集合
定義(集合族)
集合の集まりを集合族 (family of sets) または集合系という。
集合の集まりとは,「集合の集合」です。各要素が集合であるような集合を「集合族」というのですね。
たとえば,集合 A_1=\{a\}, \;A_2=\{a,b\},\; A_3=\{a,b,c\} に対して,この集まり \{A_1, A_2, A_3\} は集合族です。
このとき,各集合 A_1,A_2,A_3 の右下に添えられている 1,2,3 を添え字 (index) といい,これらを集めた集合 \{1,2,3\} を添字集合 (index set) といいます。
さらにこのとき,集合族 \{A_1, A_2,A_3\} を添字集合 \{1,2,3\} で添え字付けられた集合族といいます。 定義を整理しておきましょう。
定義(添字集合)
集合族 \{A_\lambda\}_{\lambda\in\Lambda} について,その添え字の集合 \Lambda を添字集合 (index set) という。
また,このときの \{A_\lambda\}_{\lambda\in\Lambda} を \Lambda で添え字付けられた集合族という。
\lambda, \Lambda はそれぞれ小文字・大文字のラムダです。
集合族を \{A_\lambda\}_{\lambda\in\Lambda} のように書きましたが,このような,「集合族のかき方」については,今から掘り下げることにしましょう。
集合族のかき方
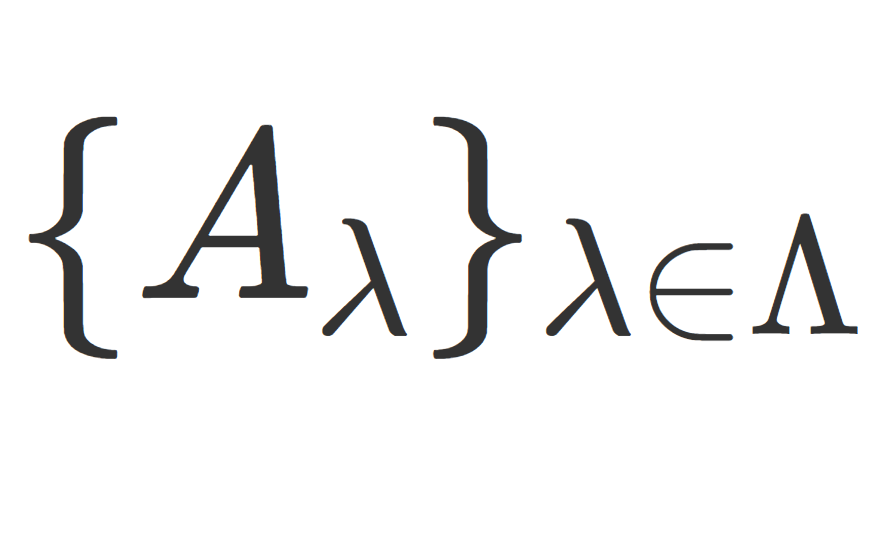
ここからは,集合族のかき方について見ていきましょう。
有限個の集合族
有限個の集合族は, 1,2,3,\dots, n のように,正の整数で番号をつけることが多いです。これを用いて,集合族は \color{red} \{A_k\}_{k=1}^n のように書くことが多いです。このとき,添字集合は \{1,2,3,\dots, n\} です。
あるいは, 0 から始めて \color{red} \{A_k\}_{k=0}^{n-1} などとすることもあります。このとき,添字集合は \{0,1,2,\dots, n-1\} です。
数字を振れば,集合が n 個集まっていることが容易にわかりますね。
可算個の集合族
続いて,可算個の集合族を考えましょう。「可算個」とは,簡単に言うと 1,2,3,\dots のように,正の整数で番号付けできることを指します(→可算集合と非可算集合(可算無限・非可算無限))。
整数で番号付けできるわけですから,可算個の集合族は \color{red} \{A_n\}_{n=1}^\infty のように書きます。あるいは,0 から始めて \color{red} \{A_n\}_{n=0}^\infty とかくこともあるでしょう。このとき,添字集合はそれぞれ \mathbb{Z}_{\ge 1}, \mathbb{Z}_{\ge 0} です。
番号が明らかなときは,単に \color{red}\{A_n\} とかくこともあります。
可算個は正の整数で番号付けできていますから, A_1, A_2, A_3, のように,一列に並べることができます。このため,この集合族を集合列 (sequence of sets) ということがあります。「数列」は数ですが,それの集合バージョンって感じですね。
一般の集合族
一般の集合族,特に非可算個も含めた集合族は,整数による番号付けは不可能です(→可算集合と非可算集合(可算無限・非可算無限))。
よって,一般の集合 \Lambda を用いて, \color{red} \{A_\lambda\}_{\lambda\in \Lambda} などのように添え字付けします。このとき,添字集合は \Lambda (ラムダ)です。
添字集合 \Lambda が明らかなときは,単に \color{red} \{A_\lambda \} とかくこともあります。