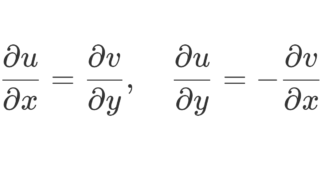複素関数の微分～定義と例～

複素数の関数における微分は，実数のときと同じく，

f'(z)=\lim_{h\to 0} \frac{f(z+h)-f(z)}{h}

の形で定義されます。これについて，具体例を交えて詳しく解説します。

複素関数の微分の定義

以下， $\mathbb{C}$ は複素数全体の集合としましょう。

定義（複素関数の微分）

$f\colon \mathbb{C}\to\mathbb{C}$ が $z\in\mathbb{C}$ で微分可能 (differentiable) であるとは，

\color{red} f'(z)=\lim_{h\to 0} \frac{f(z+h)-f(z)}{h}

が存在することをいう。

形は実数関数のときの微分と全く同じですね。

微分の定義において， $h\to 0$ は $h\in\mathbb{C}$ の範囲で極限を取っていることに注意してください。 $z+h$ は，下図のように，うろうろしながら近づけても構いません。

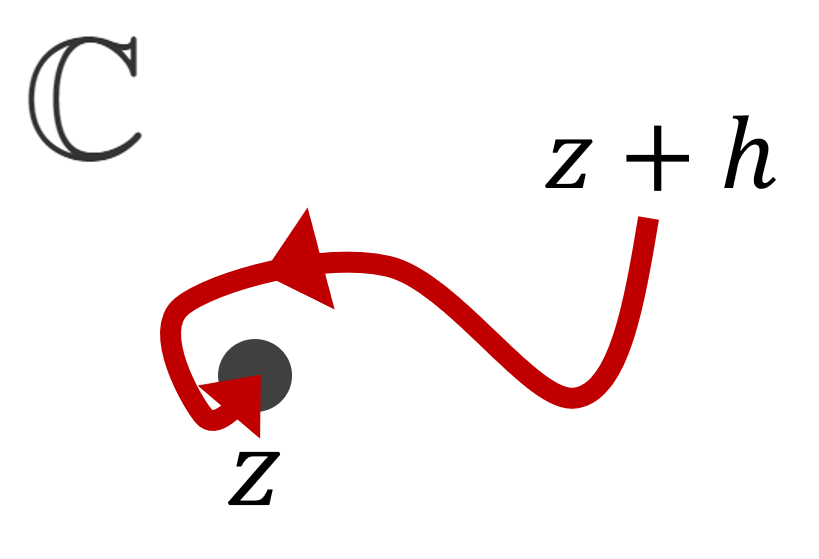
複素数の微分は，実数とほぼ同様に計算できます。具体例を見ていきましょう。

例1.

$n\ge 1$ を整数とする。 $\color{red} f(z)=z^n$ は

\begin{aligned}f'(z)&=\lim_{h\to 0} \frac{(z+h)^n-z^n}{h} \\ &= \lim_{h\to 0}\sum_{k=1}^{n} {}_n \mathrm{C}_k z^{n-k} h^{k-1 }\\ &= nz^{n-1} \end{aligned}

なので， $\color{red}f'(z)=nz^{n-1}$ である。

計算過程を見ると，極限の計算は，実数のときと全く同じと思ったのはないでしょうか。このように，複素微分でも，実数のときと同じように考えればよい場合が多いです。実際，次の例が成立します。

例2.

実数のときと類似の計算により，

実数のときとほぼ同じですね。続いて，微分不可能な場合も見ていきましょう。

例3.

$\color{red} f(z)=\overline{z}$ (共役複素数) とする。これは，任意の点で微分不可能である。実際，

\frac{f(z+h)-f(z)}{h}=\frac{\overline{h}}{h}

となって， $h=a\in\mathbb{R}$ とすると $1$ ， $h=ia$ とすると $-1$ になってしまい，極限が一意に定まらないからである。

微分不可能な例です。このように， $f$ の定義に $\overline{z}$ が入っていると，基本的に微分できないと思ってよいです。

例4.

$f(z)=|z|^2$ とする。これは， $z\ne 0$ で微分不可能である。実際，

\frac{|z+h|^2 - |z|^2}{h} = \overline{z}+ \overline{h}+z\frac{\overline{h}}{h}

なので， $z\ne 0$ のときは $h\to 0$ の極限は一意に定まらないからである。

これも， $f(z)=|z|^2 = z\overline{z}$ であり， $f$ の定義に $\overline{z}$ が入っていて，原点以外では微分できません。

複素数は $z= x+iy \; (x,y\in\mathbb{R})$ と解釈することで，

f(z)=u(x,y)+iv(x,y)

のような実2変数関数 $u,v$ と思うことができます。では，複素微分可能であるためには，実2変数関数としてどのような条件が必要でしょうか。これは，コーシーリーマンの関係式として知られています。以下の記事で解説しています。

$D\subset \mathbb{C}$ を開領域とし，この上で定義された複素関数 $f\colon D\to \mathbb{C}$ について， $D$ 全体で微分可能であるとき， $f$ を正則関数 (regular function) といいます。

正則関数は，以下のような強力な定理が成立します。

定理（正則関数は解析的）

$f\colon D\to \mathbb{C}$ を正則とするとき，これは各点の周りで解析的である。特に，無限回微分可能（ $C^\infty$ 級）である。

「解析的」とは，近傍でテイラー展開可能であることを指します(→テイラー展開・マクローリン展開とは【解析的な関数と具体例】)。

1回微分可能を課しただけなのに，無限回微分可能で，しかもテイラー展開可能であることまで言えてしまうのはすごいですね。複素関数が微分可能であるというのは，非常に良い性質を指しているわけです。

このことについて，詳しくは，またいつかの機会に解説しましょう。