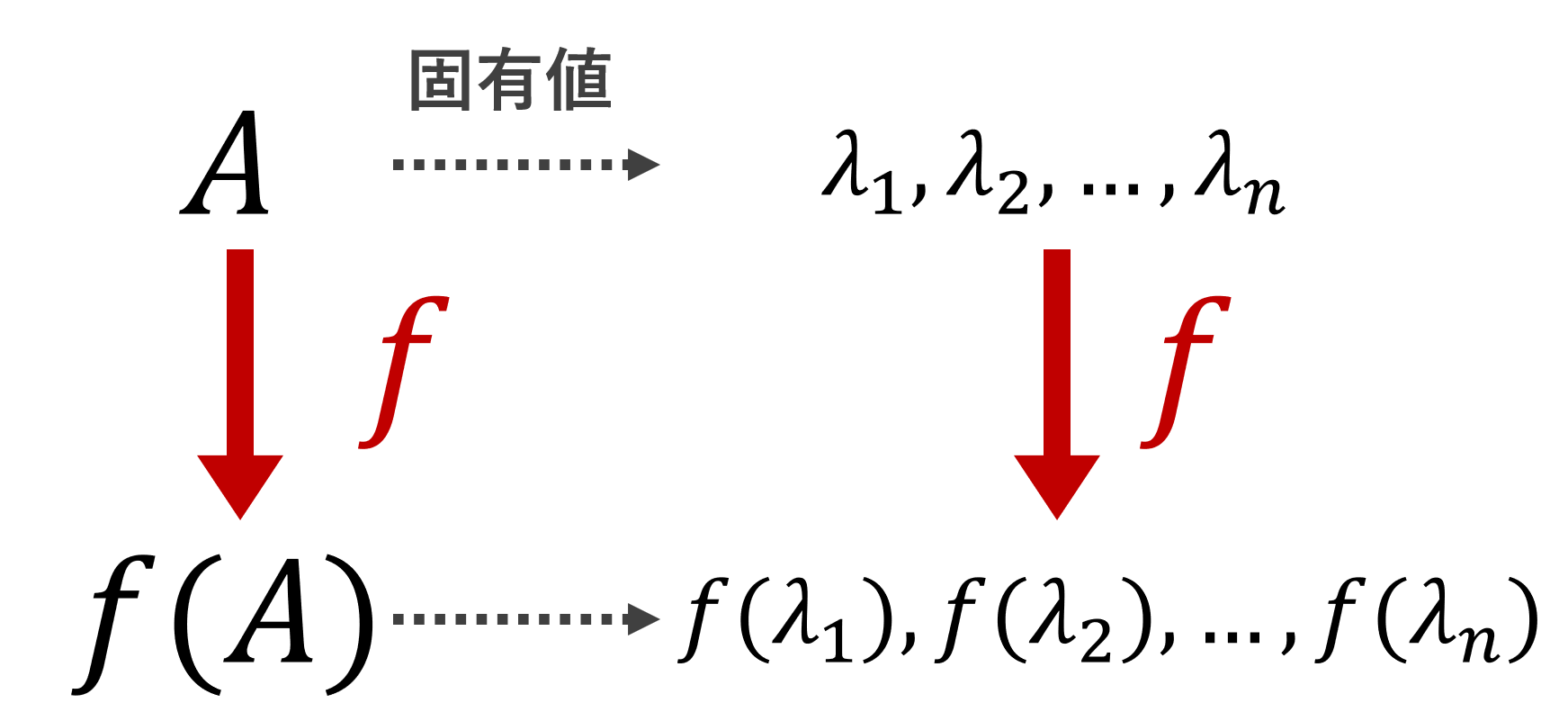
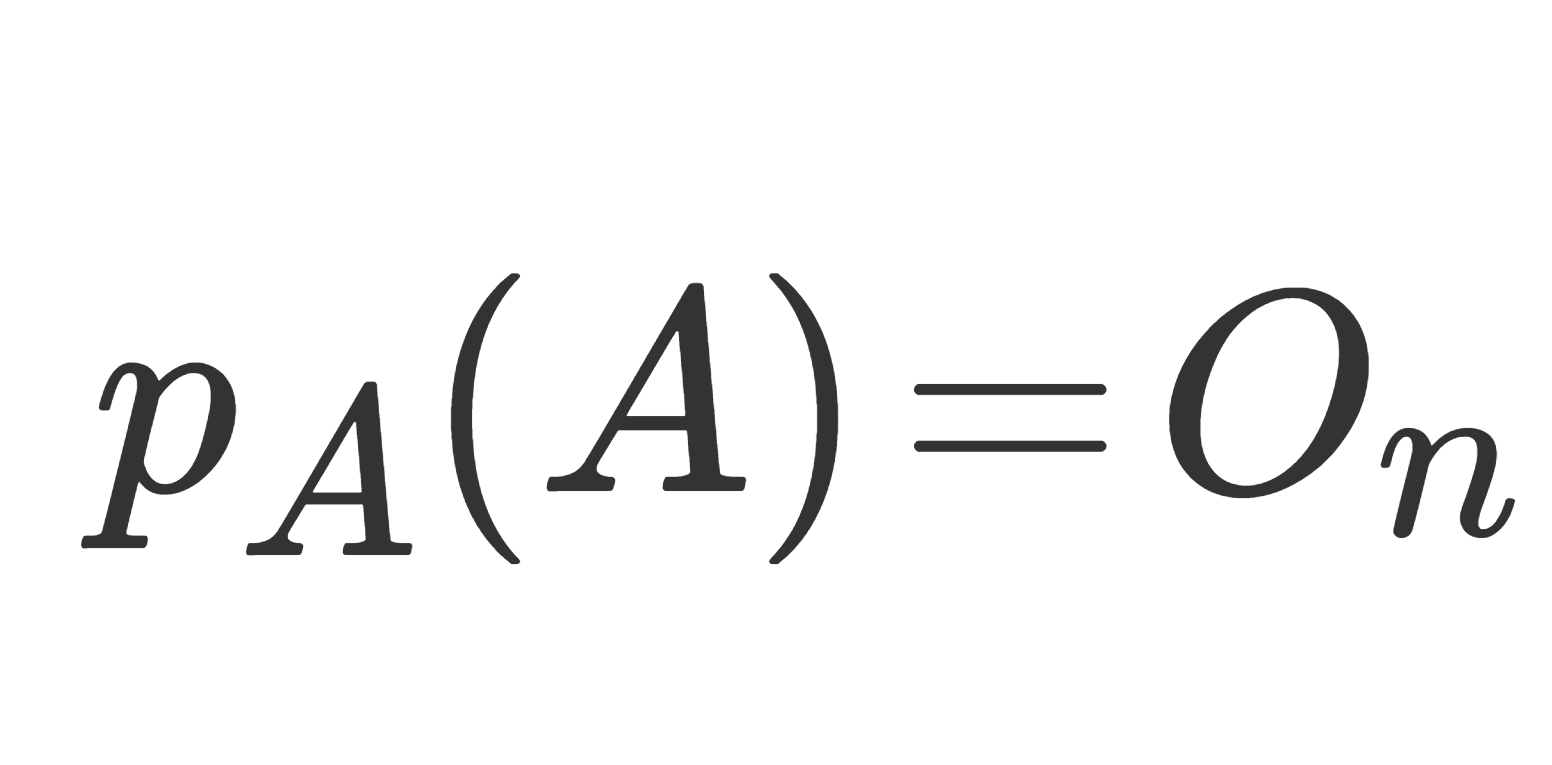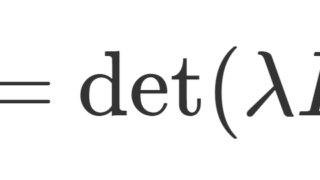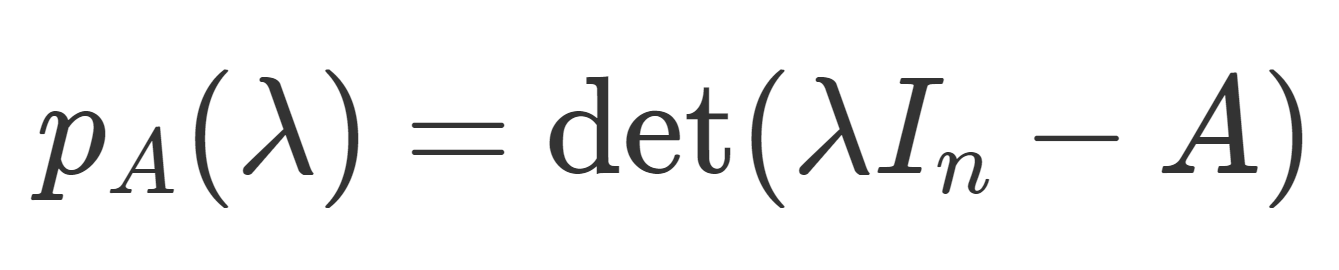PR

ケーリーハミルトンの定理とその厳密な証明をわかりやすく

線形代数学

2021.11.242021.11.25

線形代数学

記事内に広告が含まれています。

ケーリーハミルトンの定理とは，正方行列 $A$ の固有多項式 $p_A(\lambda)$ に対し， $p_A(A)=O_n$ となる定理です。

$A$ が零行列になるような最小多項式 $f(\lambda)$ は $p(\lambda)$ を割り切ることが知られています（今回はこれについて紹介しません。これについては行列の固有多項式・最小多項式の定義・求め方・性質を参照してください）。今回は，最小多項式の基にもなっているケーリーハミルトンの定理について紹介します。

目次

ケーリーハミルトンの定理
1. 2次のときの例
2. よくある勘違い
ケーリーハミルトンの定理の厳密な証明
関連する記事

ケーリーハミルトンの定理

ケーリーハミルトンの定理

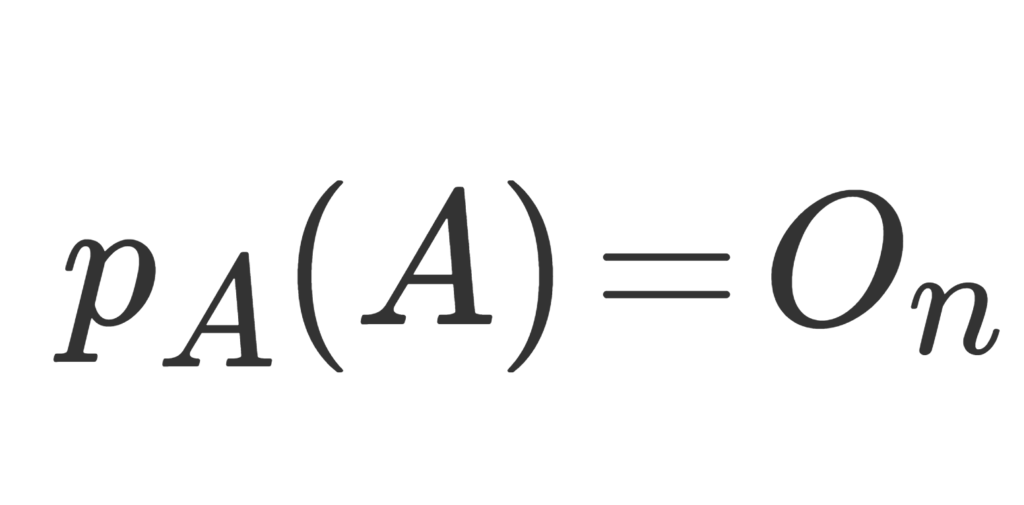
ケーリーハミルトンの定理 (Cayley-Hamilton theorem)

$A$ を $n$ 次正方行列とし， $p_A (\lambda)=\det (\lambda I_n -A)$ をその固有多項式とする。このとき，固有多項式 $p_A(\lambda)$ の変数 $\lambda$ に行列 $A$ を当てはめた $p_A(A)$ について

\large \color{red} p_A(A)=O_n

が成立する。 $I_n,O_n$ は $n$ 次単位行列・零行列ある。

「ケーリー」さんと「ハミルトン」さんの定理です。ケーリー・ハミルトンの定理，ハミルトン・ケーリーの定理ともいいます。

2次のときの例

一般の場合の証明をする前に，2次のときの例を確認しましょう。

2次のときの例

$A=\begin{pmatrix} a& b\\ c& d\end{pmatrix}$ の固有多項式は

\begin{aligned}p_A(\lambda)&=\det (\lambda I_2-A)=\begin{vmatrix} \lambda-a & -b \\ -c & \lambda -d \end{vmatrix}\\ &=(\lambda-a)(\lambda-d)-(-b)(-c)\\ &=\lambda^2-(a+d)\lambda +ad-bc \end{aligned}

である。この固有多項式に $A$ を代入すると，

\begin{aligned}p_A(A)&= A^2-(a+d)A+(ad-bc)I_2 \\ &= \begin{pmatrix}a^2+bc& b(a+d)\\ c(a+d)& bc+d^2 \end{pmatrix}\\&-(a+d) \begin{pmatrix} a& b\\ c& d\end{pmatrix} +(ad-bc) \begin{pmatrix} 1& 0\\ 0& 1\end{pmatrix}\\ &= \begin{pmatrix} 0& 0\\ 0& 0\end{pmatrix} \end{aligned}

となり，確かにケーリーハミルトンの定理が成立する。

よくある勘違い

実際の証明に入る前に，よくある勘違いについて紹介しておきましょう。

間違った証明

$p_A(\lambda)=\det (\lambda I_n-A)$ より，

p_A(A)= \det (AI_n -A) = \det O_n = 0.

これは「 $\lambda$ に $A$ を代入する」の意味を勘違いしています。そもそも示すべきは $p_A(A)=O_n$ であって $p_A(A)=0$ ではありません。

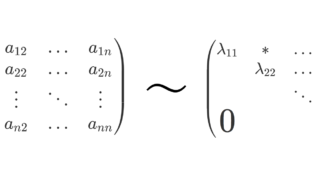
p_A(\lambda)= \begin{vmatrix} \lambda-a_{11} & -a_{12} &\dots & -a_{1n} \\ -a_{21} & \lambda -a_{22}& \dots& -a_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ -a_{n1} & -a_{n2} & \dots & \lambda - a_{nn}\end{vmatrix}

であり，右辺に $\lambda = A$ を代入するというのは意味の分からない話ですね。このように，どの段階で $\lambda =A$ を代入するかで解釈が変わります。今回は， $p_A(\lambda)$ を多項式と見た後に行列を代入すると言っているわけですね。注意しましょう。

ケーリーハミルトンの定理の厳密な証明

さて，ケーリーハミルトンの定理を厳密に証明していきましょう。任意の正方行列は，上三角行列と相似であることを用います。

証明

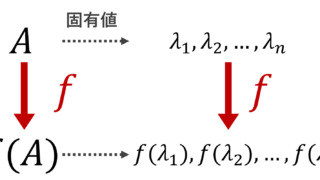
正方行列 $A$ に対し，正則行列(可逆行列) $P$ が存在して， $T=P^{-1}AP$ が上三角行列としてよい。このとき， $A$ と $T$ の固有値は同じであり， $T$ の対角成分に固有値が並ぶ(→行列の相似とは～定義と性質6つの証明～・上三角行列・下三角行列の定義と性質6つ)。そこで，

\begin{aligned}p_A(\lambda)&=p_T(\lambda)=(\lambda-\lambda_1)\dots (\lambda-\lambda_n),\\ T&= \begin{pmatrix} \lambda_{1}& * & \dots & * \\ & \lambda_{2} &\dots & * \\ &&\ddots & \vdots \\ \huge{0}&&&\lambda_{n} \end{pmatrix} \end{aligned}

とかくことにする。 $\boldsymbol{x}=\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_{n-1}\\x_n \end{pmatrix} \in\mathbb{C}^n$ とすると，

\begin{aligned} &p_T(T)\boldsymbol{x}\\&=(T-\lambda_1I_n)\dots (T-\lambda_nI_n) \boldsymbol{x} \\ &= (T-\lambda_1I_n)\dots\begin{pmatrix} *& * & \dots & * \\ & * &\dots & * \\ &&\ddots & \vdots \\ \huge{0}&&&0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_{n-1}\\x_n \end{pmatrix} \\ &= (T-\lambda_1I_n) \dots (T-\lambda_{n-1}I_n) \begin{pmatrix} * \\ * \\ \vdots \\ *\\ 0 \end{pmatrix}\\ &= (T-\lambda_1I_n) \dots (T-\lambda_{n-2}I_n) \begin{pmatrix} * \\ * \\ \vdots \\ 0\\0 \end{pmatrix} \\ &=\dots = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0\\0 \end{pmatrix} \end{aligned}

であるから， $p_T(T)=O_n$ である。ここで

\begin{aligned}p_T(T) &=p_T(P^{-1}AP)\\&= ( P^{-1}AP -\lambda_1I_n)\dots ( P^{-1}AP -\lambda_nI_n)\\ &= P^{-1} (A-\lambda_1 I_n)P \dots P^{-1}(A-\lambda_nI_n)P\\ &= P^{-1} (A-\lambda_1 I_n) \dots (A-\lambda_nI_n)P\\ &= P^{-1} p_A(A) P\\ \end{aligned}

であるから， $p_A(A)=O_n$ である。

証明終

三角行列という扱いやすい行列にしてから考えてあげることで，きれいに証明できましたね。

関連する記事