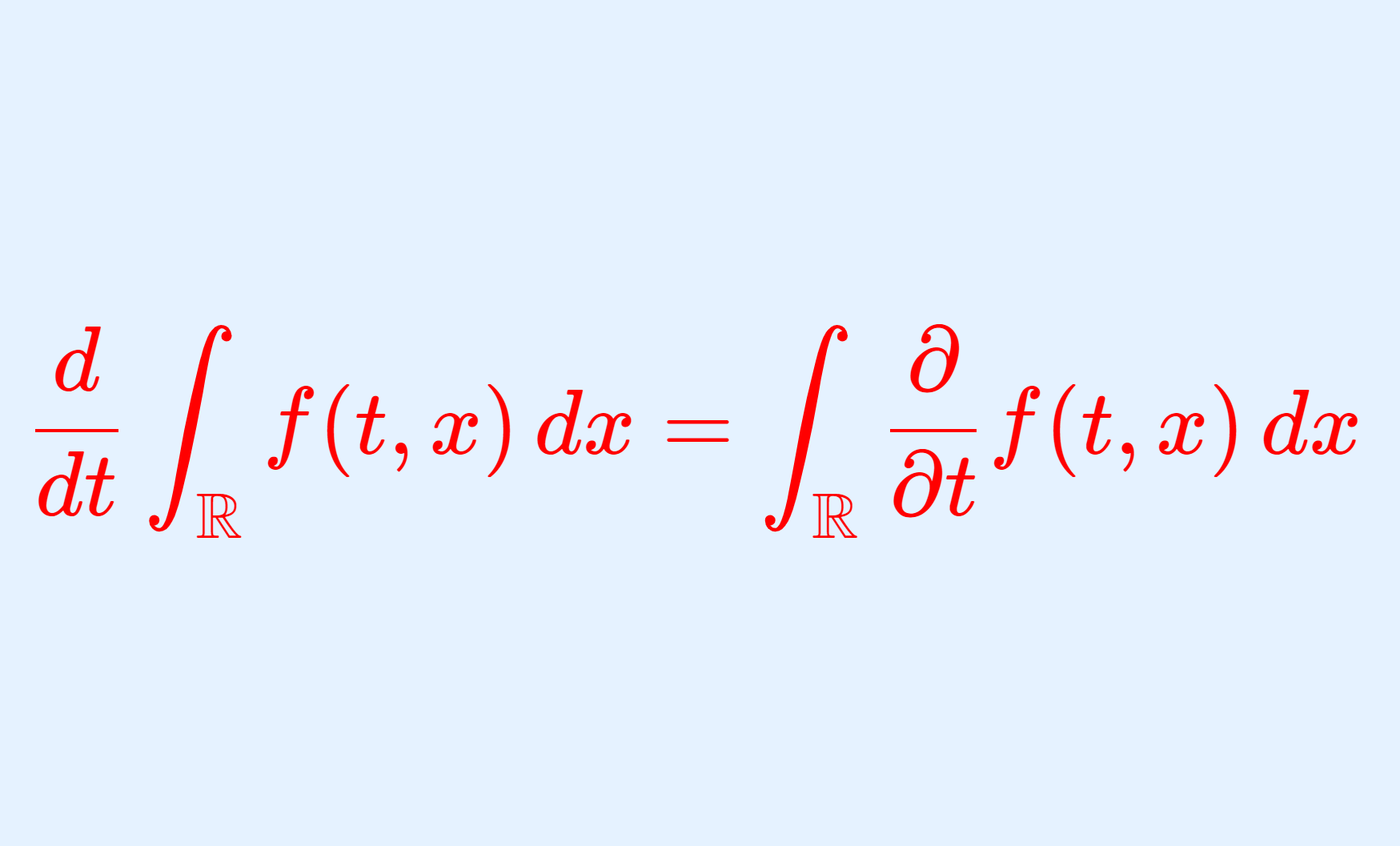PR

微分と積分の交換定理とその証明・具体例2つ

測度論

2022.02.052022.02.12

記事内に広告が含まれています。

ルベーグの収束定理(優収束定理)をもととした，微分と積分の交換定理について，その主張と証明・さらに具体例を挙げましょう。

目次

微分と積分の交換定理
微分と積分の交換の具体例
関連する記事

微分と積分の交換定理

$f \colon\mathbb{R}\to\mathbb{R}$ が可積分 (integrable) とは， $\int_\mathbb{R} |f|\,dx<\infty$ が成り立つことを指します。

定理（微分と積分の交換）

$I\subset \mathbb{R}$ を開区間とし， $f\colon I\times\mathbb{R} \to \mathbb{R}$ は以下をみたすとする。

各 $t\in I$ ごとに $f(t,\cdot)$ は可積分である。
各 $x\in\mathbb{R}$ ごとに $\frac{\partial}{\partial t}f(\cdot, x)$ が存在する。
任意の $t_0\in I$ に対して，ある $\delta>0$ と可積分関数 $G$ が存在して，
$\sup_{|t-t_0|\le \delta}\left| \frac{\partial}{\partial t} f(t,x)\right|\le G(x)$
となる。

このとき，

\color{red}\frac{d}{dt}\int_\mathbb{R} f(t,x)\,dx =\int_\mathbb{R} \frac{\partial}{\partial t} f(t,x)\,dx

が成り立つ。

$\delta$ や $G$ の取り方は，当然 $t_0\in I$ の取り方に依存して構いません。

この定理は覚えなくても，ルベーグの収束定理(優収束定理)から簡単に導けるものですから，個人的にはそのことさえ知っておけばよいと思います。実際に証明を見ておきましょう。

証明

$F(t) = \int_{\mathbb{R}} f(t,x)\,dx$ とおく。 $t_0\in\mathbb{R}$ を一つ固定する。このとき，仮定をみたす $\delta, G$ が取れる。 $0< |h|<\delta$ に対し，

\!\!\!\frac{F(t+h)-F(t)}{h} = \!\int_\mathbb{R} \!\frac{f(t+h,x)-f(t,x)}{h}\,dx.

平均値の定理より，ある $0<\theta_{t,h,x}<1$ が存在して，

\begin{aligned}\left|\frac{f(t+h,x)-f(t,x)}{h}\right|&=\left|\frac{\partial}{\partial t}f(t+\theta_{t,h,x}h,x)\right| \\&\le G(x).\end{aligned}

よってルベーグの収束定理より， $h\to 0$ とする(実際は $\{h_n\}$ を任意に取って $h_n\xrightarrow{n\to\infty}0$ とする)ことで，

F'(t) = \int_\mathbb{R}f_t(t,x)\,dx

であり，結論を得る。

証明終

なお，定理の主張は一般の測度空間 $(X,\mathcal{F},\mu)$ に対し， $f\colon I\times X\to\mathbb{R}$ を考え，

\frac{d}{dt}\int_X f(t,x)\,d\mu =\int_X \frac{\partial}{\partial t} f(t,x)\,d\mu

としても構いません。

微分と積分の交換の具体例

例題1.

$\displaystyle f(t)=\int_0^1 \sin tx\,dx$ のとき， $f'(t)$ を求めよ。

微分と積分の交換を認めれば， $\displaystyle f'(t)=\int_0^1 x\cos tx\,dx$ ですね。これは簡単で， $t\in\mathbb{R},\; 0\le x\le 1$ に対し，

\left|\frac{\partial}{\partial t} \sin tx \right|= |x\cos tx|\le 1

であり，右辺は可積分ですから，定理が使えます。

例題2.

$\displaystyle \operatorname{Re}\alpha >0,\; f(\alpha)=\int_0^\infty e^{-\alpha x^2}\,dx$ とする。 $f'(\alpha)$ を求めよ。

関数が複素数であることに注意してください(定理は実関数についてでした)。複素関数の場合，実の場合の証明で用いた平均値の定理を安易に使ってはいけません。今回は平均値の定理を用いない証明をしてみましょう。

例題2の解答

$M=\operatorname{Re} \alpha>0$ とし， $h\in\mathbb{C}$ を $\operatorname{Re} (\alpha+h)>M/2$ となるように取る。

\begin{aligned} \frac{f(\alpha+h)-f(\alpha)}{h} &= \int_0^\infty e^{-\alpha x^2}\frac{e^{-hx^2}-1}{h}\,dx \end{aligned}

であり，

\begin{aligned} \left|\frac{e^{-hx^2}-1}{h}\right|&=\left|\frac{1}{h}\int_0^h x^2 e^{-sx^2}\,ds \right| \\ &\le \frac{1}{|h|}\left| \int_0^h | x^2 e^{-sx^2} |\, ds \right|\\ &\le x^2 e^{Mx^2/2} \end{aligned}

なので， $\displaystyle \left| e^{-\alpha x^2}\frac{e^{-hx^2}-1}{h}\right|\le x^2 e^{-Mx^2/2}$ であり，右辺は $x\in(0,\infty)$ で可積分ですから， $h\to 0$ として

f'(\alpha) = -\int_0^\infty x^2e^{-\alpha x^2}\,dx

である。

関連する記事