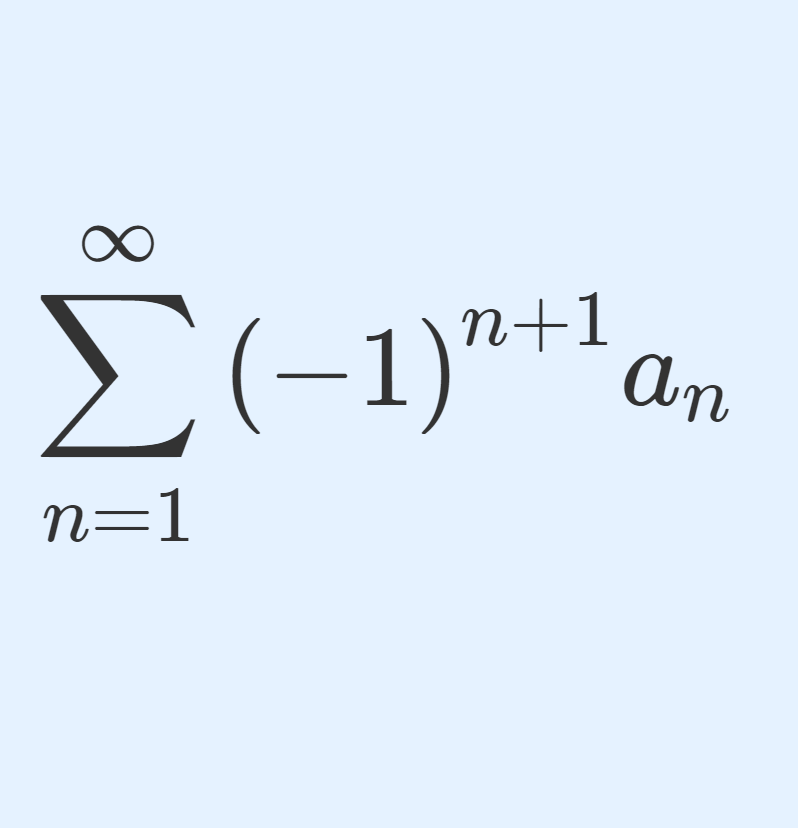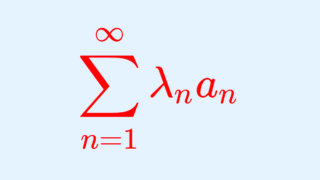交代級数の収束性の証明とその具体例

正の項と負の項が交互に現れる級数を交代級数 (alternating series) といいます。つまり， $a_n \ge 0 \,\, (n \ge 1)$ に対して，

\sum_{k=1}^n {(-1)}^{k+1} a_k = a_1 - a_2 + a_3 - \cdots + {(-1)}^{n+1} a_n

を交代級数といいます。今回は，ライプニッツの交代級数定理ともいわれる，級数に関する驚くべき定理を証明しましょう。

ライプニッツの交代級数定理
1. ライプニッツの定理の証明
2. 具体例
ライプニッツの定理の一般化
1. ちょっとした一般化
2. さらなる一般化～ディリクレの定理～
その他の「級数の収束」

ライプニッツの交代級数定理

定理（ライプニッツ; Leibniz ）

数列 $\{a_n\}$ は $a_n \ge 0$ をみたし，広義単調減少， $\lim_{n\to\infty} a_n =0$ であるとする。このとき，

\color{red}\sum_{n=1}^\infty {(-1)}^{n+1} a_n

は収束する。

証明は高校生でもおおむね理解できると思います。確認していきましょう。

ライプニッツの定理の証明

証明

$S_n = \sum_{k=1}^n (-1)^{n+1} a_n$ とおく。このとき $a_{2n-1} - a_{2n} \ge 0, \,- a_{2n} + a_{2n+1} \le 0$ であることと，

S_{2n} = \sum_{k=1}^n (a_{2k-1} - a_{2k}),\\ S_{2n+1} = a_1 + \sum_{k=1}^n (-a_{2k} + a_{2k+1})

であることより， ${S_{2n}}$ は単調増加， ${S_{2n+1}}$ は単調減少である。よって特に
$s_1 = \lim_{n\to\infty} S_{2n} \in [0, \infty],\\ s_2 = \lim_{n\to\infty} S_{2n+1} \in [-\infty, a_1]$
が存在する。
また， $a_{2n+1} = S_{2n+1} - S_{2n}$ の両辺 $n\to\infty$ として， $0 = s_2 - s_1$ より， $s_1 = s_2 \in [0, a_1]$ である（単に $s$ とかくことにする）。
以上から， $\lim_{n\to\infty}S_n = s$ となり，級数は収束する。

証明終

面白い定理ですが，証明はシンプルかもしれません。

具体例

具体例を２つ挙げてみます。

\log 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots

\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots

極限値の導出は，またの機会にしましょう。

ライプニッツの定理の一般化

この定理は，より一般の結果が知られています。それについて紹介しましょう。

ちょっとした一般化

定理

$\{a_n\}$ は単調減少かつ $a_n \xrightarrow{n\to\infty} 0$ とすると，

$\displaystyle \sum_{n=1}^\infty a_n \sin n \theta \, (\theta \in \mathbb{R} )$ は収束する。
$\displaystyle \sum_{n=1}^\infty a_n \cos n \theta \, (\theta \in \mathbb{R}\setminus \{2m\pi\mid m \in \mathbb{Z}\})$ は収束する。
$\displaystyle \sum_{n=1}^\infty a_n e^{in\theta} \, (\theta \in \mathbb{R}\setminus \{2m\pi\mid m \in \mathbb{Z}\})$ は収束する。

2.において， $\theta = \pi$ とすると， $\displaystyle \sum_{n=1}^\infty a_n \cos n \pi = \sum_{n=1}^\infty (-1)^n a_n$ となり，交代級数の収束の話になるため，上の3つは確かに一般化になっていますね。

さらに，これも含む一般化として，以下のようなものがあります。