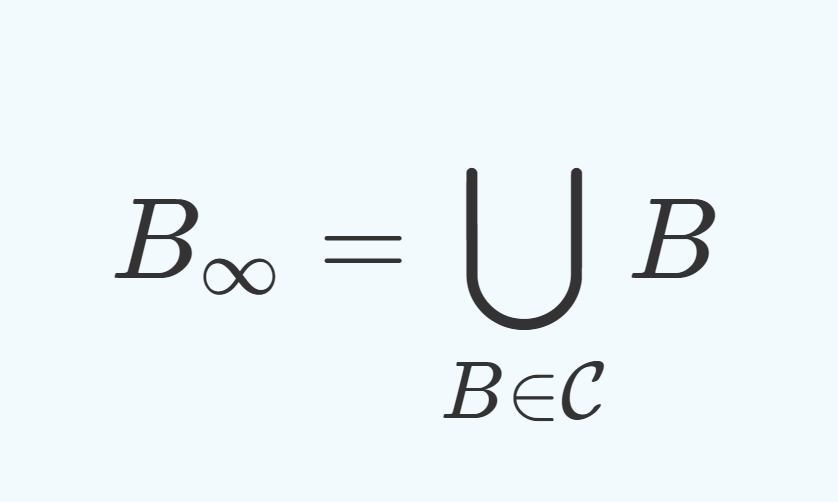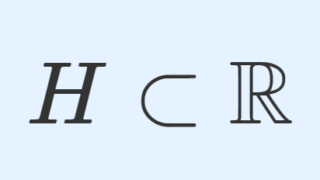任意のベクトル空間には,必ず基底が存在することを証明します。証明には,選択公理と同値なツォルンの補題を用います。
基底の存在定理
本定理は,選択公理を使って証明できる有名な定理の一つです。まず,基底が何かについて復習しておきましょう。
V を K 上ベクトル空間, 1 \le n \le \infty とする(すなわち無限も許す(非可算無限でも良い))。
\boldsymbol{v_1}, \boldsymbol{v_2}, \ldots \boldsymbol{v_n} \in V に対し,
- その任意の有限個が一次独立,すなわち有限個の k_{i_1},\dots, k_{i_l}\in K,\; \boldsymbol{v_{i_1}},\dots, \boldsymbol{v_{i_l}}\in V に対し,
\begin{aligned}&k_{i_1}\boldsymbol{v_{i_1}}+\cdots + k_{i_l}\boldsymbol{v_{i_l}}=\boldsymbol{0} \\ &\implies k_{i_1}=\cdots = k_{i_l}=0\end{aligned} - 任意の \boldsymbol{v}\in V に対し,ある有限個の k_{j_1},\dots, k_{j_m}\in K,\; \boldsymbol{v_{j_1}},\dots, \boldsymbol{v_{j_m}}\in V が存在して,
\boldsymbol{v}= k_{j_1}\boldsymbol{v_{j_1}}+\cdots + k_{j_m}\boldsymbol{v_{j_m}}
の両方が成立するとき, \boldsymbol{v_1}, \boldsymbol{v_2}, \ldots ,\boldsymbol{v_n} を v の基底 (basis) という。
基底について詳しくは以下で解説しています。
有限次元ベクトル空間においては,選択公理がなくとも,基底は明らかに存在します。それは,部分ベクトル空間の基底の延長により全体空間の基底が取れる証明で証明しています。
問題は,無限次元ベクトル空間でも基底が必ず存在するかということです。
基底の存在定理の証明
証明には,選択公理と同値なツォルンの補題を用います。ツォルンの補題とは,以下のようなものです。
帰納的半順序集合は極大元を持つ。
ここで,帰納的半順序集合とは,任意の全順序部分集合が上界を持つ半順序集合のことをいう。
証明
V\ne \{0\} をベクトル空間とする。
\small \mathcal{B}=\{ B\subset V \mid\text{any finite elements of } B \text{ are linearly independent}\}
と定める。すなわち, \mathcal{B} は「有限個の元が常に一次独立となる集合 B」全体を指すことにする。
ここで, \boldsymbol{v}\in V\setminus \{0\} に対して, \{\boldsymbol{v}\}\in \mathcal{B} であるから, \mathcal{B} は空でない。 \mathcal{B} は包含関係に対して半順序集合であるが,これが帰納的であることを示そう。
\mathcal{C}\subset \mathcal{B} を全順序部分集合とする。
B_\infty=\bigcup_{B\in \mathcal{C}} B
と定めると, B_\infty \in \mathcal{B} であることがわかる。
実際,有限個の元 \boldsymbol{v_1},\dots, \boldsymbol{v_n}\in B_\infty を任意に取ると, B_\infty の定義より,各 \boldsymbol{v_k} に対し, \boldsymbol{v_k} \in B_k となる B_k\in \mathcal{C} が存在する。 \mathcal{C} は全順序集合であるから, B_1\cup \dots \cup B_n \subset B_i となる i が存在する。\boldsymbol{v_1},\dots, \boldsymbol{v_n}\in B_i\in \mathcal{C}\subset \mathcal{B} であるから, \boldsymbol{v_1},\dots, \boldsymbol{v_n} は一次独立である。以上から, B_\infty \in \mathcal{B} が示せた。
したがって, \mathcal{B} の任意の全順序部分集合が上界を持つから, \mathcal{B} は帰納的半順序集合である。よって,ツォルンの補題から, \mathcal{B} は極大元 B^*\in \mathcal{B} をもつ。
このとき, B^* が基底である。実際, \boldsymbol{v}\in V が B^* の有限個の元の一次結合で表せないとすると, B^*\cup \{\boldsymbol{v}\}\in \mathcal{B} となって B^* の極大性に矛盾するからである。よって示せた。
証明終
無事証明できましたね。なお,逆に,任意のベクトル空間の基底の存在を認めると,選択公理が従うことが知られています。選択公理と,ベクトル空間の基底の存在定理は同値なわけですね。
関連する記事
本定理を用いて存在が分かる基底の代表例が,ハメル基底 (Hamel basis) でしょう。以下で解説しています。
他に,以下も関連する記事です。