内部(開核)・外部・境界について詳しく図解～距離空間・位相空間～

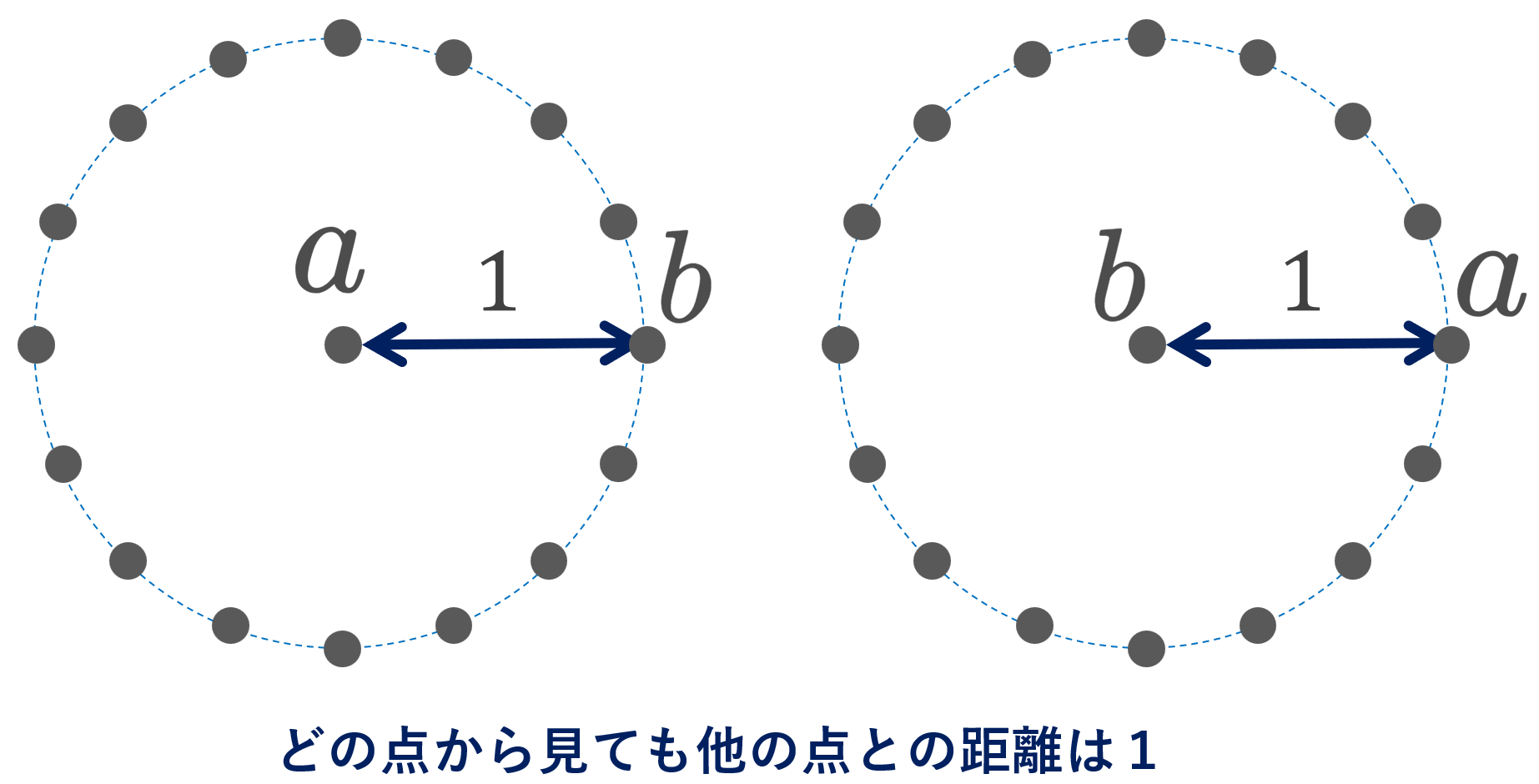
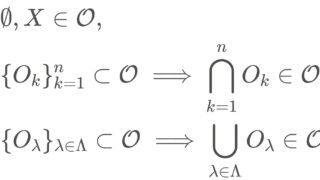集合の内点・外点・境界点と，その集合である内部(開核)・外部・境界について，具体例を用いながら詳しく図解していきます。まず，ユークリッド空間において考えることでイメージを膨らませ，それからより一般的な距離空間や位相空間における内部(開核)・外部・境界を考えます。

1. ユークリッド空間における内部(開核)・外部・境界
2. 距離空間における内部(開核)・外部・境界
3. 位相空間における内部(開核)・外部・境界
関連する記事

1. ユークリッド空間における内部(開核)・外部・境界

まずは，ユークリッド空間における内部(開核)・境界・外部を定義し，具体例を見ていきましょう。

$n$ 次元ユークリッド空間 $\R^n$ に対し，2点 $x=(x_1, \ldots, x_n), \, y = (y_1, \ldots , y_n)\in \R^n$ の距離は

\textcolor{red}{\large d(x, y)}=\sqrt{(x_1-y_1)^2+\cdots +(x_n-y_n)^2}

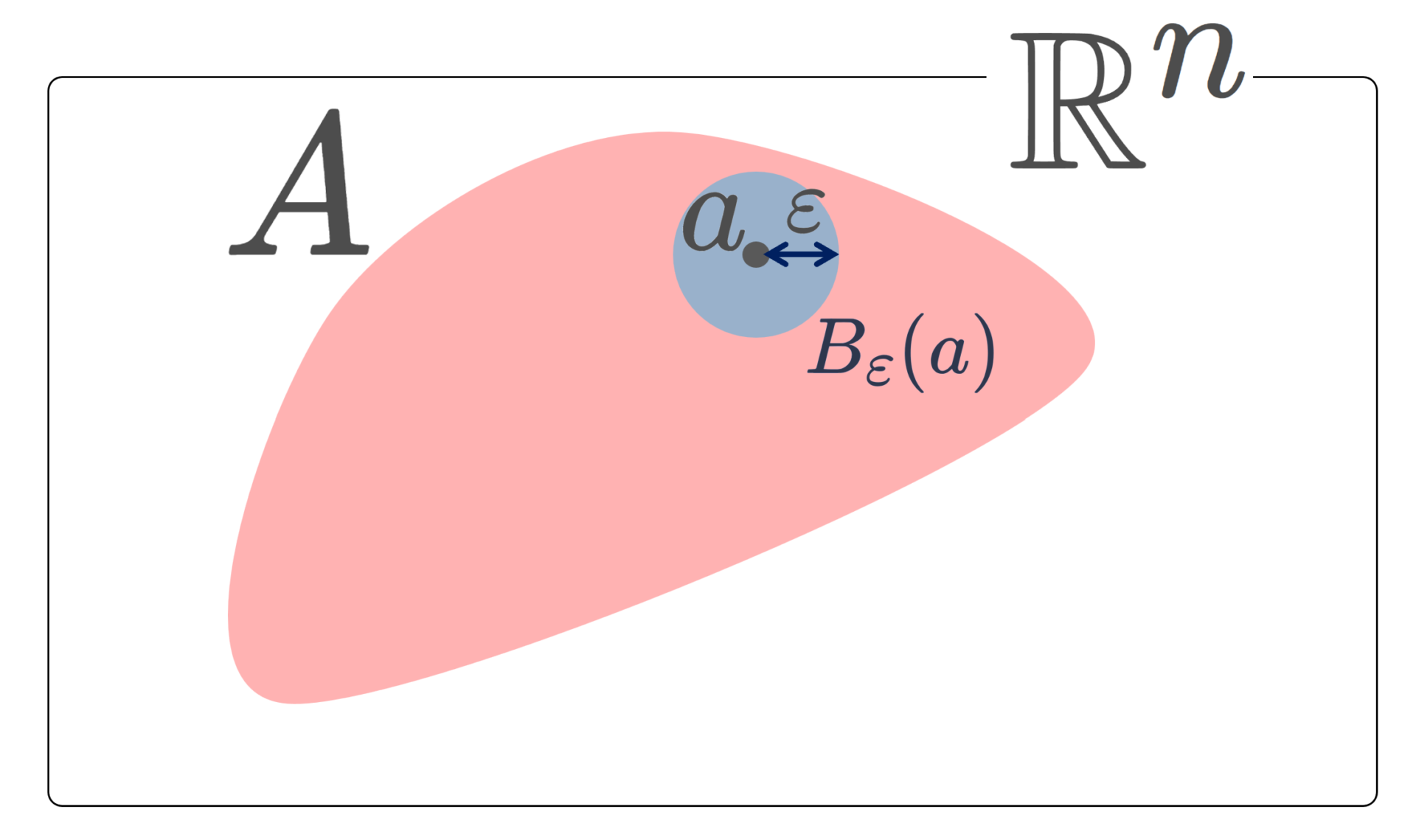
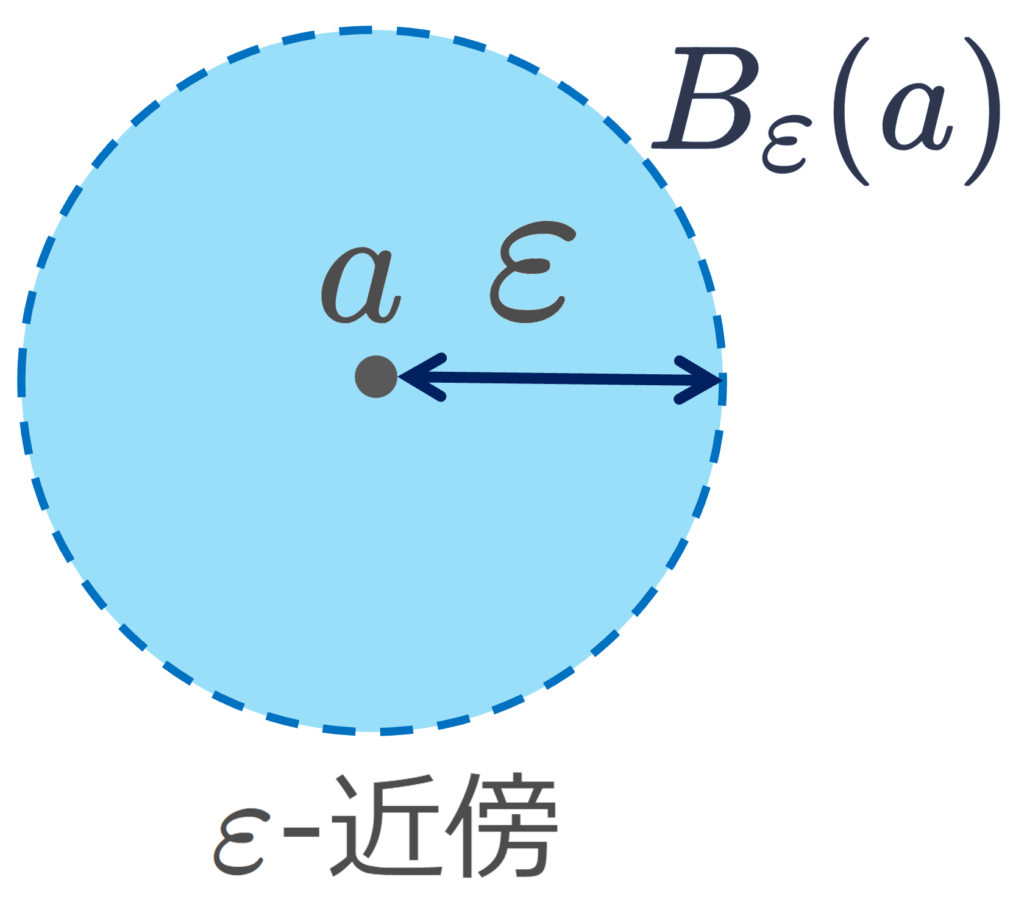
です。 $\varepsilon >0$ に対し，点 $a\in \R^n$ における $\varepsilon$ -近傍を

\textcolor{red}{\large B_\varepsilon(a)}=\{ x\in \R^n \mid d(a, x)<\varepsilon\}

とします。すなわち， $a\in \R^n$ と距離が $\varepsilon$ 未満の点の集合です。中心 $a$ 半径 $\varepsilon$ の $n$ 次元開球体といってもいいでしょう。

1.1 ユークリッド空間における内部(開核)

定義1.1（ユークリッド空間における内部(開核)）

$A\subset \R^n$ とする。

$a\in \R^n$ が以下の条件をみたすとき， $a$ は $A$ の内点 (interior point) という。

ある $\varepsilon >0$ が存在して，

\color{red}\Large B_\varepsilon(a) \subset A.

$A$ の内点全体の集合を $A$ の内部 (interior) または開核といい， $\large A^\circ$ または $\large A^i$ または $\color{red}\large \operatorname{Int}(A)$ とかく。

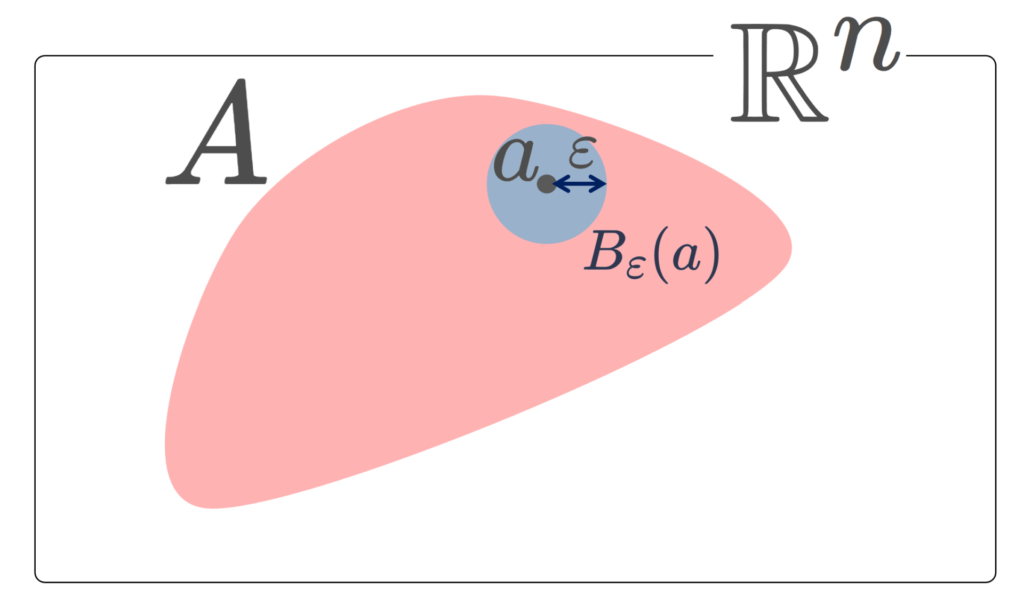
上の図で， $a$ は $A$ の内点です。

$a\in B_\varepsilon(a)$ ですから， $a$ が $A$ の内点なら $a\in A$ が成立します。よって， $\color{red}\operatorname{Int}(A)\subset A$ です。具体例を見てみましょう。

例1.1.1（ $\R$ その1）

$\R$ において，

開区間 $(0,1)$ の内部は $(0,1)$ そのものである。
閉区間 $[0,1]$ の内部は $(0,1)$ である。

すなわち，

$\operatorname{Int}\bigl((0,1)\bigr) = (0,1)$
$\operatorname{Int}\bigl([0,1]\bigr)=(0,1)$

である。

$a\in (0,1)$ とすると， $0< \varepsilon \le \min\{ a, 1-a\}$ とすることで，

(a-\varepsilon, a+\varepsilon)\subset (0,1)

とできます。 $(a-\varepsilon, a+\varepsilon)$ とは， $\R$ における $B_\varepsilon (a)$ のことです。よって，任意の $a\in (0,1)$ は内点と分かりますから， $(0,1)$ の内部は $(0,1)$ そのものです。

$[0,1]$ の内部について，上の議論より， $(0,1)$ が $[0,1]$ の内部に入るので，問題は2点 $0,1$ が $[0,1]$ の内点に入るか否かですが，これは否です。なぜなら，

(-\varepsilon , \varepsilon)\subset [0,1]

をみたす $\varepsilon>0$ は存在しないので， $0$ は内点ではないですし，

(1-\varepsilon , 1+\varepsilon)\subset [0,1]

をみたす $\varepsilon>0$ も存在しないので， $1$ も内点ではないからです。

例1.1.2（ $\R$ その2）

$-\infty<a<b<\infty$ とする。 $\R$ において，

$\operatorname{Int}\bigl((a,b)\bigr)=\operatorname{Int}\bigl([a,b]\bigr)=\operatorname{Int}\bigl([a,b)\bigr)=\operatorname{Int}\bigl((a,b]\bigr)=(a,b)$
$\operatorname{Int}\bigl(\R\bigr)=\R$
$\operatorname{Int}\bigl((-\infty, a)\bigr)=\operatorname{Int}\bigl((-\infty, a]\bigr)=(-\infty, a)$
$\operatorname{Int}\bigl( (a, \infty)\bigr)=\operatorname{Int}\bigl( [a, \infty)\bigr)= (a,\infty)$

例1.1と同様にすれば，どれもわかるはずです。2.については，一般に $\R^n$ の内部は $\R^n$ そのものといえます。

例1.1.3（ $\R$ その3）

$\R$ において，

$a\in\R$ に対し，1点集合 $\{a\}$ の内部は空集合 $\emptyset$ である。すなわち， $\operatorname{Int}\bigl(\{a\})=\emptyset$
有理数全体の集合 $\mathbb{Q}$ について， $\operatorname{Int}\bigl(\mathbb{Q}\bigr)=\emptyset$
$\operatorname{Int}\bigl( (0, 1)\cup [2,3]\bigr) =(0,1)\cup (2,3)$
$\operatorname{Int}\bigl([-1, 0)\cup \{1\}\cup [2,\infty)\bigr) = (-1, 0)\cup(2,\infty)$

1.について， $(a-\varepsilon, a+\varepsilon)\subset \{a\}$ をみたす $\varepsilon>0$ はありませんから， $a$ は $\{a\}$ の内点ではありませんね。

2.についても， $q\in \mathbb{Q}$ に対し， $(q-\varepsilon,q+\varepsilon)\subset \mathbb{Q}$ をみたす $\varepsilon >0$ はありませんから，任意の $q\in\mathbb{Q}$ は $\mathbb{Q}$ の内点ではありません。

例1.1.4（ $\mathbb{R}^2$ その1）

$\R^2$ について，

$s=(a,b)\in \R^2$ 中心，半径 $r>0$ の開円板
$\small \begin{aligned}&B_s(r)\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2< r^2\}\end{aligned}$
の内部は $B_s(r)$ そのものである。
$s=(a,b)\in \R^2$ 中心，半径 $r >0$ の閉円板
$\small \begin{aligned}&\overline{B_s(r)}\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2\le r^2\}\end{aligned}$
の内部は $B_s(r)$ である。
$a<b, \, c<d$ に対し， $\operatorname{Int}\bigl((a,b)\times (c,d)\bigr)=\operatorname{Int}\bigl([a,b]\times [c,d]\bigr)=\operatorname{Int}\bigl([a,b]\times (c,d)\bigr)=\operatorname{Int}\bigl((a,b]\times [c,d)\bigr)=(a,b)\times (c,d)$

ちょっとややこしいですが，1,2.における $(a,b)\in \R^2$ は点であり，3.における $(a,b)\times (c,d)\subset \R^2$ の $(a,b), (c,d)$ は $\R$ における開区間です。

例1.1.5（ $\mathbb{R}^2$ その2）

$\R^2$ について，

$\operatorname{Int}\bigl(\{ (x,\sin x)\mid x\in \R\} \bigr)=\emptyset$
$\operatorname{Int}\bigl(\{ (x,y)\in \R^2\mid y\ge 0\} \bigr)=\{ (x,y)\in \R^2\mid y> 0\}$

$\R^2$ において，曲線 $\{ (x, f(x))\mid x\in \R\}$ の内部は空集合です。

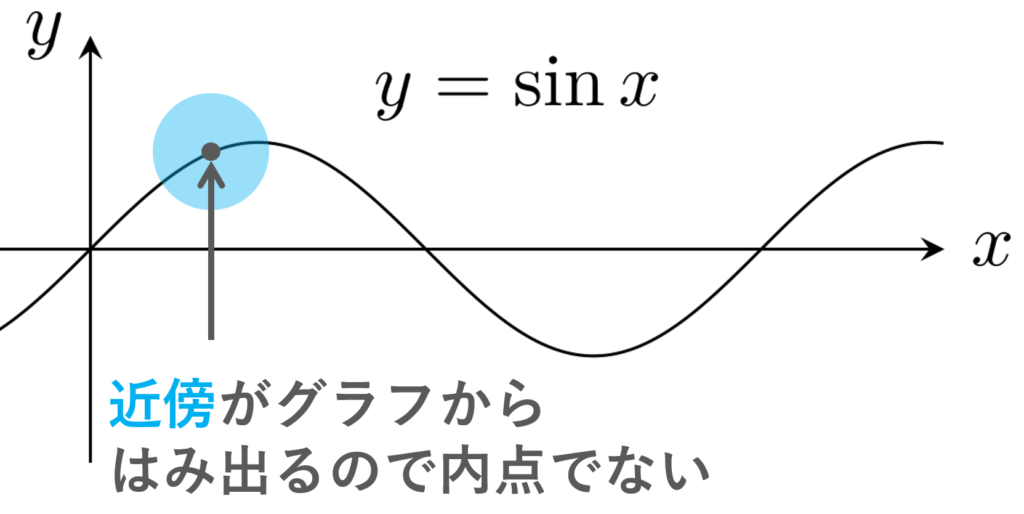
1.2 ユークリッド空間における外部

つづいて外部を定義しましょう。

定義1.2（ユークリッド空間における外部）

$A\subset \R^n$ とする。

$a\in \R^n$ が $A^c$ の内点であるとき， $a$ は $A$ の外点 (exterior point) であるという。

$A$ の外点全体の集合(すなわち $A^c$ の内部) を $A$ の外部 (exterior) といい， $\large A^e$ または $\color{red}\large \operatorname{Ext}(A)$ とかく。

定義より，

\large \color{red} \operatorname{Ext}(A) = \operatorname{Int}(A^c)

が成立します。

$B_\varepsilon(a)\subset A^c$ と $B_\varepsilon(a)\cap A=\emptyset$ は同じことです。 $B_\varepsilon(a)\subset A^c$ という式が， $a$ が $A^c$ の内点であることを表すので，外点は以下のように定義することもできます。

外点の定義の言いかえ

ある $\varepsilon>0$ が存在して，

\color{red}\Large B_\varepsilon(a)\cap A=\emptyset

となるとき， $a\in \R^n$ は $A$ の外点 (exterior point) であるという。

定義より， $a$ が $A$ の外点なら $a\in A^c$ です。よって， $\color{red} \operatorname{Ext}(A)\cap A=\emptyset$ が成り立ちます。

例1.2.1（ $\R$ その1）

$\R$ において，

$\operatorname{Ext}\bigl((0,1)\bigr) = (-\infty, 0)\cup (1,\infty)$
$\operatorname{Ext}\bigl([0,1]\bigr)=(-\infty, 0)\cup (1,\infty)$

である。

1.について，外部の定義より，

\begin{aligned}\operatorname{Ext}\bigl((0,1)\bigr) &=\operatorname{Int}\bigl((0,1)^c\bigr) \\ &= \operatorname{Int}\bigl((-\infty, 0]\cup [1,\infty) \bigr) \\ &= (-\infty, 0)\cup (1,\infty)\end{aligned}

ですね。2.も同じです。

例1.2.2（ $\R$ その2）

$\R$ において，

$\operatorname{Ext}\bigl(\{a\}\bigr) = (-\infty, a)\cup (a,\infty)$
$\operatorname{Ext}\bigl(\emptyset\bigr)=\R$
$\operatorname{Ext}\bigl(\mathbb{Q}\bigr)=\emptyset$
$\operatorname{Ext}\bigl([-1, 0)\cup \{1\}\cup [2,\infty)\bigr)=(-\infty, -1)\cup (0, 1)\cup (1,2)$

である。

例1.2.3（ $\R^2$ ）

$\R^2$ において，

$s=(a,b)\in \R^2$ 中心，半径 $r$ の開円板
$\small \begin{aligned}&B_s(r)\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2< r^2\}\end{aligned}$
あるいは閉円板
$\small \begin{aligned}&\overline{B_s(r)}\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2\le r^2\}\end{aligned}$
の外部は，どちらも
$\small \begin{aligned}&\bigl(\overline{ B_s(r)}\bigr)^c \\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2> r^2\}\end{aligned}$
である。
$S=\{ (x,\sin x)\mid x\in \R\}$ とすると， $\operatorname{Ext}(S)=\R^2\setminus S$
$\operatorname{Ext}\bigl(\{ (x,y)\in \R^2\mid y\ge 0\} \bigr)=\{ (x,y)\in \R^2\mid y< 0\}$

1.3 ユークリッド空間における境界

次に，境界について定義しましょう。

定義1.3（ユークリッド空間における境界）

$A\subset \R^n$ とする。

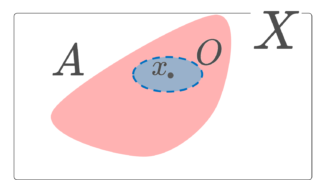
$a\in \R$ が $A$ の内点でも外点でもないとき， $a$ は $A$ の境界点 (boundary point) であるという。

$A$ の境界点全体の集合(すなわち $A$ の内部でも外部でもない点の集合)を $A$ の境界 (boundary, frontier) といい， $\large A^f$ または $\large\operatorname{bd}(A)$ または $\color{red}\large \partial A$ とかく。

定義より，

\large \partial A = \Bigl( \operatorname{Int}(A)\cup \operatorname{Ext}(A)\Bigr)^c

とかけます。また， $\partial A=\partial A^c$ であり，さらに

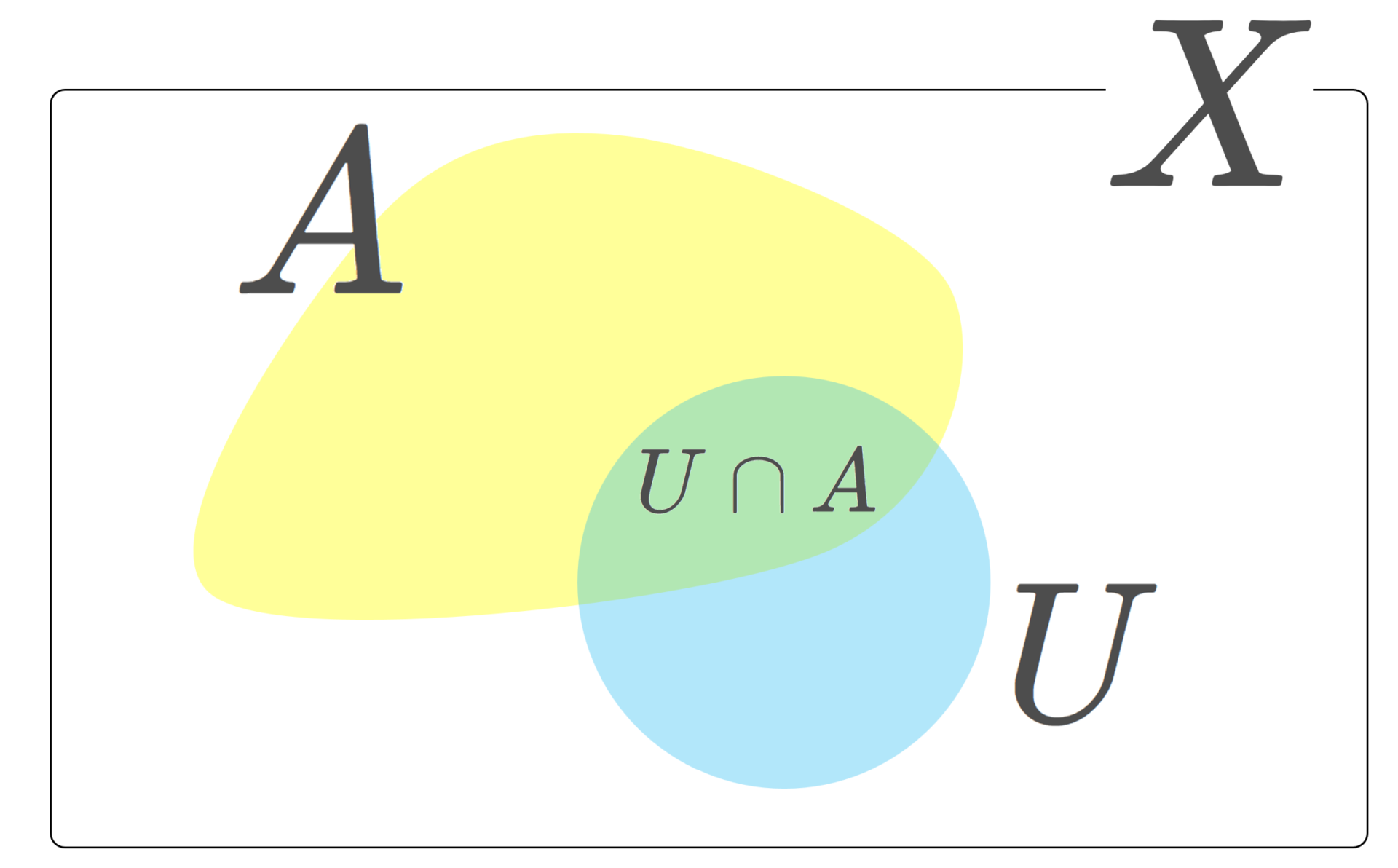
\color{red}\large X = \operatorname{Int}(A)\cup \partial A \cup \operatorname{Ext}(A)

のように，互いに交わらない3つの集合の和集合として， $X$ を分解することができます。

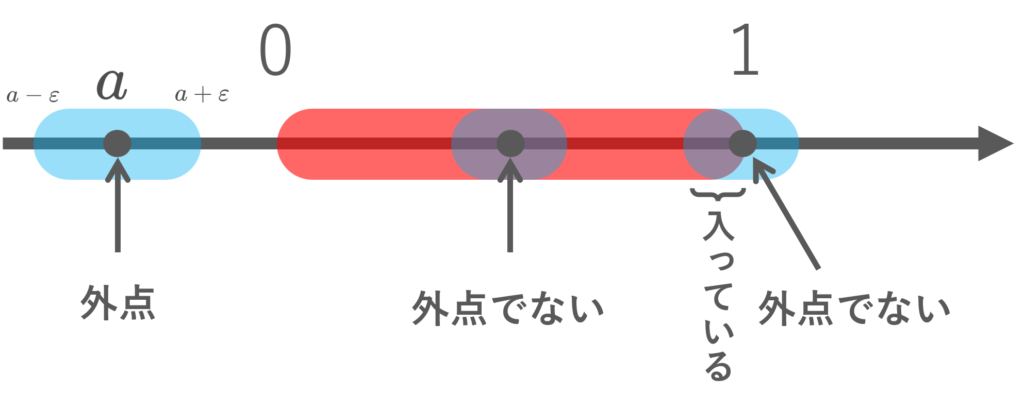
内点とは，「ある $\varepsilon >0$ が存在して $B_\varepsilon (a)\subset A$ 」でしたから，内点でないとは，「任意の $\varepsilon >0$ に対して $B_\varepsilon (a) \cap A^c \ne \emptyset$ 」となります。

同様に外点とは「ある $\varepsilon >0$ が存在して $B_\varepsilon (a)\subset A^c$ 」でしたから，外点でないとは，「任意の $\varepsilon >0$ に対して $B_\varepsilon (a) \cap A \ne \emptyset$ 」となります。

境界点とは，「内点でない」かつ「外点でない」ような点でしたから，境界点の定義は以下のように書き換えることができます。

境界点の定義の言いかえ

任意の $\varepsilon>0$ に対して，

\color{red}B_\varepsilon(a)\cap A\ne \emptyset\,\text{ and }\, B_\varepsilon(a)\cap A^c\ne \emptyset

となるとき， $a\in \R^n$ は $A$ の境界点 (boundary point) であるという。

内部・外部のときに用いた例をそのまま活用しましょう。内部でも外部でもない点が境界点です。

例1.3.1（ $\R$ ）

$\R$ において，

$\partial (0,1)=\partial [0, 1]=\{0, 1\}$
$\partial \{0\} = \{0\}$
$\partial \mathbb{Q}=\R$
$\partial \bigl([-1, 0)\cup \{1\}\cup [2,\infty)\bigr)=\{ -1, 0, 1, 2\}$

例1.3.2（ $\R^2$ ）

$\R^2$ において，

$s=(a,b)\in \R^2$ 中心，半径 $r$ の開円板
$\small \begin{aligned}&B_s(r)\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2< r^2\}\end{aligned}$
あるいは閉円板
$\small \begin{aligned}&\overline{B_s(r)}\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2\le r^2\}\end{aligned}$
の境界は，どちらも円周
$\small\{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2 =r^2\}$
である。
$S=\{ (x,\sin x)\mid x\in \R\}$ とすると， $\partial S= S$
$\partial \{ (x,y)\in \R^2\mid y\ge 0\} =\{ (x,0)\mid x\in \R\}$

1.4 ユークリッド空間における内部(開核)・外部・境界のまとめ

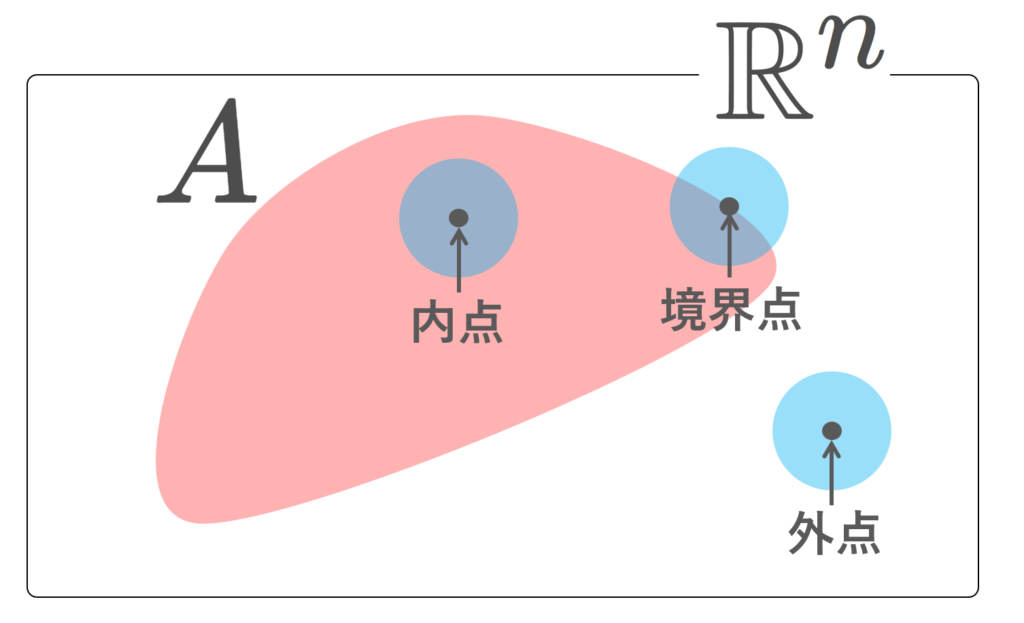
以下の図が分かりやすいでしょう。 $\varepsilon$ -近傍が $A$ 内に入るようにできるときは内点，逆に $A^c$ 内に入るようにできるときは外点，どんな $\varepsilon>0$ でも $A$ にも $A^c$ にも共有点をもつのが境界点です。

例もまとめておきましょう。

例1.4.1（ $\R$ ）

$\R$ において，

\small \begin{aligned} \operatorname{Int}\bigl( (0,1)\bigr)= \operatorname{Int}\bigl( [0,1]\bigr)&= (0,1), \\ \operatorname{Ext}\bigl((0,1)\bigr)=\operatorname{Ext}\bigl([0,1]\bigr)&= (-\infty, 0)\cup (1, \infty), \\ \partial (0,1)=\partial [0,1] &= \{0, 1\}\end{aligned}

\begin{aligned} \operatorname{Int}\bigl( \{a\}\bigr)&=\emptyset, \\ \operatorname{Ext}\bigl(\{a\} \bigr)&=(-\infty, a)\cup (a, \infty), \\ \partial \{a\} &=\{a\}\end{aligned}

\begin{aligned} \operatorname{Int}\bigl( (0,1)\cap\mathbb{Q}\bigr)&= \emptyset, \\ \operatorname{Ext}\bigl((0,1) \cap\mathbb{Q}\bigr)&= (-\infty, 0)\cup (1,\infty), \\ \partial \bigl((0,1)\cap\mathbb{Q} \bigr)&= [0,1] \end{aligned}

例1.4.2（ $\R^2$ ）

$\R^2$ において，

$s=(a,b)\in \R^2$ 中心，半径 $r$ の開円板
$\small \begin{aligned}&B_s(r)\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2< r^2\}\end{aligned}$
あるいは閉円板
$\small \begin{aligned}&\overline{B_s(r)}\\&= \{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2\le r^2\}\end{aligned}$
の内部・外部・境界は，それぞれ
$\begin{aligned}\small &\{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2 <r^2\},\\ &\{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2 >r^2\},\\ &\{ (x,y)\in \R^2\mid (x-a)^2+(y-b)^2 =r^2\}\end{aligned}$
である。
$S=\{ (x,\sin x)\mid x\in \R\}$ とすると，
$\begin{aligned}\operatorname{Int}(S) &= \emptyset, \\ \operatorname{Ext}(S) &=\R^2\setminus S,\\ \partial S&= S \end{aligned}$

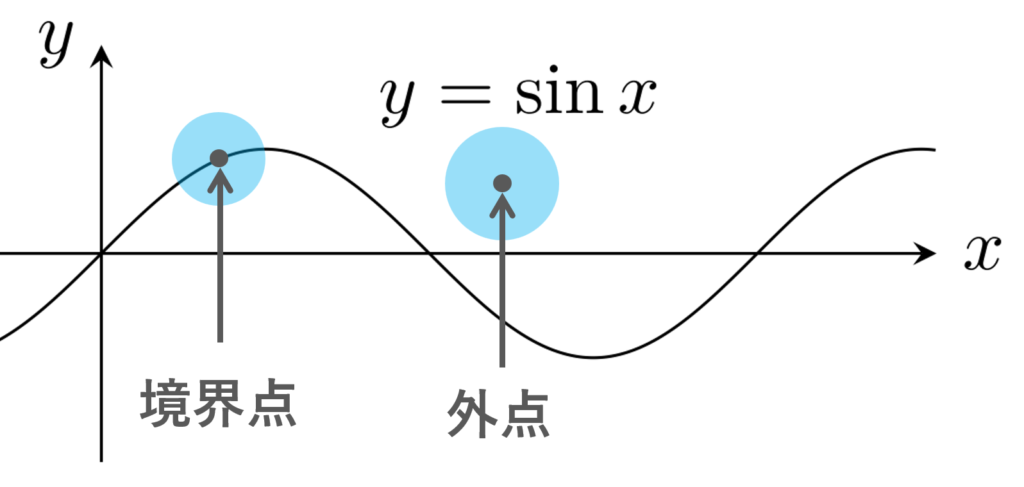
2. 距離空間における内部(開核)・外部・境界

距離空間における内部(開核)・境界・外部の定義はユークリッド空間と全く同じです。距離空間 $(X, d)$ において，

B_\varepsilon(a)=\{ x\in \R^n \mid d(a, x)<\varepsilon\}

を点 $a\in \R^n$ における $\varepsilon$ -近傍とします。

定義2（距離空間における内部(開核)・外部・境界）

$(X, d)$ を距離空間とし， $A\subset X$ とする。

$a\in X$ に対し，ある $\varepsilon>0$ が存在して， $\color{red}\large B_\varepsilon(a)\subset A$ とできるとき， $a$ を内点 (interior point) という。内点全体の集合を $A$ の内部 (interior) または開核という。
$A^c$ の内点を $A$ の外点 (exterior point) といい， $A$ の外点全体の集合を $A$ の外部 (exterior) という。
$A$ の内点でも外点でもない点を $A$ の境界点 (boundary point) といい， $A$ の境界点全体の集合を $A$ の境界 (boundary, frontier)

外部・境界について，ユークリッド空間のときに別の定義を紹介したように，距離空間においても全く同じです。単に $\R^n$ を距離空間 $X$ に変えるだけです。

外点・境界点の別の定義

$a\in X$ に対し，ある $\varepsilon>0$ が存在して，
$\color{red} A\cap B_\varepsilon(a) =\emptyset$
となるとき， $a$ は $A$ の外点 (exterior point)であるという。
$a\in X$ とする。任意の $\varepsilon >0$ に対し，
$\color{red} A\cap B_\varepsilon(a)\ne\emptyset \text{ and } A^c\cap B_\varepsilon(a)\ne\emptyset$
となるとき， $a$ は $A$ の境界点 (boundary point) であるという。

例2.1（離散距離）

$(X, d)$ を離散距離空間とする。すなわち， $a,b\in X$ に対し，

d(a,b)=\begin{cases} 0 &a=b, \\ 1 & a\ne b\end{cases}

である。このとき，任意の部分集合 $A\subset X$ に対し，

\begin{aligned} \operatorname{Int}(A)&=A, \\ \operatorname{Ext}(A)&= A^c,\\ \partial A &= \emptyset\end{aligned}

である。

$a\in A$ に対し， $B_{1/2}(a)=\{a\}$ なので，

a\in B_{1/2}(a)\subset A

とかけます。よって，任意の $a\in A$ は $A$ の内点です。ゆえに $\operatorname{Int}(A)=A$ です。同様に外点についても言えるので，内部でも外部でもない境界は空集合になります。

離散距離空間について詳しくは離散距離空間とは～定義と性質～で解説しています。

3. 位相空間における内部(開核)・外部・境界

位相空間には距離がありませんから， $\varepsilon$ -近傍という概念はなく，これまでと同じ定義ではいけません。ただし，内部(開核)さえ定義してしまえば，外部・境界の定義はこれまでと同じです。

シンプルな定義を紹介します。

定義3.1（位相空間における内部(開核)）

$X$ を位相空間とし， $A\subset X$ とする。

$A$ に含まれる最大の開集合を $A$ の内部 (interior) または開核といい， $\large A^\circ$ または $\large A^i$ または $\color{red}\large \operatorname{Int}(A)$ とかく。

内部に属する各点を内点 (interior point) という。

$\{O_\lambda\}_{\lambda\in \Lambda}$ を $A$ に含まれる開集合全体の集合としたとき， $\bigcup_{ \lambda\in \Lambda} O_\lambda$ も $A$ に含まれる開集合ですから，これが「 $A$ に含まれる最大の開集合」です。

ちょっと定義の雰囲気がユークリッド空間・距離空間のときと違うと思ったかもしれません。ただ，今はシンプルな定義を紹介したので，もう少しユークリッド空間・距離空間のときの定義に寄せたものも述べておきましょう。

位相空間における内部(開核)のユークリッド空間・距離空間に寄せた定義

$X$ を位相空間とし， $A\subset X$ とする。

$a\in A$ に対し，ある開集合 $O$ が存在して，

\color{red}\large a\in O\subset A

とできるとき， $a$ は $A$ の内点 (interior point) といい，内点全体の集合を内部 (interior) という。

ユークリッド空間・距離空間では $\varepsilon$ -近傍 $B_\varepsilon (a)$ だったものが，開集合 $O$ に変わっています。位相空間にも近傍の概念はありますから，定義において，「開集合」ではなく「近傍」にしても大丈夫です（が，位相空間の定義は開集合から出発することが多く，開集合にした方が分かりやすいと思うので，いまは「開集合」にしています）。

内部(開核)さえ定義してしまえば，外部・境界の定義はユークリッド空間・距離空間のときと同じです。

定義3.2（位相空間における外部・境界）

$A^c$ の内点を $A$ の外点 (exterior point) といい， $A$ の外点全体の集合を $A$ の外部 (exterior) という。
$A$ の内点でも外点でもない点を $A$ の境界点 (boundary point) といい， $A$ の境界点全体の集合を $A$ の境界 (boundary, frontier) という。

具体例を挙げておきましょう。

例3.1（ $\mathbb{Q}$ に相対位相を入れたもの）

有理数全体 $\mathbb{Q}$ に $\R$ の相対位相(距離から定まる自然な位相)を入れた位相空間について，

\begin{aligned} \operatorname{Int}\bigl( (0,\sqrt{2})\cap\mathbb{Q}\bigr)&= (0,\sqrt{2})\cap\mathbb{Q}, \\ \operatorname{Ext}\bigl((0,\sqrt{2}) \cap\mathbb{Q}\bigr)&= \bigl( (-\infty, 0)\cup (\sqrt{2}, \infty) \bigr)\cap \mathbb{Q}, \\ \partial (0,\sqrt{2})\cap\mathbb{Q} &= \{0\}\end{aligned}

である。

$\R$ においては，

\begin{aligned} \operatorname{Int}\bigl( (0,\sqrt{2})\cap\mathbb{Q}\bigr)&= \emptyset, \\ \operatorname{Ext}\bigl((0,\sqrt{2}) \cap\mathbb{Q}\bigr)&= (-\infty, 0)\cup (\sqrt{2},\infty), \\ \partial \bigl((0,\sqrt{2})\cap\mathbb{Q} \bigr)&= [0,\sqrt{2}] \end{aligned}

ですから，その違いに注意してください。

例3.2（ $\R$ に異なる位相を入れたもの）

$\mathcal{O}=\{(-\infty, a)\mid a\in \R\}\cup\{ \emptyset, \R \}$ とすると， $(\R,\mathcal{O})$ は位相空間になる。このとき，

\begin{aligned} \operatorname{Int}\bigl( (0,1)\bigr)&= \emptyset, \\ \operatorname{Ext}\bigl((0,1) \bigr)&= (-\infty, 0), \\ \partial (0,1) &= [0, \infty) \end{aligned}

また，

\begin{aligned} \operatorname{Int}\bigl( (-\infty, 0)\bigr)&= (-\infty, 0) \\ \operatorname{Ext}\bigl((-\infty, 0) \bigr)&= \emptyset, \\ \partial (-\infty, 0) &= [0, \infty) \end{aligned}

である。

最後に，内部(開核)の基本的性質についていくつか紹介しておきます。

定理（内部(開核)の性質）

$(X, \mathcal{O})$ を位相空間とし， $A, B\subset X$ とする。このとき，

$\operatorname{Int}(\emptyset)=\emptyset, \quad \operatorname{Int}(X) = X.$
$\operatorname{Int}(A)\subset A.$
$\operatorname{Int}(\operatorname{Int}(A))=\operatorname{Int}(A).$
$\operatorname{Int}(A\cap B) = \operatorname{Int}(A)\cap \operatorname{Int}(B).$

1.から3.は定義から明らかです。4.のみ証明しましょう。

4.の証明

$\operatorname{Int}(A)\cap \operatorname{Int}(B)$ は開集合であり，かつ $\operatorname{Int}(A)\cap \operatorname{Int}(B)\subset A\cap B$ が成り立つから， $\operatorname{Int}(A)\cap \operatorname{Int}(B)\subset \operatorname{Int}(A\cap B)$ である。

また， $A\cap B\subset A$ より， $\operatorname{Int}(A\cap B)\subset \operatorname{Int}(A)$ であり，同様に $\operatorname{Int}(A\cap B)\subset \operatorname{Int}(B)$ でもあるから， $\operatorname{Int}(A\cap B)\subset \operatorname{Int}(A)\cap \operatorname{Int}(B)$ が言える。よって題意は示された。

証明終

注意ですが， $\operatorname{Int}(A\cup B) \supset \operatorname{Int}(A)\cup \operatorname{Int}(B)$ であり，これは必ずしも $=$ にはなりません。

実際， $A\cup B\supset A$ より， $\operatorname{Int}(A\cup B)\supset \operatorname{Int}(A)$ であり，同様に $\operatorname{Int}(A\cup B)\supset \operatorname{Int}(B)$ なので， $\operatorname{Int}(A\cup B)\supset \operatorname{Int}(A)\cup \operatorname{Int}(B)$ がいえます。

一方で $A =(0,1),\; B=[1,2)$ とすると，