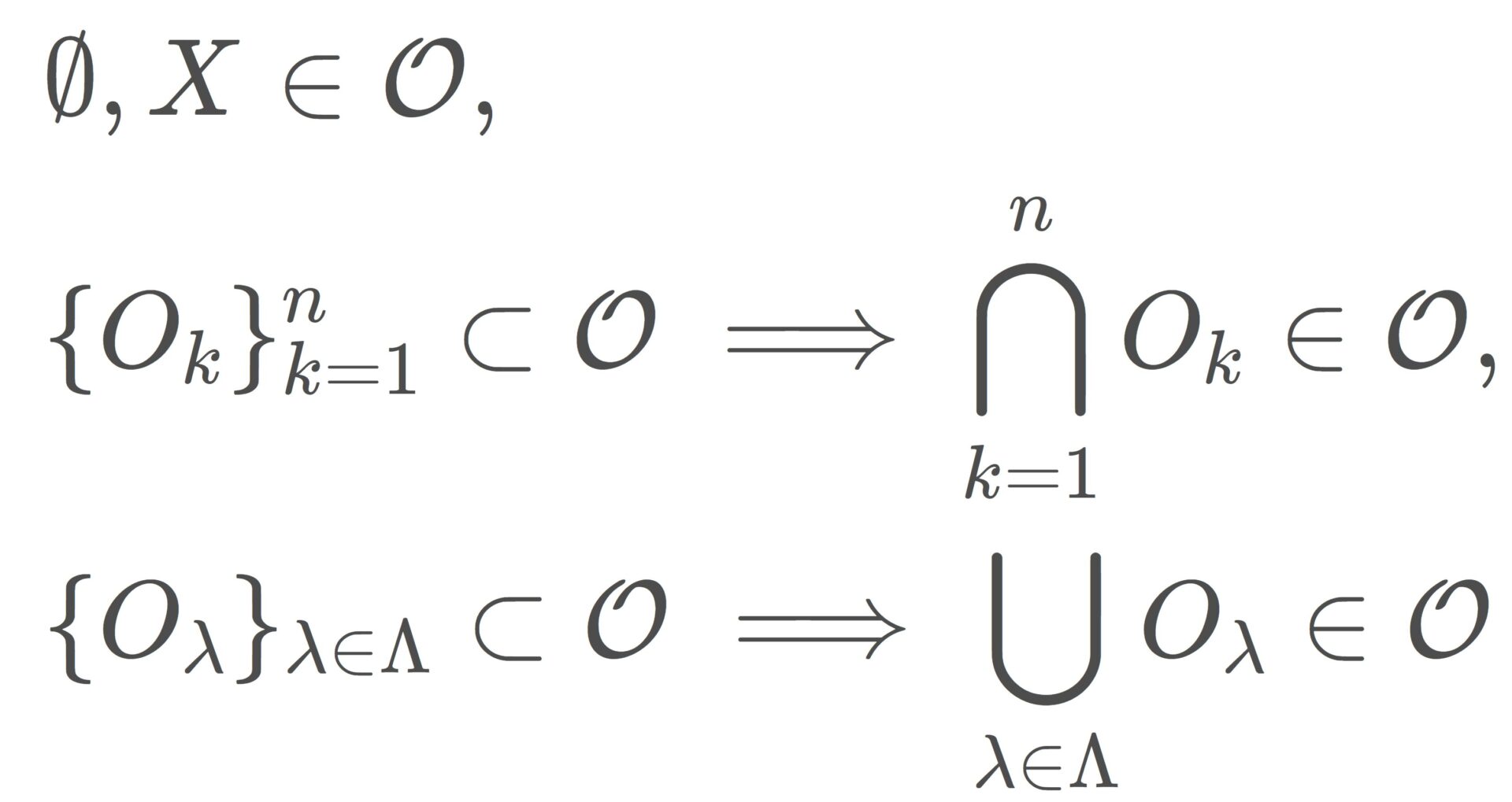位相空間とは，点の近さを土台とする「収束性・写像の連続性」が議論できる抽象的な空間といえます。その定義はかなり抽象的なものですが，ユークリッド空間や距離空間でなくても，さらに一般的に広く収束・連続の概念を取り扱うことができ，大学以上の数学を深めるうえで欠かすことのできない概念です。
位相空間と，位相空間における「開集合・閉集合」の概念について，具体的な言葉での説明を交えながらその概要を紹介します。
位相空間の定義と例
早速，位相空間を定義していきましょう。位相空間の定義の仕方はいろいろありますが，一番オーソドックスな，開集合系を用いた定義を用います。「開集合」という言葉は，もう少し後で出てくるので，今は気にしなくてよいです。
開集合系を用いた位相空間の定義
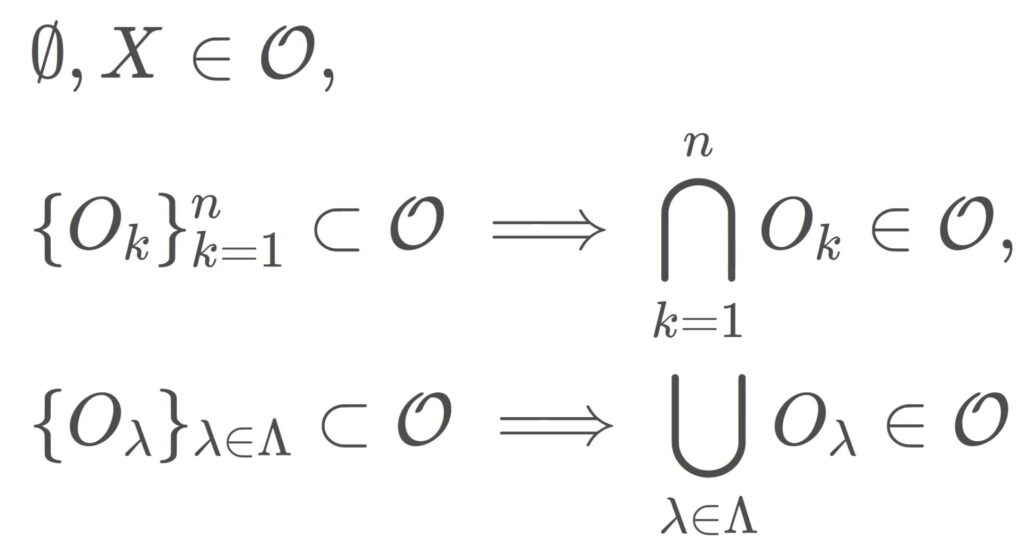
以下で， 2^X は X のべき集合，すなわち部分集合の集合です。
定義（位相空間）
X を空でない集合とする。X の部分集合の族 \mathcal{O}\subset 2^X が次の条件をすべて満たすとき，集合 X の位相 (topology) であるという。
- \color{red} \emptyset \in \mathcal{O},\; X\in\mathcal{O}.
- O_1, O_2, \ldots, O_n \in \mathcal{O} のとき， \color{red}\bigcap_{k=1}^n O_k \in \mathcal{O}.
- \{O_\lambda\}_{\lambda\in \Lambda} \subset \mathcal{O} とするとき， \color{red} \bigcup_{\lambda\in \Lambda} O_\lambda \in\mathcal{O}.
位相 \mathcal{O} が備わった集合 X ( (X, \mathcal{O}) とかくこともある)を位相空間 (topological space) という。
2.は有限個の共通部分で閉じているといっているのに対し，3.は和集合で閉じているといっています。3.については，無限個，とくに非可算無限個であってもかまいません。
2.の定義は，
\color{red} O_1, O_2\in \mathcal{O}\implies O_1\cap O_2\in \mathcal{O}といってもかまいません。2個で言えれば，帰納的に有限個で言えるからです。
定義がいくぶん抽象的に感じたと思います。「収束性・連続性の概念」それのみを一般化したものですから，具体的なものは全て削ぎ落しているため，仕方ありません。「近傍（きんぼう）」という概念があり，点の近さを議論することは可能ですが，距離空間のように，点同士の近さを表すのに具体的な数値があるわけではありません。
具体例を通して，定義を理解していきましょう。
位相空間の例
位相空間の例1（密着空間）
空でない集合 X に対し，\mathcal{O}=\{ \emptyset, X\} と定めると， \mathcal{O} は位相空間となる。これを密着位相 (indiscrete topology, trivial topology) といい， (X, \mathcal{O}) を密着空間 (indiscrete space, trivial space) という。
密着空間とは，開集合が少なく，すべての点が位相的に「密着」していて区別できないような空間です。X が2点以上の集合のとき，収束の議論をしようにも，収束の一意性が保証されません。また，連続写像 f\colon X\to \R は定数関数しかないことが知られています。点を区別して「収束・連続」の議論ができない空間なのです。
位相空間の例2（離散空間）
空でない集合 X に対し，\mathcal{O}=2^X ( X のべき集合)と定めると， \mathcal{O} は位相空間となる。これを離散位相 (discrete topology) といい， (X, \mathcal{O}) を離散空間 (discrete space) という。
今度は逆で，開集合が多すぎるため，すべての点を区別できてしまい，「離れている」ような空間です。「離れている」ため，x\in X に収束する列(有向点列)は最終的に x,x,x,x,\ldots とならなければなりませんし，また，どんな写像でも f\colon X\to \R は連続写像になります。点が区別されすぎてしまうため，「いい感じに近い点」が取れないような空間なのです。
例1,2を通して，位相 \mathcal{O} は「細かすぎても」「粗すぎても」良いというものではないことが分かりました。
位相空間の例3（距離空間の位相）
(X, d) を距離空間とする。このとき，距離空間における開集合系（開集合たちの集合）は位相空間の定義をみたす。よって，距離空間はその開集合系により位相空間とみなせる。この位相を距離空間から定まる位相を自然な位相 (natural topology) または通常の位相 (usual topology) という。
U\subset X が距離空間における開集合であるとは，任意の x\in U に対し，ある \varepsilon >0 が存在して， B_\varepsilon(x)\subset U とできることを言います。ただし， B_\varepsilon(x)=\{ y\in X \mid d(x,y)<\varepsilon\} は x の \varepsilon-近傍です。
距離空間は位相空間と思えるということです。これにより，ユークリッド空間 \R^d も位相空間と思えるし，ノルム空間(ノルムが定まったベクトル空間)も位相空間と思えます。
なお，「距離空間としては別物でも，位相空間としては同じもの」ということがあります。ものすごく簡単な例では，たとえば， (X, d) と (X, 2d) は距離空間としては別物（等長同型でない）ですが，定まる位相は同じです。この例は簡単すぎますが，他にも， \R^n におけるユークリッド距離とマンハッタン距離が定まる位相も同じです。位相空間は距離空間よりも一般的で，より抽象度が上がったものといえるわけです。
位相空間の例4（補有限位相）
X を空でない集合とし，
\mathcal{O}=\{ A\subset X\mid A=\emptyset \text{ or } A^c\text{ is finite}\}
とすると， \mathcal{O} は位相空間の定義を満たす。 \mathcal{O} を補有限位相 (cofinite topology) という。
補有限位相が位相空間の定義を満たすことを確認してみてください。
逆に， X が無限集合のとき， \mathcal{O}=\{ A\subset X\mid A=X \text{ or } A\text{ is finite}\} とはできません。位相空間の定義を満たさないからです。これも確認してみましょう。
位相空間における開集合・閉集合
先ほど，「開集合系」を用いて位相空間を定義しましたが，ここでいう「開集合系」とは，開集合たちの集まり \mathcal{O} をつかって定義するということです。
位相空間における開集合・閉集合の定義
定義（開集合・閉集合）
(X,\mathcal{O}) を位相空間とする。
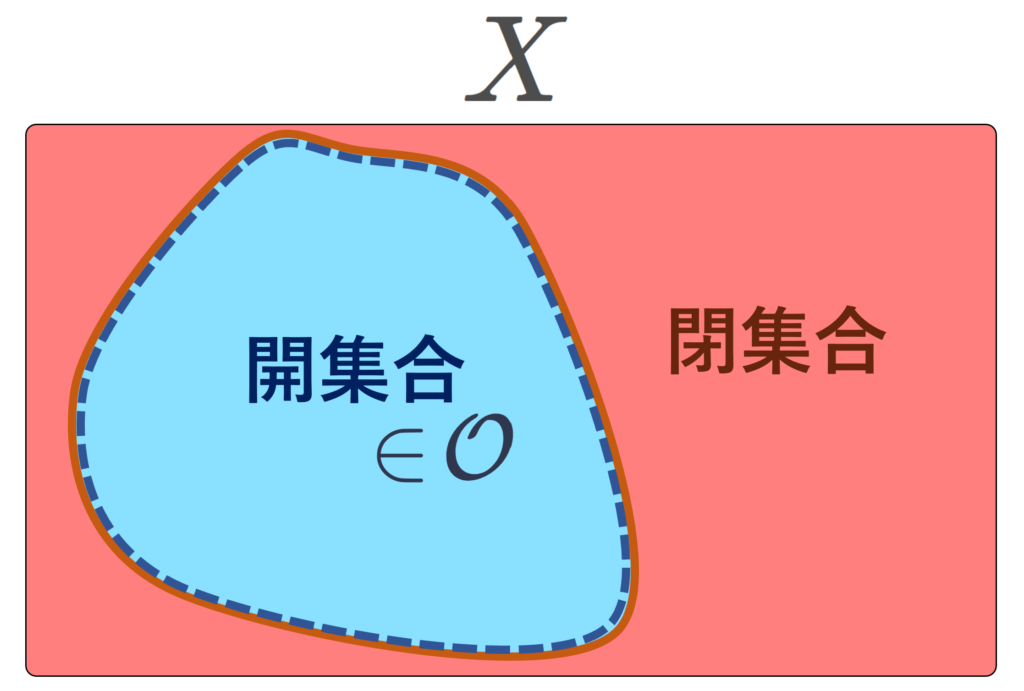
\mathcal{O} の元となる X の部分集合を開集合 (open set) という。すなわち， A\subset X が A\in \mathcal{O} をみたすとき， A を開集合という。
\mathcal{O} の元の補集合となる X の部分集合を閉集合 (closed set) という。すなわち， F\subset X が F^c\in\mathcal{O} をみたすとき， F を閉集合という。
開集合の補集合が閉集合であり，閉集合の補集合が開集合です。
これにより， X の部分集合は，次の4通りに分けられることになります。
- 開集合かつ閉集合
- 開集合であるが閉集合でない
- 閉集合であるが開集合でない
- 開集合でも閉集合でもない
位相空間の定義から， \emptyset と X は必ず開集合だし，X=\emptyset^c,\, \emptyset = X^c なので，閉集合でもあります。よって， \emptyset , X は開集合かつ閉集合です。
位相空間における開集合・閉集合の例
開集合・閉集合の例1（密着空間）
(X, \mathcal{O}) が密着空間のとき， \emptyset, X 以外のすべての部分集合が開集合でも閉集合でもない。
\mathcal{O}=\{ \emptyset, X\} ですから，そうですね。
開集合・閉集合の例2（離散空間）
(X, \mathcal{O}) が離散空間のとき，すべての部分集合が開集合かつ閉集合である。
\mathcal{O}=2^X ですから， X のすべての部分集合が開集合になります。また，どんな部分集合であっても，その補集合は開集合ですから，その部分集合自体は閉集合と言えます。
開集合・閉集合の例3（\R）
\R に自然な位相を入れた位相空間は， \emptyset, \R のみが「開集合かつ閉集合」であり，その他の部分集合は「開集合であるが閉集合でない」「閉集合であるが開集合でない」「開集合でも閉集合でもない」のいずれかとなる。
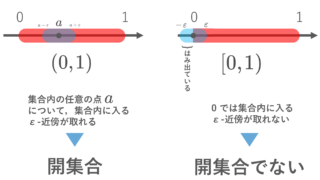
たとえば， a<b に対し， (a,b) は開集合であるが閉集合でない， [a,b] は閉集合であるが開集合でない， (a,b], [a,b) は開集合でも閉集合でもない。
また，1点集合 \{x\}\subset \R は閉集合であって開集合でない。
「開集合かつ閉集合」となるのが \emptyset, \R だけであるという説明は，ここでは省略します。より一般に，「開集合かつ閉集合」となるのが \emptyset, X のみである位相空間 (X, \mathcal{O}) を連結空間 (connected space) といいます。
\R において， \bigcap_{n=1}^\infty (-1/n, 1/n) =\{0\} ですが， \{0\} は開集合ではありません。これは，開集合は無限個の共通部分で閉じていなくてよいことを表しています。
開集合・閉集合の例4（補有限位相）
X を無限集合とし，\mathcal{O} を補有限位相とする。
このとき， \emptyset, X は開集合かつ閉集合で， \emptyset, X を除くすべての無限部分集合は「開集合であるが閉集合でない」， \emptyset, X を除くすべての有限部分集合は「閉集合であるが開集合でない」となる。
位相空間のその他の定義
位相空間には，最初に述べた開集合系を用いた定義とは別に，それと同値な定義があります。紹介しておきましょう。
閉集合系を用いた位相空間の定義
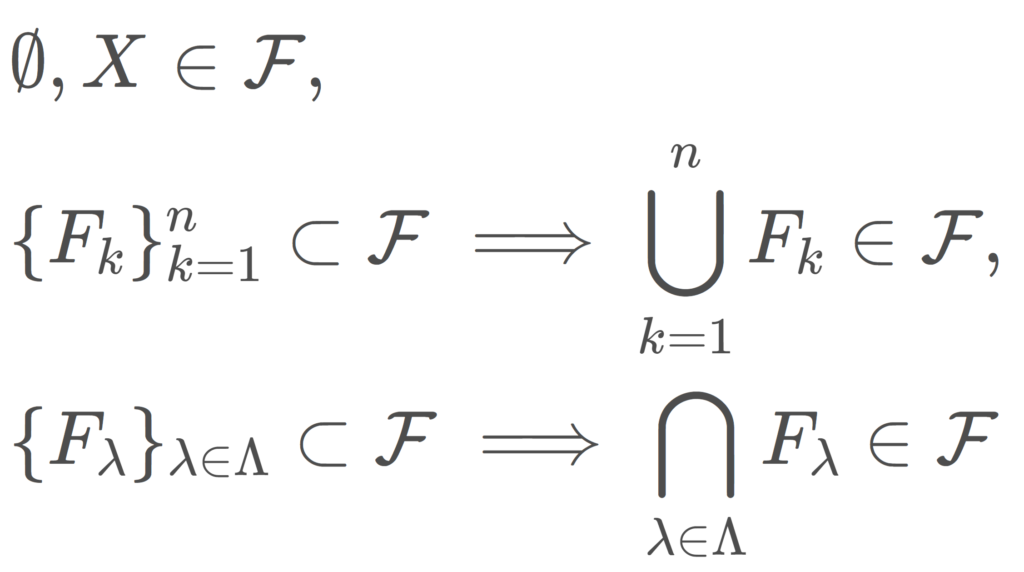
ド・モルガンの法則より， \begin{aligned} \left(\bigcap_{k=1}^n O_k\right)^c &= \bigcup_{k=1}^n {O_k}^c, \\ \left(\bigcup_{\lambda\in \Lambda} O_\lambda \right)^c &= \bigcap_{\lambda\in \Lambda} {O_\lambda}^c\end{aligned}
なので，開集合の代わりにその補集合である閉集合を用いて定義しても，位相空間は定義できます。
定義（閉集合系を用いた位相空間）
X を空でない集合とする。X の部分集合の族 \mathcal{F}\subset 2^X が次の条件をすべて満たすとき， (X, \mathcal{F}) を， \mathcal{F} を閉集合系とする位相空間 (topological space) といい， \mathcal{F} に属する集合を閉集合 (closed space) という。
- \color{red} \emptyset \in \mathcal{F},\; X\in\mathcal{F}.
- F_1, F_2, \ldots, F_n \in \mathcal{F} のとき， \color{red}\bigcup_{k=1}^n F_k \in \mathcal{F}.
- \{F_\lambda\}_{\lambda\in \Lambda} \subset \mathcal{F} とするとき， \color{red} \bigcap_{\lambda\in \Lambda} F_\lambda \in\mathcal{F}.
閉集合は有限個の和集合について閉じていて，非可算無限個の共通部分について閉じていますね。
近傍系を用いた位相空間の定義
最後に，ここまでとはちょっと違う位相空間の定義の仕方を紹介しておきましょう。
位相空間には，近傍という概念があります。これが，位相空間における点同士の近さを議論する概念です。ふつうは開集合を定義して，そこから近傍を定義するのですが，逆にその近傍を出発点として，位相空間を定めます。
定義（近傍系を用いた位相空間; ハウスドルフの公理系）
X を空でない集合とする。各 x\in X について定まっている部分集合の族 \mathcal{N}(x)\subset 2^X が次の条件をすべて満たすとき， \mathcal{N}(x) を x の近傍系といい， \mathcal{N}(x) の元となる集合を x の近傍 (neighbourhood) という。
- X\in \mathcal{N}(x).
- U\in \mathcal{N}(x) ならば x\in U.
- U_1, U_2, \ldots, U_n \in \mathcal{N}(x) ならば，\bigcap_{k=1}^n U_k \in \mathcal{N}(x).
- U\in \mathcal{N}(x) かつ U\subset V\subset X ならば V\in \mathcal{N}(x).
- 任意の U\in \mathcal{N}(x) に対し，ある V\in\mathcal{N}(x) が存在して，任意の y\in V に対し， U\in\mathcal{N}(y) とできる。
(X, \mathcal{N}) を， \mathcal{N}(x) を近傍系とする位相空間 (topological space) という。
開集合系を
\mathcal{O}= \{ N\subset X\mid \forall x\in N,\, N\in\mathcal{N}(x)\}
と定義することで，\mathcal{O} を開集合系とする位相空間が得られ，この位相空間は，上の \mathcal{N}(x) を近傍系とすることがわかります。また，上の \mathcal{N}(x) を近傍系とする位相空間はただ一つであることが知られています。詳しい説明は省略します。
位相空間の定義からその先へ
本記事では，位相空間を定義しましたが，この先，位相空間における基本的な概念を列挙しておきましょう。
- 内部(開核)・外部・境界
- 閉包
- 集積点・孤立点
- 相対位相・ 部分位相空間
- 近傍・基本近傍系
- 連続写像
- ネット（有向点族・有向点列）
- フィルター
- コンパクト空間
- 可分空間
- 連結空間
- 第一可算・第二可算
- ハウスドルフ空間
- 正規空間
- 正則空間
- 他
