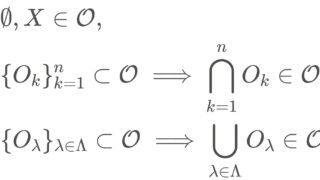ユークリッド空間・距離空間における開集合・閉集合とは,ものすごく崩して言うと, \R における開区間・閉区間をより一般の集合で考えたようなものです。開集合・閉集合について定義し,その例を紹介します。
ユークリッド空間における開集合・閉集合
定義の仕方はいろいろありますが,個人的に一番イメージしやすいものを採用し,その後に詳細に掘り下げて別の定義も紹介する流れにします。
n 次元ユークリッド空間 \R^n に対し,2点 x=(x_1, \ldots, x_n), \, y = (y_1, \ldots , y_n)\in \R^n の距離は
\textcolor{red}{\large d(x, y)}=\sqrt{(x_1-y_1)^2+\cdots +(x_n-y_n)^2}
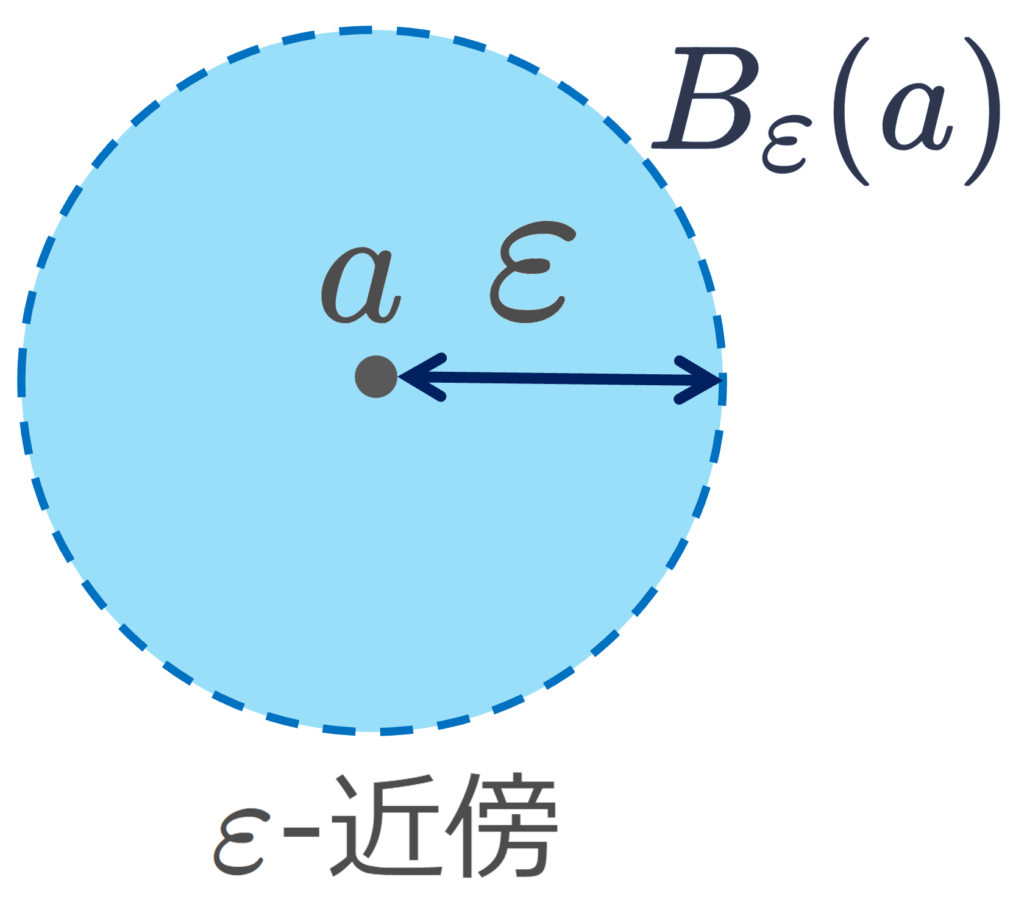
です。 \varepsilon >0 に対し,点 a\in \R^n における \varepsilon-近傍を
とします。すなわち,a\in \R^n と距離が \varepsilon 未満の点の集合です。
ユークリッド空間における開集合
まずは開集合を定義しましょう。
定義1(ユークリッド空間の開集合)
\R^n の部分集合 A\subset \R^n について,次の条件をみたすとき, A を開集合 (open set) という。
任意の x\in A に対し,ある \varepsilon>0 が存在して, B_\varepsilon (x)\subset A となる。
ただし,空集合 \emptyset も開集合と考える。
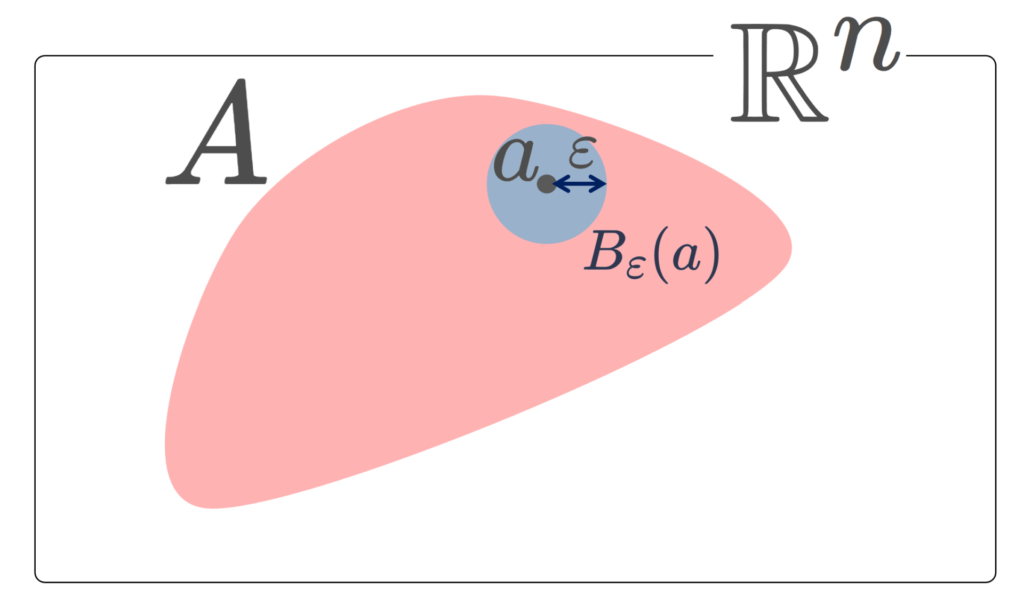
A 内のどんな点を取っても,その点の周りに A に入る円板が描けるような集合 A を開集合というわけです。具体例をみてイメージを膨らませましょう。
ユークリッド空間における開集合の例
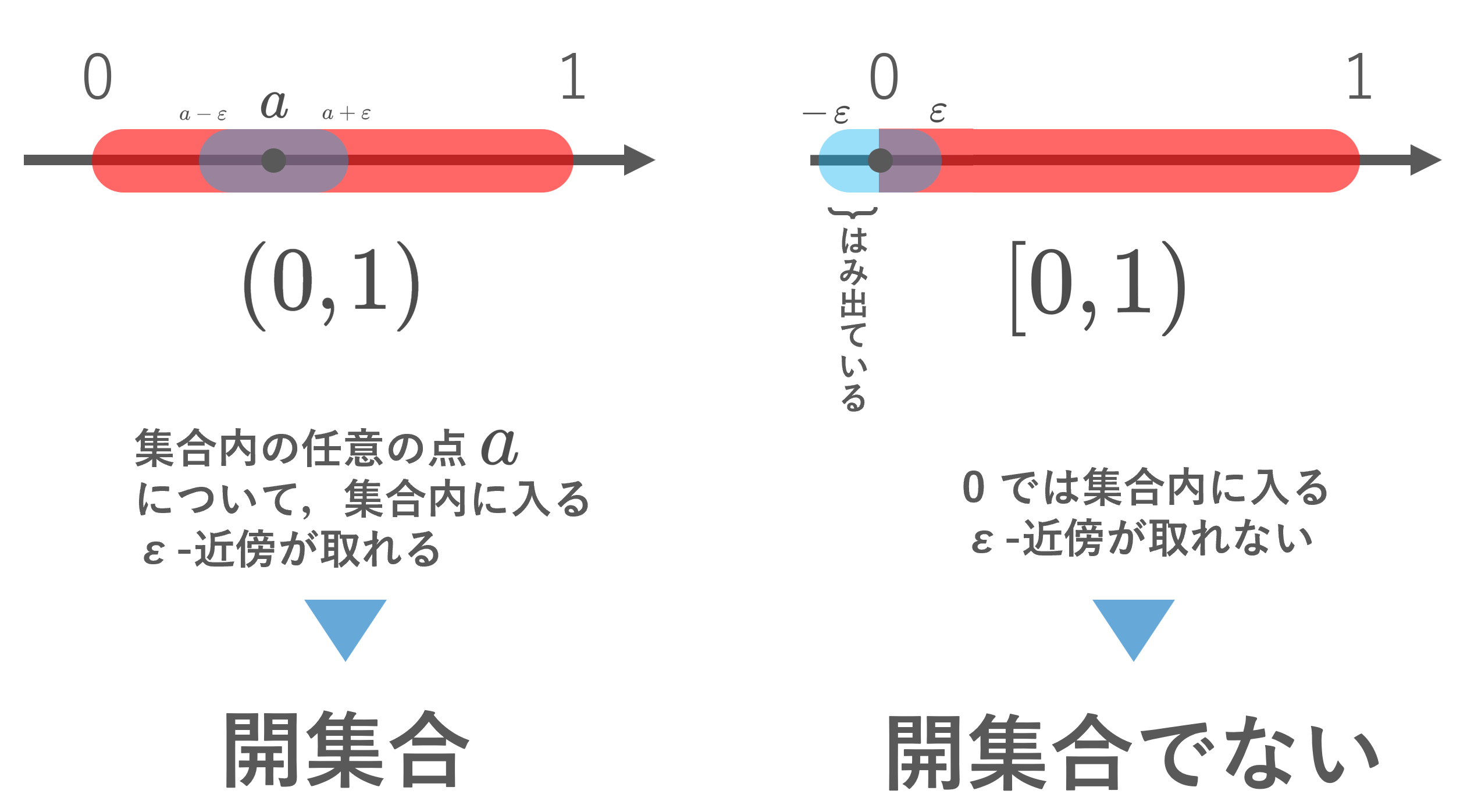
開集合の例1(\R における区間)
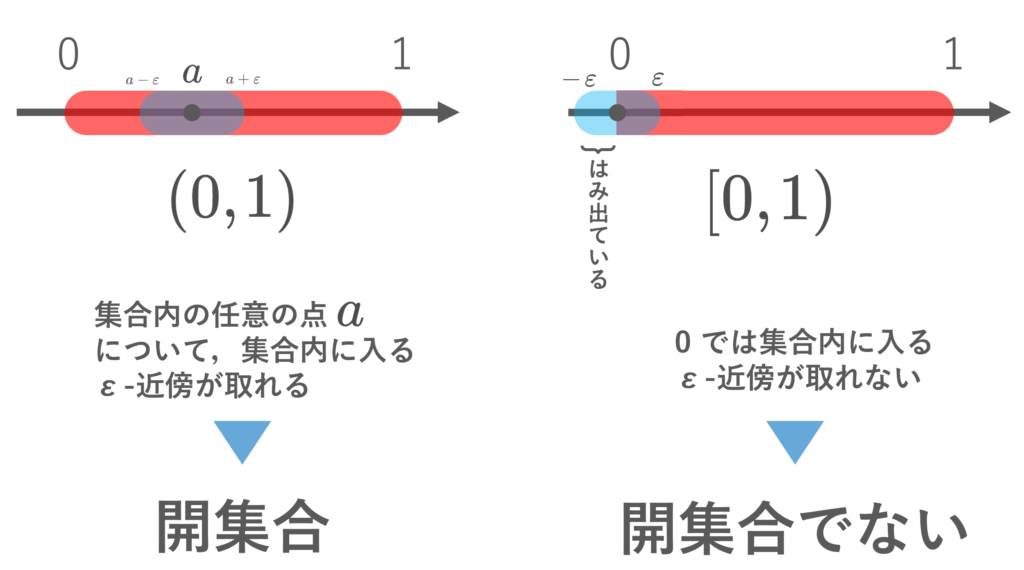
開区間 (0,1)\subset \R は開集合である。一方で, [0,1), (0,1], [0,1]\subset \R は開集合でない。
他に, (-\infty, 0), (0,\infty), (-\infty, \infty)=\R は開集合であるが, (-\infty, 0], [0,\infty), \{x\}\subset \R は開集合でない。
(0,1) だけでなく,より一般の (a,b) でも同じです。
任意の a\in (0,1) に対し, 0<\varepsilon < \min\{ a, 1-a\} となる \varepsilon をとると,
(a-\varepsilon , a+\varepsilon )\subset (0,1)
とでき, \R において左辺は B_\varepsilon(a) のことを指すので,開集合です。一方で, [0,1) における点 0 については, (-\varepsilon , \varepsilon )\subset [0,1) となる \varepsilon >0 は存在しないため,開集合ではありません。 (0,1],[0,1] も同様に開集合ではありません。
1点集合 \{x\} についても, (x-\varepsilon , x+\varepsilon )\subset \{x\} となる \varepsilon >0 は存在しませんので,開集合ではありません。一方で,全体集合 \R は,任意の a\in \R に対して,(a-1, a+1)\subset \R とできますから,開集合です。
開集合の例2(\Rにおける他の集合)
\R において, (0,1)\cup (2,3) や (-\infty, 0)\cup (0,\infty) は開集合である。
また,整数全体の集合 \mathbb{Z} や有理数全体の集合 \mathbb{Q} は開集合でない。
(0,1)\cup (2,3) のように,開区間を組み合わせたものも開集合です。
一方, q\in \mathbb{Q} に対し, (q-\varepsilon,q+\varepsilon)\subset \mathbb{Q} をみたす \varepsilon >0 は存在しませんから,\mathbb{Q} は 開集合ではありません。\mathbb{Z} も同じです。
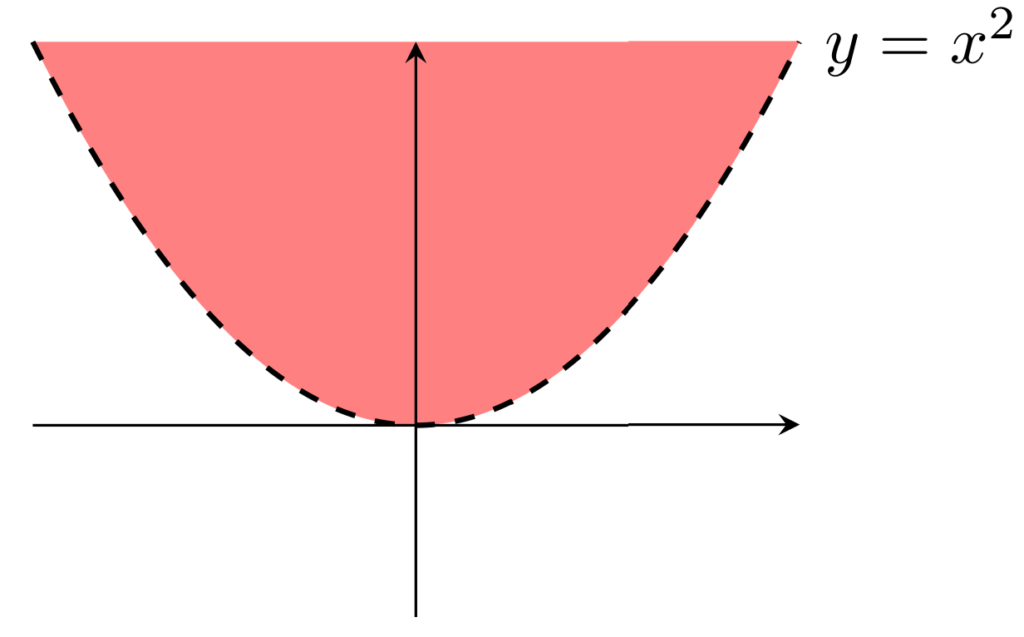
開集合の例3(\R^2)
\R^2 において,
A= \{(x, y)\in \R^2 \mid y>x^2\}
は開集合である。
ユークリッド空間における閉集合
つづいて,閉集合について考えます。
定義2(ユークリッド空間における閉集合)
\R^n の部分集合 A\subset \R^n について,次の条件をみたすとき A を閉集合 (closed set) という。
任意の収束する点列 \{x_n\} \subset A に対し, \lim_{n\to\infty}x_n\in A となる。
ただし,空集合 \emptyset も閉集合と考える。
A における点列が収束すれば,その収束先も A 内にあるということですね。一番イメージしやすい定義であると思いますが,その他の定義方法もあるので,後で紹介しましょう。
ユークリッド空間における閉集合の例
閉集合の例1(\R)
閉区間 [0,1]\subset \R は閉集合である。一方で, (0,1),[0,1), (0,1]\subset \R は閉集合でない。
他に, (-\infty, 0], [0,\infty), (-\infty, \infty)=\R, \{x\}\subset \R は閉集合であるが, (-\infty, 0), (0,\infty) は開集合でない。
[0,1] だけでなく,より一般の [a,b] でも同じです。
\{x_n\} \subset [0,1] が x\in \R に収束するとすると, x\in [0,1] です。よって, [0,1] は閉集合です。
一方で, \{x_n\} \subset (0,1) が x\in \R に収束するとしても, x\in (0,1) とは限りません。たとえば, x_n =1/n とすると, x=0 ですね。よって, (0,1) は閉集合ではありません。
また, \R の収束列は,実数値に収束するため, \R は閉集合であり,1点集合 \{x\} 上の点列は x,x,x,\ldots しかなく,これは x に収束するため, \{x\} は閉集合です。
閉集合の例2(\Rにおける他の集合)
\R において, [0,1]\cup [2,3] や整数全体の集合 \mathbb{Z} は閉集合である。
一方で有理数全体の集合 \mathbb{Q} は閉集合でない。
[0,1]\cup [2,3] のように,閉区間の和集合も閉集合です。また, \mathbb{Z} における数列が収束するには,最終的にずっと同じ整数になっていないといけないため,その整数が収束値であり, \mathbb{Z} は閉集合だと分かります。
一方で,有理数列は,収束しても必ずしも収束先が有理数になるといえませんから,\mathbb{Q} は閉集合ではありません。
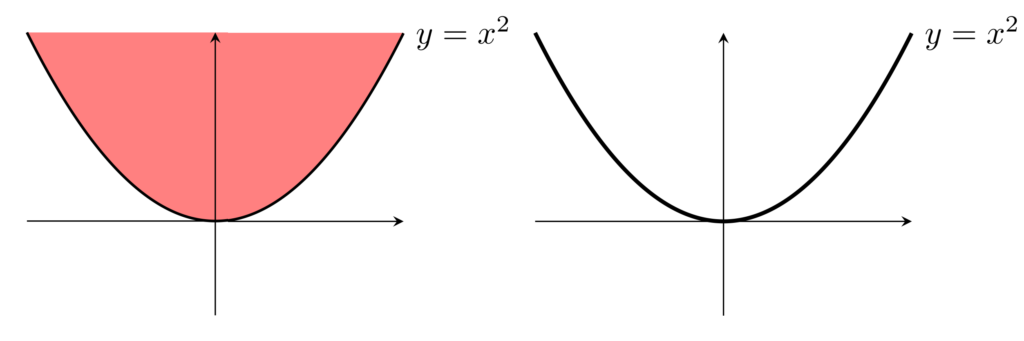
閉集合の例3(\R^2)
\R^2 において,
A= \{(x, y)\in \R^2 \mid y\ge x^2\}
は閉集合である。また,
も閉集合である。
ここで,注意を述べておきます。
ユークリッド空間の内部(開核)・境界・外部と開集合・閉集合
ユークリッド空間の内部(開核)・境界・外部と,開集合・閉集合の関係について述べましょう。
まず,集合における内部(開核)・境界・外部について,定義を紹介しましょう。詳しくは,内部(開核)・外部・境界について詳しく図解~距離空間・位相空間~で解説しています。
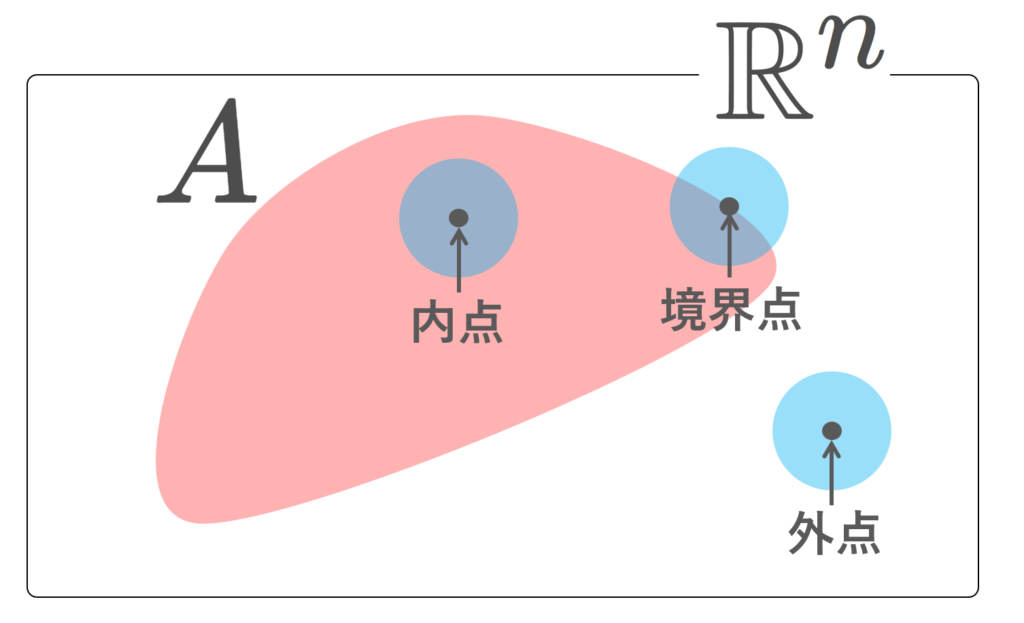
A\subset \R^n とする。
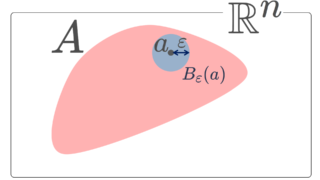
- a\in \R^n とする。ある \varepsilon >0 が存在して,
\color{red}B_\varepsilon(a)\subset A
とできるとき,a を A の内点 (interior point) という。 A の内点全体の集合を A の内部 (interior) または開核といい, A^\circ または A^i または \color{red} \operatorname{Int}(A) とかく。 - A^c の内点を A の外点 (exterior point) という。 A の外点全体の集合(すなわち A^c の内部)を A の外部 (exterior point) といい,A^e または \color{red} \operatorname{Ext}(A) とかく。外点は,ある \varepsilon>0 が存在して,
\color{red}B_\varepsilon(a)\cap A=\emptyset
とできる点 a\in \R^n,と定義してもよい。 - A の内点でも外点でもない集合を A の境界点 (boundary point) という。 A の境界点全体の集合を境界 (frontier, boundary) といい, A^f または \color{red} \partial A とかく。境界点は,任意の \varepsilon >0 に対し,
\color{red}B_\varepsilon(a)\cap A\ne \emptyset\,\text{ and }\, B_\varepsilon(a)\cap A^c\ne \emptyset
となる点 a\in \R^n,と定義してもよい。
以下の図がイメージしやすいでしょう。
詳しくは,以下で解説しています。
内部(開核)・境界・外部を知っていると,開集合・閉集合は以下のように定義してもかまいません。
定義3(開集合・閉集合の内部(開核)・境界・外部を用いた定義)
\R^n の部分集合 A\subset \R^n について,
- \large\color{red}A= \operatorname{Int}(A) をみたすとき, A を開集合 (open set) という。
- \large \color{red}A = \operatorname{Int}(A)\cup \partial A をみたすとき, A を閉集合 (closed set) という。これは,「任意の \varepsilon >0 に対し,
\large B_\varepsilon (a)\cap A\ne \emptyset
となる点 a\in \R^n 全体が A に一致する集合 A」を閉集合と言っても同じである。
定義1,2との同値性を軽く確認しておきましょう。
定義1, 2と3の同値性の証明
開集合については,定義を少し言い換えたに過ぎないから明らか。
閉集合について示す。 A\subset \R^n が定義3.2の意味で閉集合であるとする。 \{ a_n\}\subset A を任意の収束列とする。収束先を a\in \R^n とすると,任意の \varepsilon >0 に対し,ある N\ge 1 が存在して,
n\ge N \implies d(a_n, a)<2\varepsilon
とできる。これにより, a_n\in B_\varepsilon (a) \cap A\; (n\ge N) となるため, B_\varepsilon (a) \cap A\ne\emptyset である。 A は定義3.2の意味で閉集合なので, a\in A でなければならず,これにより, A は定義2の意味で閉集合である。
逆に, A\subset \R^n が定義2の意味で閉集合であるとする。 a\in \R^n が任意の \varepsilon >0 で B_\varepsilon (a)\cap A\ne \emptyset をみたすとする。各 n\ge 1 に対し, a_n \in B_{1/n} (a)\cap A となる点を取り,数列 \{a_n\} を構成すると, a_n \xrightarrow{n\to\infty} a である。定義2より, a\in A である。ゆえ, A は定義3.2もみたしている。
証明終
距離空間における開集合・閉集合
距離空間における開集合・閉集合の定義は,ユークリッド空間におけるものと全く同じと考えて問題ないです。
以下で, (X, d) を距離空間とします。 \varepsilon >0 に対し,点 a\in X における \varepsilon-近傍を
\textcolor{red}{\large B_\varepsilon(a)}=\{ x\in X \mid d(a, x)<\varepsilon\}
とすると,定義は全く同じです。
定義4(距離空間における開集合・閉集合)
(X, d) を距離空間とし, A\subset X とする。
- 任意の x\in A に対し,ある \varepsilon>0 が存在して, B_\varepsilon (x)\subset A となるとき, A を開集合 (open set) という。ただし,\emptyset も開集合と考える。
- 任意の収束する点列 \{x_n\} \subset A に対し, \lim_{n\to\infty}x_n\in A となるとき, A を閉集合 (closed set) という。ただし,\emptyset も閉集合と考える。
集合の内部(開核)・境界・外部を使って,別の定義ができることもユークリッド空間のときと同じなので省略します。
距離空間における開集合・閉集合の例
(X, d) を離散距離空間とする。すなわち,
d(x,y)=\begin{cases} 0 & x=y, \\ 1 & x \ne y\end{cases}
とする。このとき,すべての部分集合が開集合かつ閉集合である。
A\subset X とすると,a\in A に対し,
\{a\} = B_{1/2}(a)\subset A
ですから, A は開集合です。また, A の点列が収束するなら,いずれは a,a,a,a,\ldots となるはずで, a\in A なので閉集合です。
ユークリッド空間・距離空間における開集合・閉集合の性質
開集合・閉集合における大事な性質を紹介し,証明しておきましょう。
1. 開集合・閉集合の補集合
定理1(開集合・閉集合の補集合)
開集合の補集合は必ず閉集合である。逆に,閉集合の補集合は必ず開集合である。
証明
(X, d) を距離空間とし, A\subset X を開集合とすると,内部(開核)・外部・境界について詳しく図解~距離空間・位相空間~より, X は3つの非交和
X=\operatorname{Int}(A)\cup \partial A \cup \operatorname{Ext}(A)
と分解できる。 A は開集合なので, \operatorname{Int}(A)=A であり,
となるから, A^c は閉集合である。ただし,上式の最後の等号は内部(開核)・外部・境界について詳しく図解~距離空間・位相空間~にかいてある。
証明終
2. 開集合系のみたす性質
定理2(開集合系)
(X, d) を距離空間とし, \mathcal{O}\subset 2^X ( 2^X はべき集合)を X における開集合全体の集合とする。このとき,以下が成立する。
- \emptyset\in \mathcal{O},\, X\in \mathcal{O}.
- O_1, O_2, \ldots, O_n \in \mathcal{O} のとき, \bigcap_{k=1}^n O_k \in \mathcal{O}.
- \{O_\lambda\}_{\lambda\in \Lambda} \subset \mathcal{O} とするとき, \bigcup_{\lambda\in \Lambda} O_\lambda \in\mathcal{O}.
2.は有限個の共通部分,3.は無限個,もっと言えば非可算無限個でも構いません。
「急に何だ」と思ったかもしれませんが,実は位相空間の定義をするにあたって,この3つの性質は非常に重要です。この3つの性質に着目して位相空間の定義に一般化されるからです。証明しておきましょう。
証明
1.について
\emptyset\in \mathcal{O} は定義より直ちにわかる。 X\in \mathcal{O} については,任意の x\in X に対し, B_1(x)\subset X よりわかる。
2.について
x\in O_1\cap O_2\cap \cdots\cap O_n とする。 1\le k\le n に対し, x\in O_k より, \varepsilon_k >0 が存在して, B_{\varepsilon_k} (x)\subset O_k とできる。
\varepsilon =\min\{ \varepsilon_1,\varepsilon_2, \ldots, \varepsilon_n\}
とすると,すべての 1\le k\le n で B_{\varepsilon} (x)\subset O_k となるから,
となる。したがって,O_1\cap O_2\cap \cdots \cap O_n\in \mathcal{O} である。
3.について
x\in \bigcup_{\lambda\in \Lambda} O_\lambda とすると,ある \lambda\in \Lambda が存在して, x\in O_\lambda となる。 O_\lambda\in\mathcal{O} なので,ある \varepsilon >0 が存在して,
B_\varepsilon (x)\subset O_\lambda\subset \bigcup_{\lambda\in \Lambda} O_\lambda
となるから, \bigcup_{\lambda\in \Lambda} O_\lambda\in \mathcal{O} である。
証明終
注意ですが,2.を無限個にすることはできません。たとえば, \R^n において,各 n\ge 1 で B_{1/n}(a) は開集合ですが, \bigcap_{n=1}^\infty B_{1/n}(a) =\{a\} であり,1点集合 \{a\} は開集合ではありません。
より一般の位相空間における開集合・閉集合
上の定理2を一般化したものが,位相空間です。位相空間についても,開集合・閉集合の概念がありますが,定理2で開集合を定義し,定理1で閉集合を定義することが最もメジャーです。位相空間における開集合・閉集合は以下で解説しています。