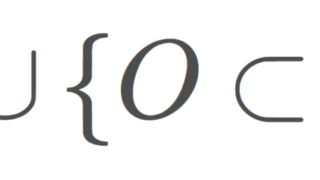位相空間論におけるコルモゴロフ空間,あるいは T_0 空間とは, T_0-分離公理と呼ばれるものを満たす空間です。分離公理 (separation axioms) とは,各点が位相的にどのくらい「離れている」かを測る指標です。
コルモゴロフ空間について,その定義と具体例をフレシェ空間( T_1 空間)やハウスドルフ空間( T_2 空間)を織り交ぜながら,掘り下げましょう。
コルモゴロフ空間(T0空間)の定義と同値な性質
定義(コルモゴロフ空間・ T_0 空間)
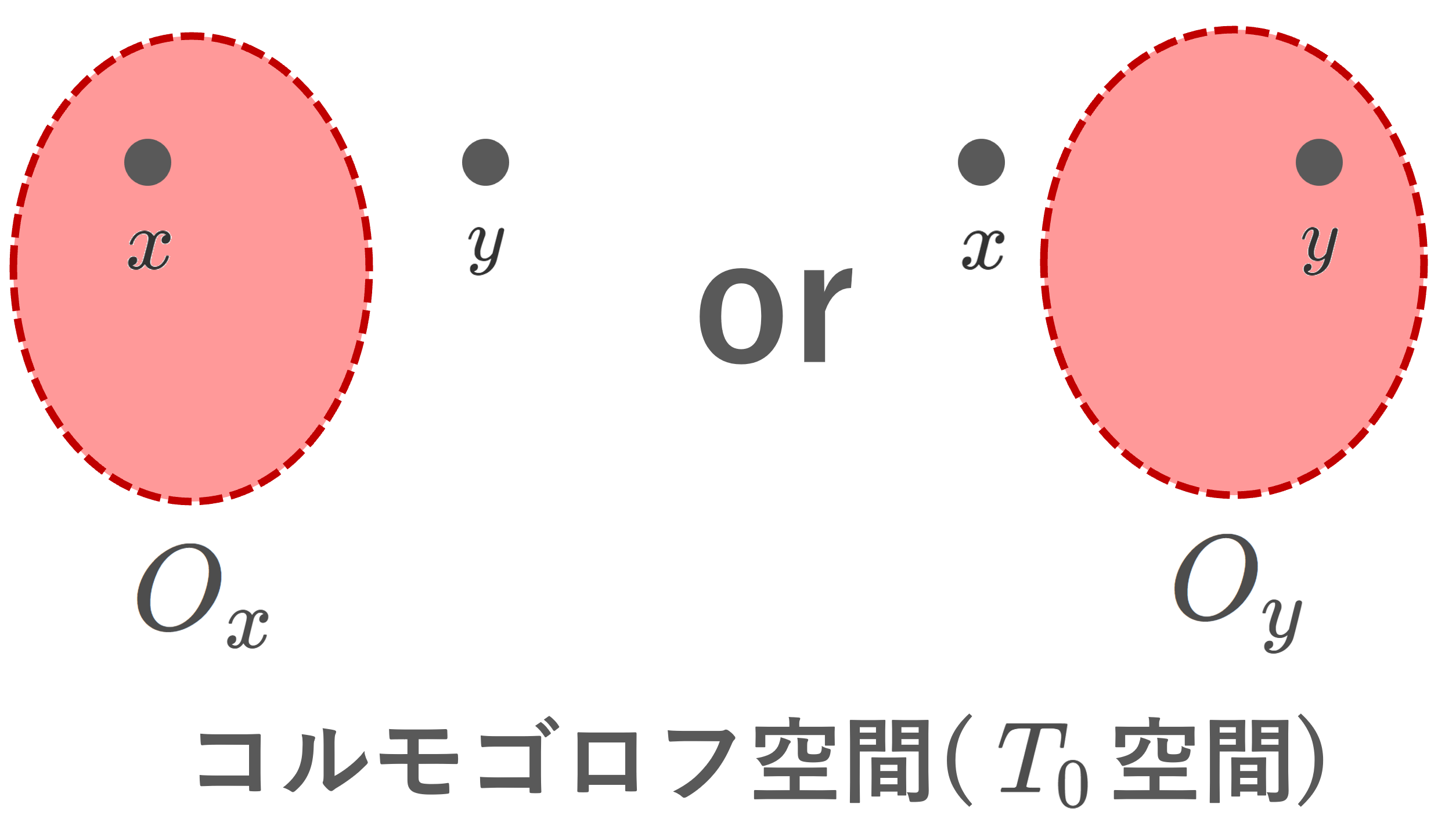
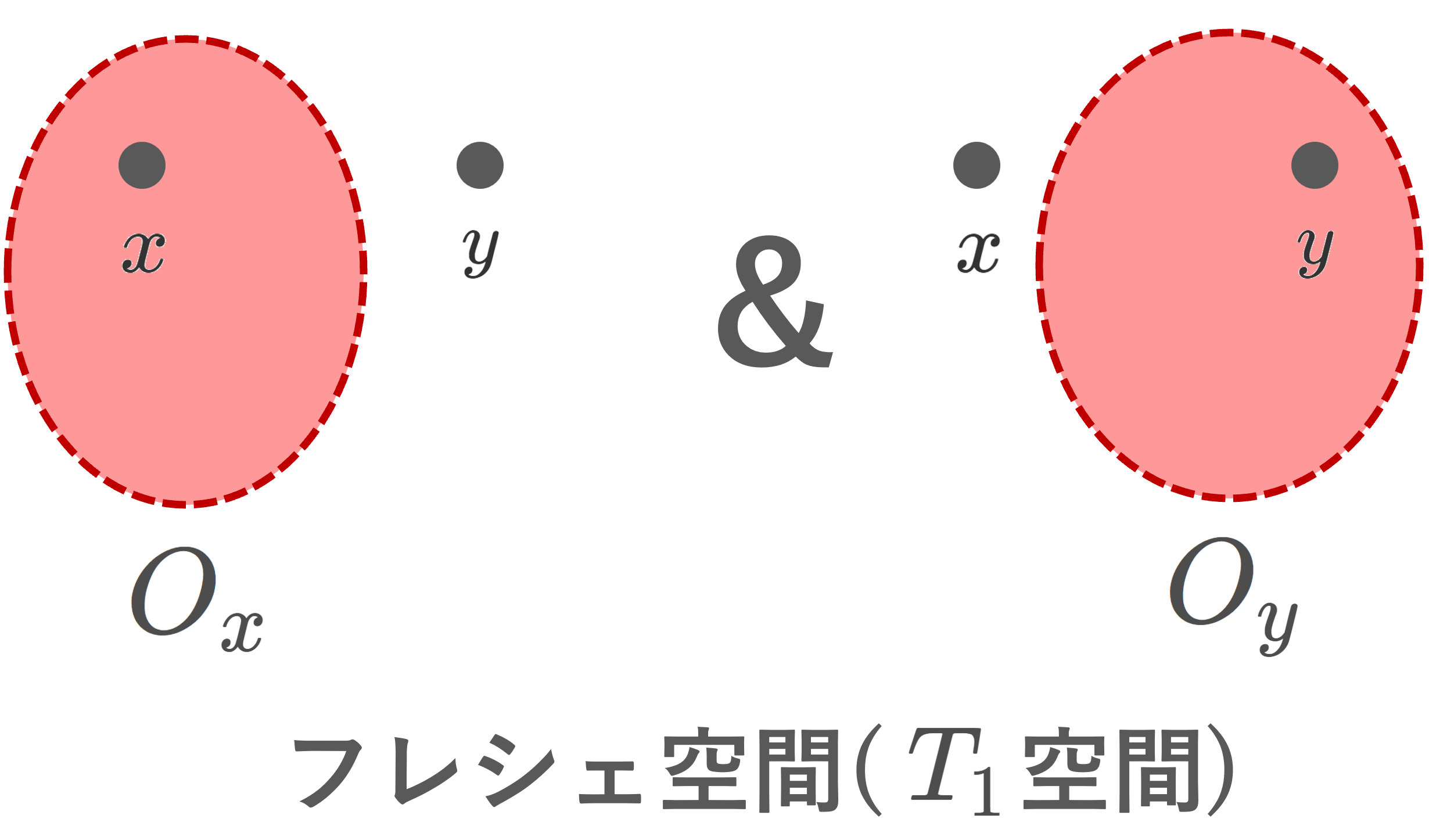
(X,\mathcal{O}) を位相空間とする。任意の異なる点 x, y\in X に対し,
x\in O_x かつ y \notin O_x となる O_x\in\mathcal{O}
x\notin O_y かつ y \in O_y となる O_y\in\mathcal{O}
のうち,少なくとも一方が存在するとき, (X,\mathcal{O}) はコルモゴロフ空間 (Kolmogorov space) または T_0 空間 ( T_0 space) という。

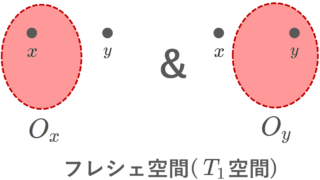
「少なくとも一方」ではなく, O_x, O_y のどちらも存在するときはフレシェ空間 (Fréchet space) または T_1 空間 ( T_1 space) といいます(→【位相空間】T1空間の定義・具体例と性質)。定義より, \color{red} T_1\implies T_0 です。なお,フレシェ空間という言葉は,関数解析学の文脈では別の意味で使われることがあるため,注意が必要です。
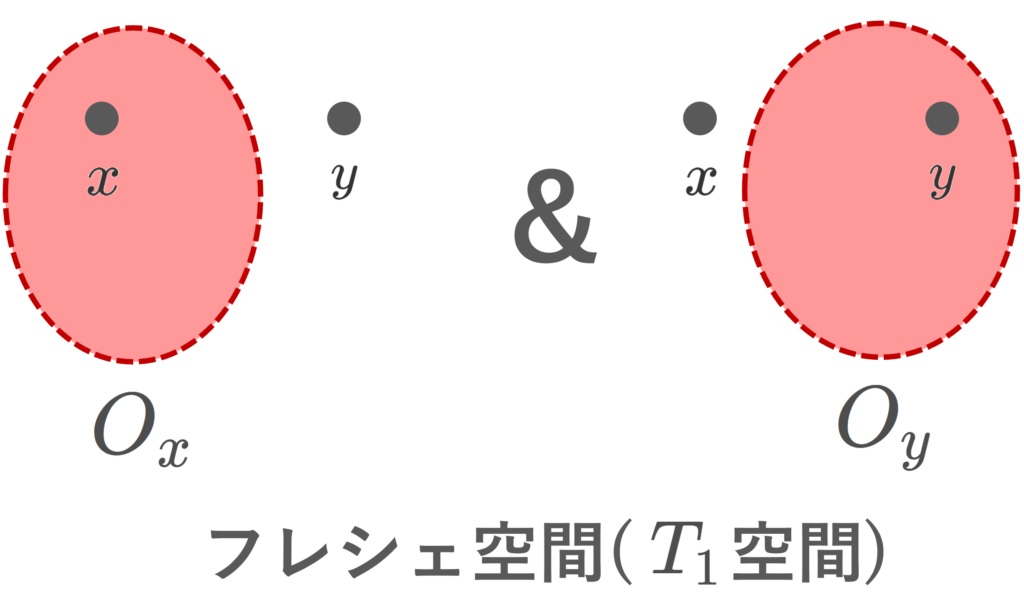
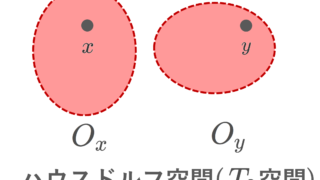
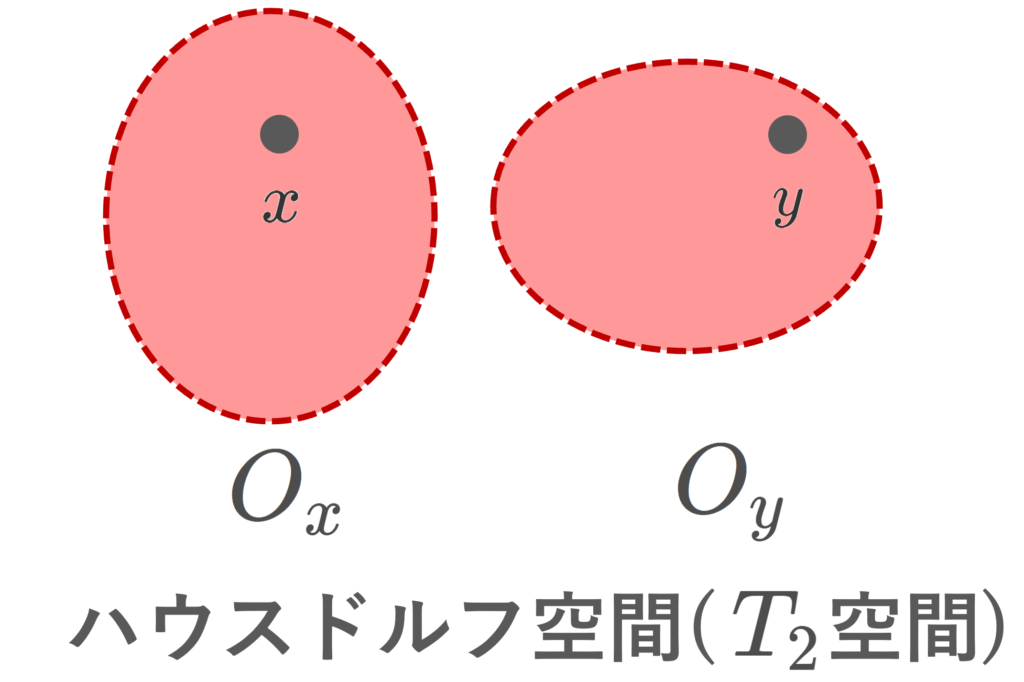
また,さらに,フレシェ空間( T_1 空間)であって,かつ常に O_x\cap O_y =\emptyset となるような O_x, O_y が取れるとき,ハウスドルフ空間 (Hausdorff space) または T_2 空間 ( T_2 space) といいます(→ハウスドルフ空間(T2空間)の定義・具体例・性質を詳しく)。定義より, \color{red} T_2\implies T_1\implies T_0 です。
コルモゴロフ空間( T_0 空間)でない空間を考えましょう。この空間では,ある異なる2点 x,y\in X が存在して,任意の開集合 O\in\mathcal{O} に対し, x\in O\iff y\in O が成り立つことになります。これは,開集合によって点が分離できない空間といえます。空間上の点が,位相的に識別不可能 (topologically indistinguishable) ということもあります。
逆に,コルモゴロフ空間( T_0 空間)は,各点が位相的に識別可能 (topologically distinguishable) といいます。
コルモゴロフ空間( T_0 空間)と同値な性質を紹介します。
定理1(コルモゴロフ空間( T_0 空間)の同値な性質)
(X,\mathcal{O}) を2点以上の点を持つ位相空間とするとき,以下は同値である。
位相空間は「近傍」の概念により,「近さ」の議論ができますが,2つ目が成り立てば,任意の2点の位相的な「近さ」が異なるといっています。これは,位相的に識別可能なことと対応しています。
証明
1. \implies 2.について
x, y\in X を異なる2点とする。X はコルモゴロフ空間( T_0 空間)なので,ある開集合 O_x\in\mathcal{O} が存在して, x\in O_x,\, y\notin O_x としても一般性を失わない。
このとき, O_x\in\mathcal{N}(x) だが, O_x\notin \mathcal{N}(y) なので,\mathcal{N}(x)\ne\mathcal{N}(y) である。
2.\implies 1.について
x, y\in X を異なる2点とする。近傍系は空集合ではないので,\mathcal{N}(x)\ne\mathcal{N}(y) ならば, N_x\in \mathcal{N}(x)\setminus \mathcal{N}(y) が存在するか,または N_y\in \mathcal{N}(y)\setminus \mathcal{N}(x) が存在する。前者と思ってよい。
このとき,ある開集合 O_x\in\mathcal{O} が存在して, x\in O_x\subset N_x とできる。 y\notin O_x である(もし y\in O_x なら N_x\in\mathcal{N}(y) となってしまう)から,コルモゴロフ空間( T_0 空間)である。
証明終
コルモゴロフ空間(T0空間)とそうでない例
具体例を見ていきましょう。フレシェ空間( T_1 空間)やハウスドルフ空間( T_2 空間)も絡めて見ていきます。
例1(密着空間・離散空間).
X を2元以上の集合とする。
(X, \{\emptyset, X\}) を密着空間とするとき,これは T_0 でも T_1 でも T_2 でもない。
(X, 2^X) を離散空間とするとき,これは T_0, T_1, T_2 である。
密着空間は開集合によって点が分離できず,離散空間は1点集合自身が開集合であるため,全ての点が開集合によって分離できます。
例2( \R).
実数の集合 \R に通常の位相を入れた空間はハウスドルフ空間( T_2 空間)であるため, T_1, T_0 でもある。
T_2\implies T_1\implies T_0 なので言えますね。
例3(距離空間).
距離空間はハウスドルフ空間( T_2 空間)であるため, T_1, T_0 でもある。
もっといろいろな例を挙げましょう。
例4.
X=\{a,b,c\},\,\mathcal{O}=\{\emptyset, \{a\}, \{a,b\} ,X \} とすると,(X,\mathcal{O}) は位相空間である。
この空間は, T_0 であるが T_1 ではない。
a と b は, a\in\{a\},\, b\notin \{a\} とできる, a と c は, a\in\{a\},\, c\notin \{a\} とできる, b と c は, b\in\{a,b\},\,c\notin \{a,b\} とできるので, T_0 です。
一方で, a\notin O,\, b\in O となる O\in \mathcal{O} はないので, T_1 ではありません。
例5(特定点位相).
X を2元以上の集合とし, x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\in O\}\cup\{\emptyset\}
とすると, (X,\mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
x を元に持つ集合全体(と \emptyset )を開集合族とする位相空間です。たとえば, x\ne a とすると, x\in \{x\},\,a\notin \{x\} だし, a\ne b をともに x と異なるとすると, a\in \{x,a\},\, b\notin \{x,a\} とできるので, T_0 です。
一方で, x\ne a に対し, x\notin O,\, a\in O となる O\in\mathcal{O} は存在しないので, T_1 ではありません。
特定点位相については,以下で掘り下げています。
例6(除外点位相).
X を2元以上の集合とし, x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\notin O\}\cup\{X\}
とすると, (X,\mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
さっきと逆で, x を元に持たない集合全体(と X)を開集合族とする位相空間です。 T_0 であることは確認してみてください。 x\ne a に対し, x\in O,\, a\notin O となる O\in\mathcal{O} は存在しないので, T_1 ではありません。
除外点位相は以下でも解説しています。
例7.
\mathcal{O}=\{ (0, x)\mid 0<x\le 1\}\cup\{\emptyset\}
とすると, ((0,1), \mathcal{O}) は位相空間である。この空間は T_0 であるが, T_1 ではない。
0<x<y\le 1 に対し, x\in O,\, y\notin O となる O\in\mathcal{O} は存在しますが,逆に x\notin O,\, y\in O となる O\in\mathcal{O} は存在しませんね。
例8( p 乗可積分空間).
f\colon \R\to \mathbb{C} を 1\le p<\infty 乗可積分関数,すなわち可測でかつ \int_\R | f(x)|^p \, dx<\inftyとする。p 乗可積分関数全体の集合を \mathcal{L}^p とすると, f,g\in\mathcal{L}^p に対し,
\| f-g\|=\left(\int_\R |f(x)-g(x)|^p \, dx\right)^{1/p}
により, \mathcal{L}^p はセミノルム空間(したがって擬距離空間)になる。この空間は T_0 でない。
ただし, f=g, \, \text{a.e.} による同値関係によって同一視した商空間 L^p は, \|\cdot \| がノルムになる(したがって L^p は距離空間になる)ので, T_0,T_1, T_2 である。
\mathcal{L}^p においては, f=g, \, \text{a.e.} となる2つの関数 f,g\in\mathcal{L}^p が位相的に識別不可能なので, T_0 ではありません。(a.e.の意味はほとんどいたるところ(almost everywhere, a.e.)の議論を参照)
一般に,ノルム空間から \| x\| = 0\implies x=0 を除いたセミノルム空間や,距離空間の定義から d(x,y)=0\implies x=y を除いた擬距離空間は, T_0 にはなりません。
コルモゴロフ空間(T0空間)の性質
ある位相空間が T_0, T_1, T_2 なら,その部分空間も T_0, T_1, T_2 だし,直積空間もそうです。
定理2(分離公理と部分空間・直積)
1.については, T_2 の場合に,相対位相と部分位相空間の定義・具体例5つ・性質5つの中で証明しています。2.も T_2 の場合に直積位相とは~定義・具体例・性質~の中で証明しています。
その他の分離公理
それ以外の分離公理もまとめておきます。定義は文献[1]に依っています。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ | 任意の異なる2点 x,y\in X が開集合で分離される, すなわち x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_{2 \frac {1}{2}} 完全ハウスドルフ | 任意の異なる2点 x,y\in X が閉近傍で分離される, すなわち x\in O_x, \, y\in O_y,\, \overline{O_x}\cap \overline{O_y}=\emptyset となる開集合 O_x, O_y が取れる |
| ウリゾーン | 任意の異なる2点 x,y\in X が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f(x)=0,\, f(y)=1 となるものが取れる ※ ウリゾーンと T_{2\frac{1}{2}}(完全ハウスドルフ)の定義を逆にすることがある |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F が開集合で分離される, すなわち F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| 正則 (regular) | T_0 かつ T_3( \iff T_2 かつ T_3) ※ 正則と T_3 の定義を逆にすることがある |
| T_{3 \frac{1}{2}} 完全正則・チコノフ | 任意の閉集合 F と任意の点 x\in X\setminus F が連続関数で分離される, すなわち連続関数 f\colon X\to [0,1] で, f|_F=0,\, f(x)=1 となるものが取れる |
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| perfectly T_4 | T_4 かつ任意の閉集合が G_\delta 集合である |
| 正規 (normal) | T_1 かつ T_4( \iff T_2 かつ T_4\iff T_3 かつ T_4) ※ 正規と T_4 の定義を逆にすることがある |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの集合 A,B\subset X が開集合で分離される, すなわち A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
| completely 正規 | T_1 かつ T_5( \iff T_2 かつ T_5\iff T_3 かつ T_5) ※ completely 正規と T_5 の定義を逆にすることがある |
| T_6 perfectly 正規 | T_1 かつperfectly T_4 |