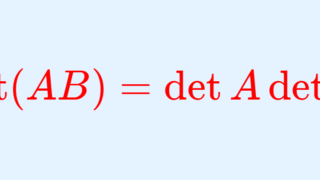行列の行基本変形・列基本変形について,定義と基本行列との演算対応,行列式との関係について順に解説します。
行基本変形とは
まずは行に関する基本変形を考えましょう。
定義(行基本変形)
m \times n 行列に対し,
- ある行の \boldsymbol{c} 倍を他の行に加えること
- 2つの行を入れ替えること
- ある行を \boldsymbol{ c \ne 0 } 倍すること
を行基本変形という。
3.は c\ne 0 であることに注意してください。
行基本変形を図で描いてみましょう。
ある行の c 倍を他の行に加える
第 i 行の c 倍を第 j 行に加えると以下のようになります。

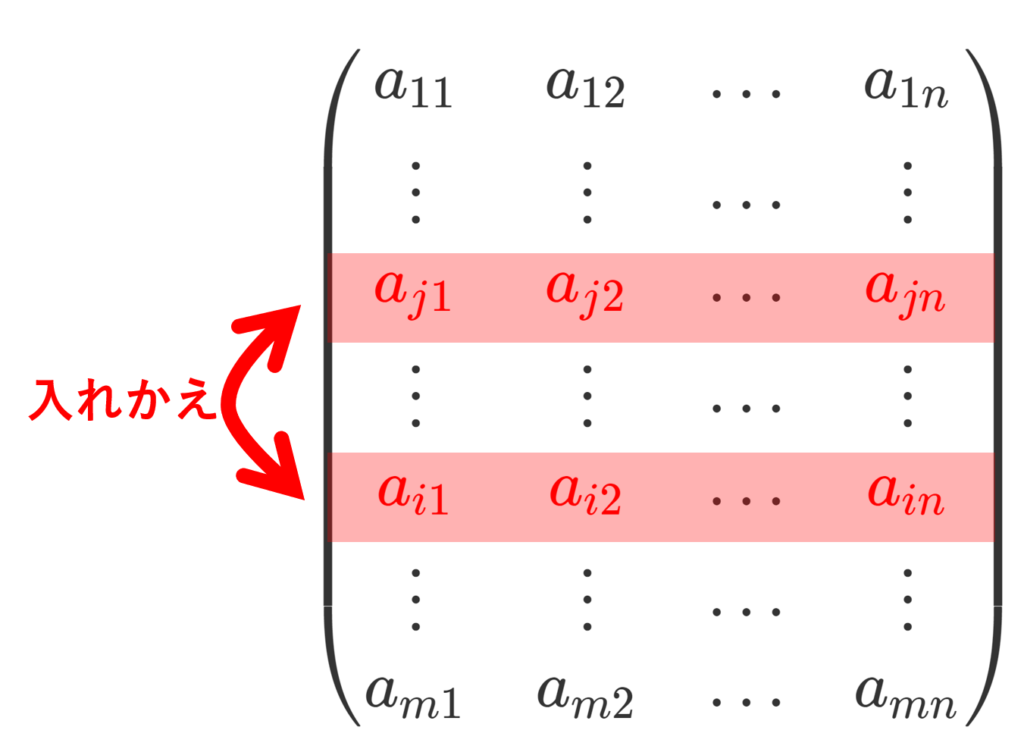
2つの行を入れ替える
第 i 行と第 j 行を入れ替えると以下のようになります。
ある行を c ≠ 0 倍すること
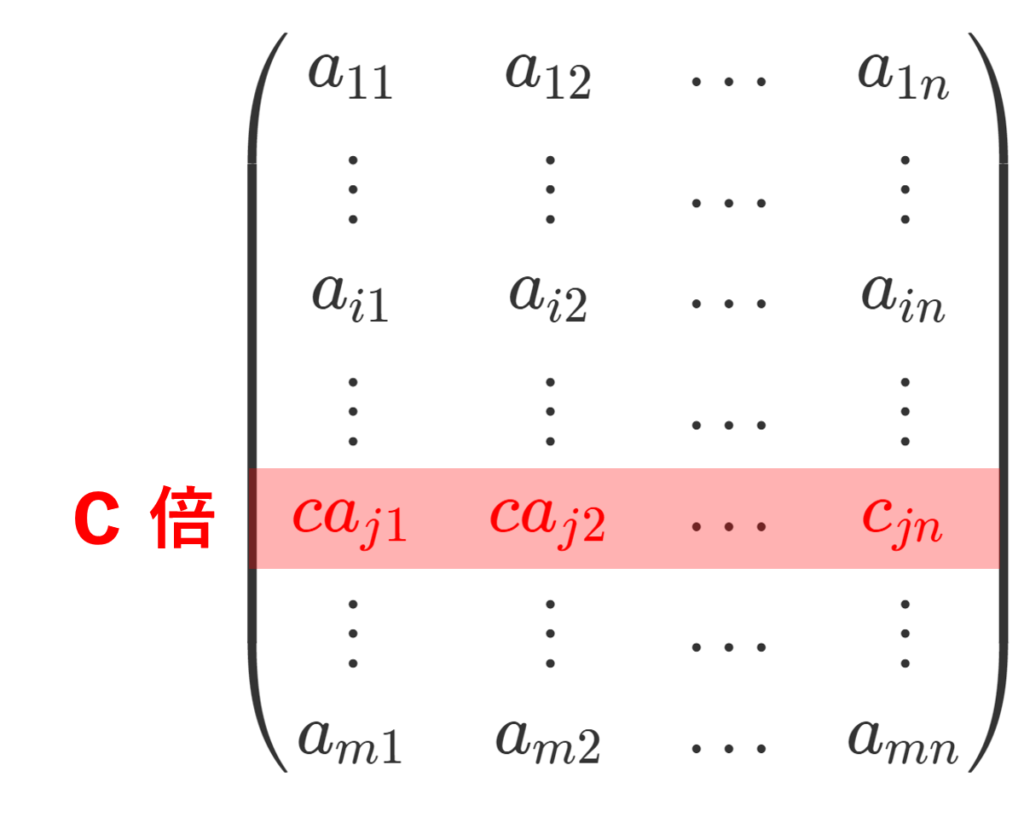
第 j 行を c \ne 0 倍すると以下のようになります。
列基本変形とは
次に,列基本変形について考えましょう。これは,行に関する基本変形をそのまま列に変えて適用したものになります。
定義(列基本変形)
m \times n 行列に対し,
- ある列の \boldsymbol{c} 倍を他の列に加えること
- 2つの列を入れ替えること
- ある列を \boldsymbol{ c \ne 0 } 倍すること
を列基本変形という。
列基本変形を図で描いてみましょう。
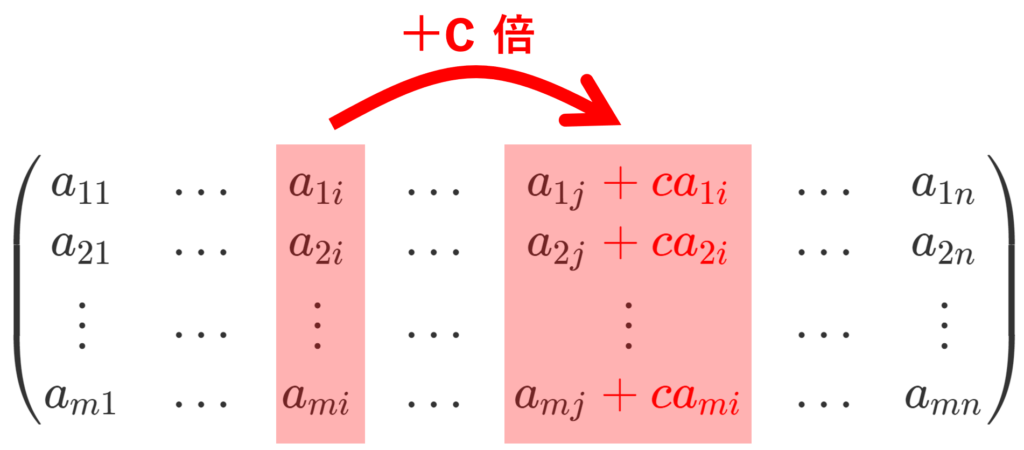
ある列の c 倍を他の列に加える
第 i 列の c 倍を第 j 列に加えると以下のようになります。
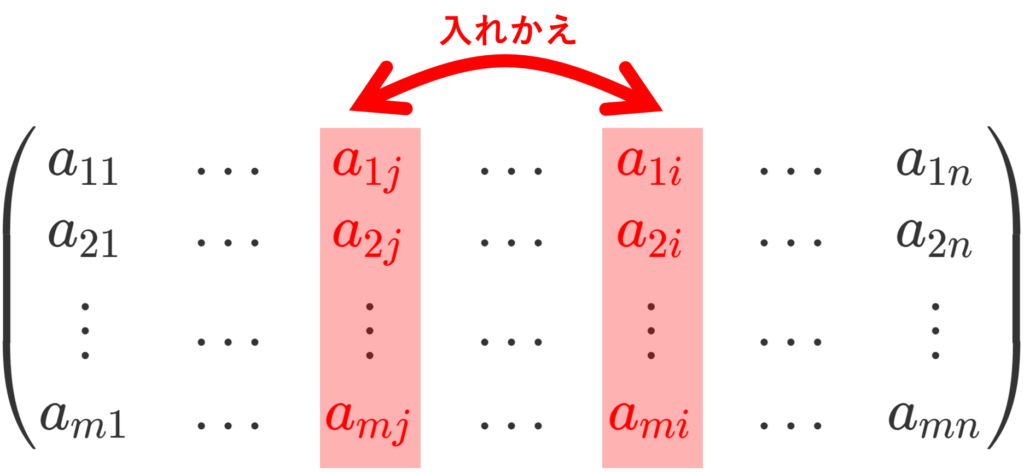
2つの列を入れ替える
第 i 列と第 j 列を入れ替えると以下のようになります。
ある列を c ≠ 0 倍すること
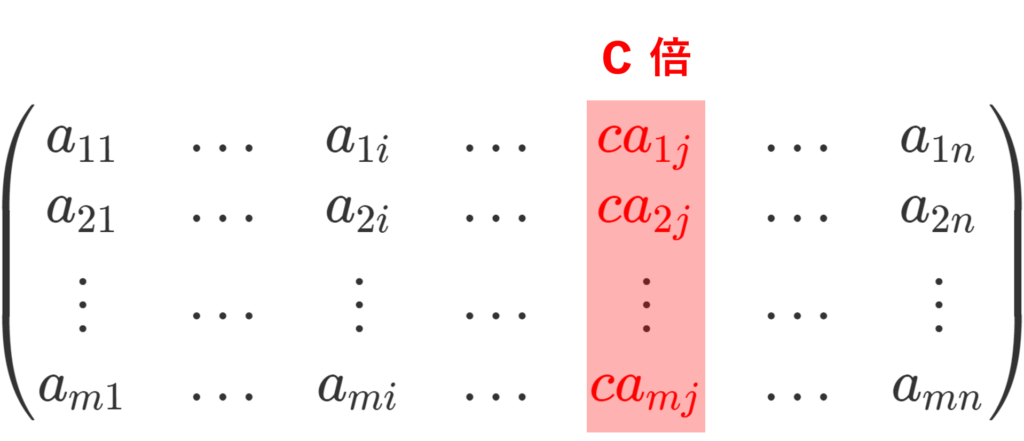
第 j 列を c \ne 0 倍すると以下のようになります。
基本変形の演算対応と基本行列
基本変形は,以下のような演算に対応させることができます。
定理(基本変形と演算対応)
m \times n 行列に対し,
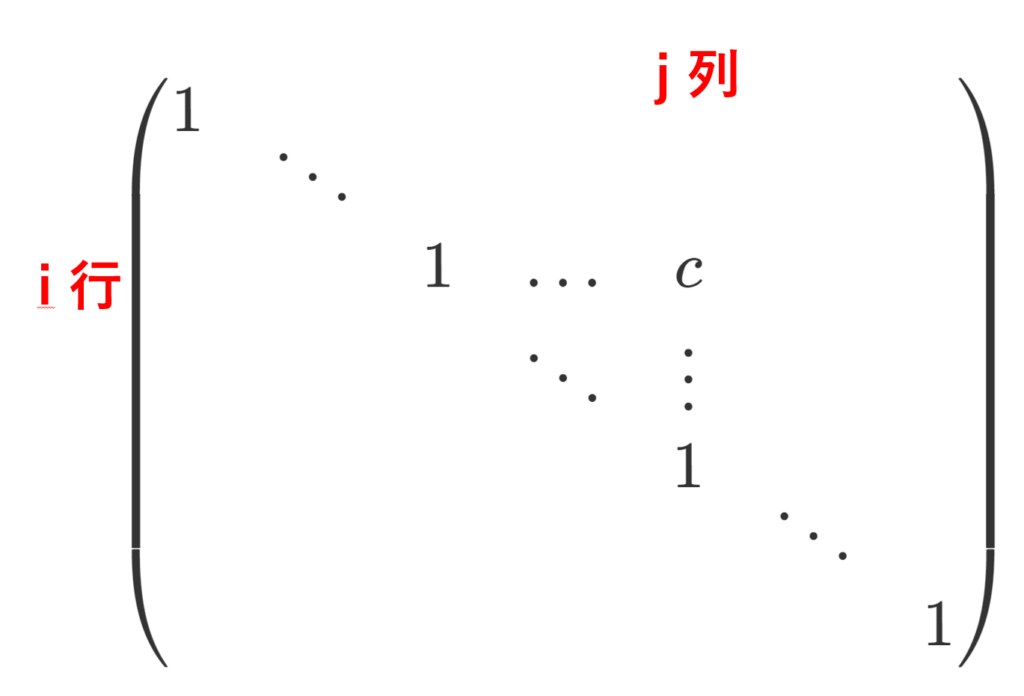
1. 第 \color{red} j 行(第 i 列)の c 倍を第 \color{red}i 行(第 j 列)に加える変形は,以下の m 次( n 次)正方行列を左(右)からかけることと同じである。
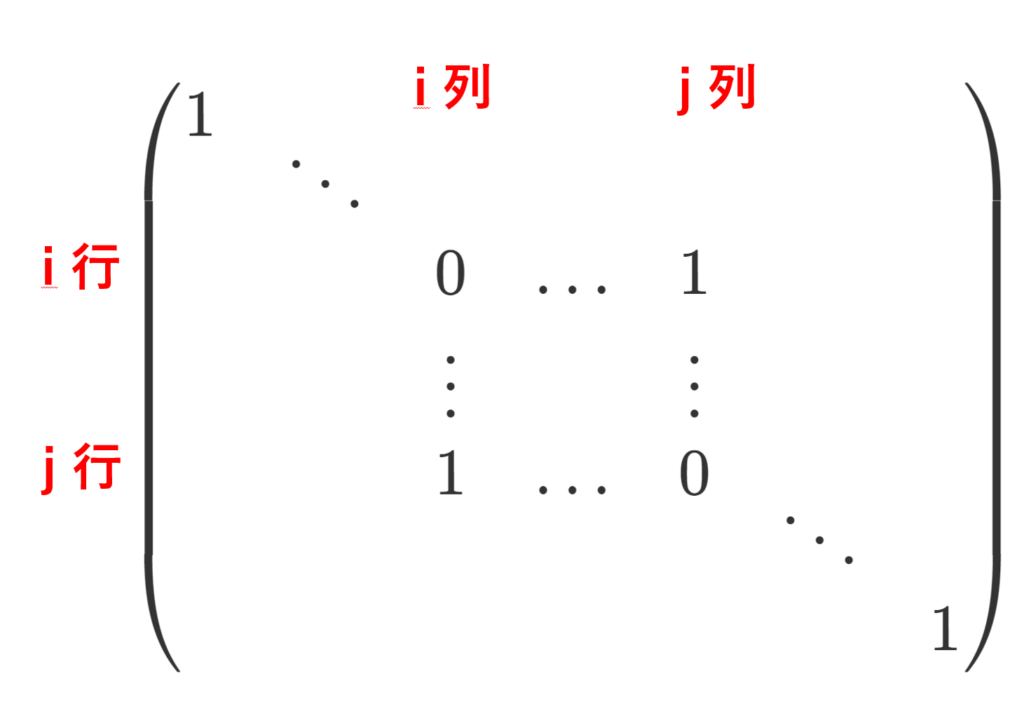
2. 第 i 行(列)と第 j 行(列)を入れ替える変形は,以下の m 次( n 次)正方行列を左(右)からかけることと同じである。
3. 第 j 行(列)を c \ne 0 倍する変形は,以下の m 次( n 次)正方行列を左(右)からかけることと同じである。
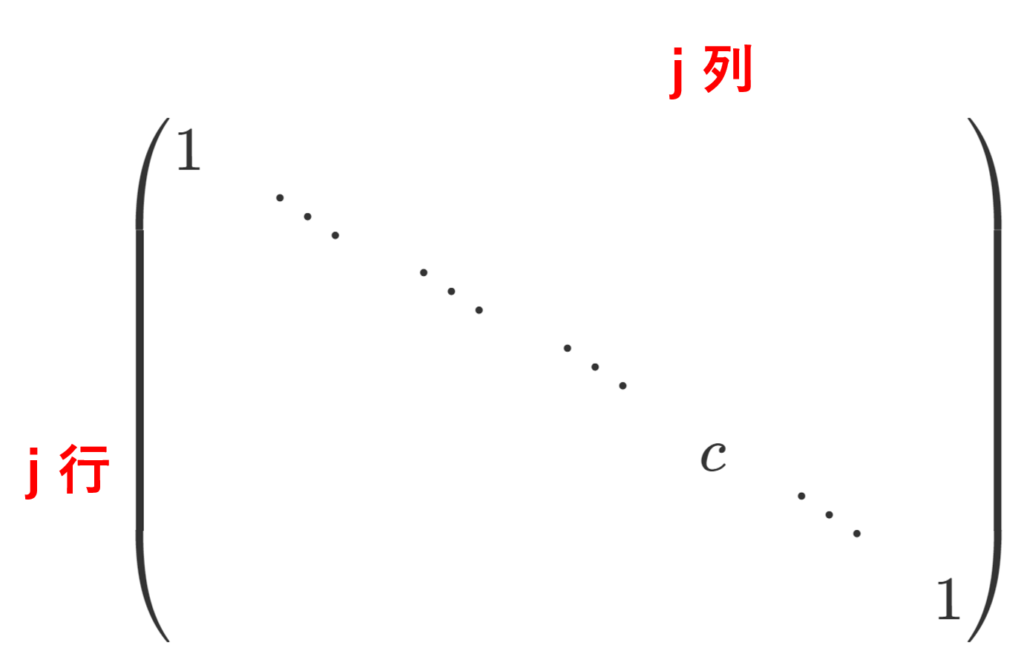
ただし,対角成分で明記のない部分の値は全て 1 で,それ以外の明記のない成分の値は全て 0 である。
上の3つの行列を基本行列 (elementary matrix) と言います。
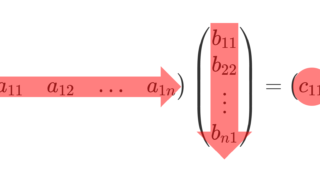
本当にそうなっているかどうかは,実際に計算して確認してみましょう。行列の積の定義について分からない場合は,以下を参照してください。
基本変形による行列式 (det) の変化
ここからは行列式を知っている人向けの話です。
正方行列に対して基本変形を行うと, \det は以下のように変わります。
定理(基本変形と行列式)
正方行列に対し,
- 第 i 行(列)の c 倍を第 j 行(列)に加える変形を行っても行列式は変わらない。
- 第 i 行(列)と第 j 行(列)を入れ替える変形を行うと,行列式は -1 倍になる。
- 第 j 行(列)を c \ne 0 倍する変形を行うと,行列式は c 倍になる。
証明については,以下の記事で触れています。