「サラスの公式」または「サラスの方法」とは,3次正方行列の行列式( \det )を求める記憶術を指します。これについて解説しましょう。
サラスの公式
サラスの公式の定義
定義(サラスの公式)
3 次正方行列の行列式は
\begin{aligned} &\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \\ ={}& a_{11} a_{22}a_{33} - a_{11} a_{23}a_{32} \\ &+ a_{12}a_{23}a_{31} - a_{12}a_{21}a_{33} \\ &+ a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}. \end{aligned}
であるが,これは左上から右下の成分の掛け算を足し,右上から左下の成分の掛け算を引いたものと思える。これをサラスの公式 (サラスの方法; Sarras’ rule) という。
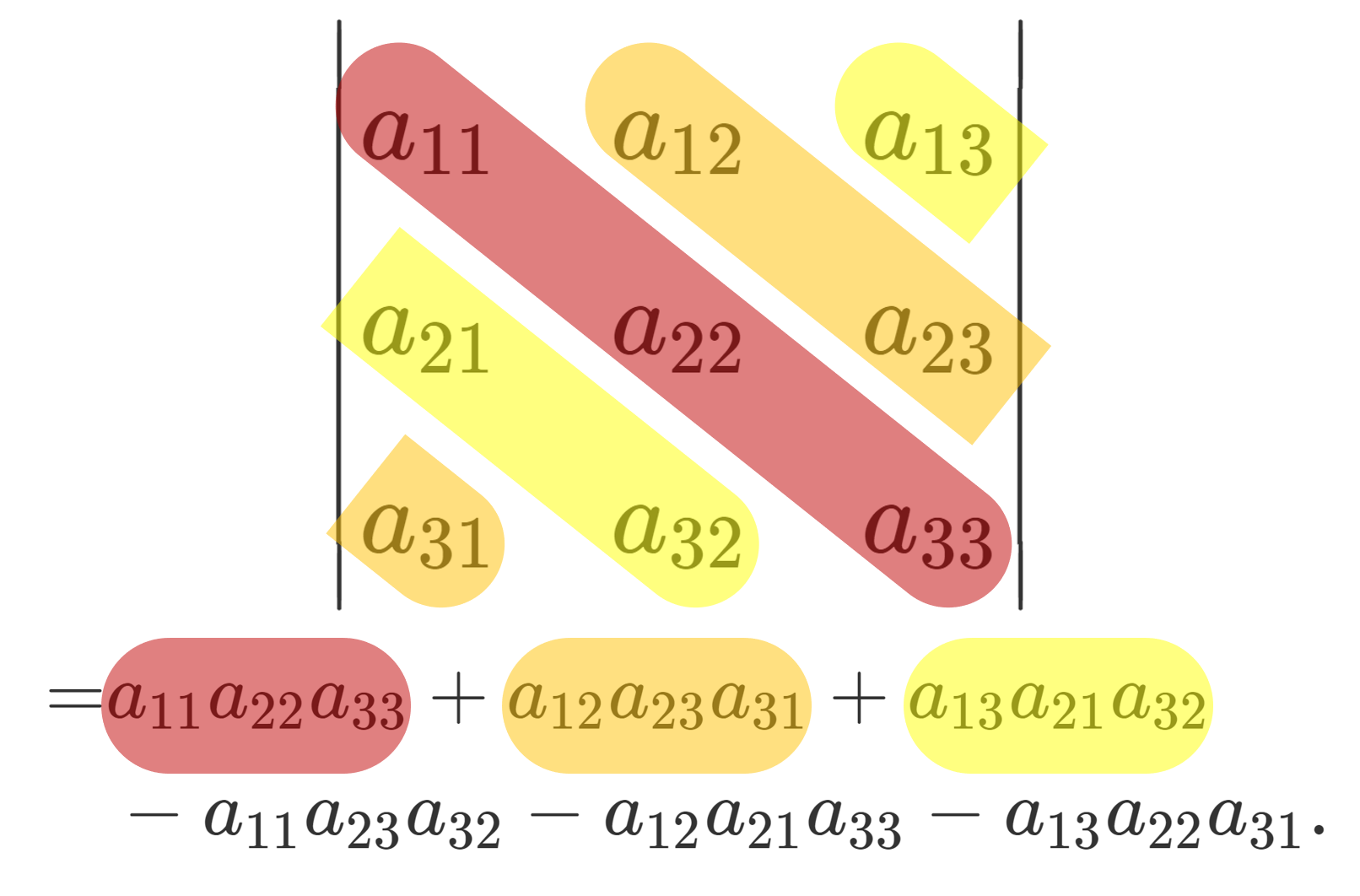
言葉で説明し辛いため,図で示しましょう。
図でのイメージ
左上から右下の成分の掛け算を足すんでした。
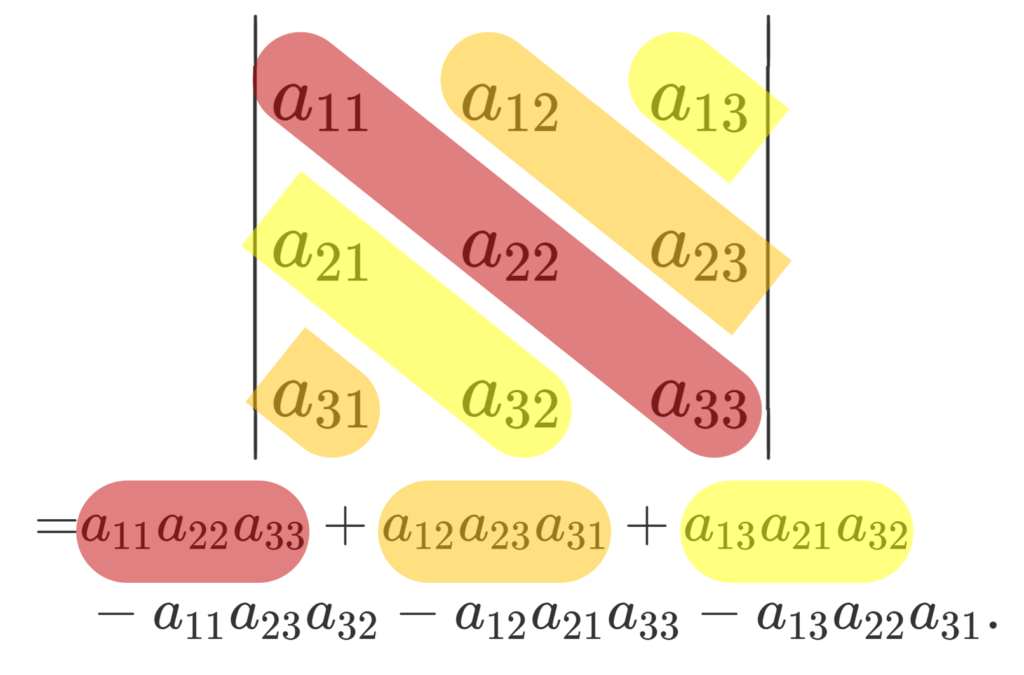
一方で,右上から左下の成分の掛け算を引くんでした。
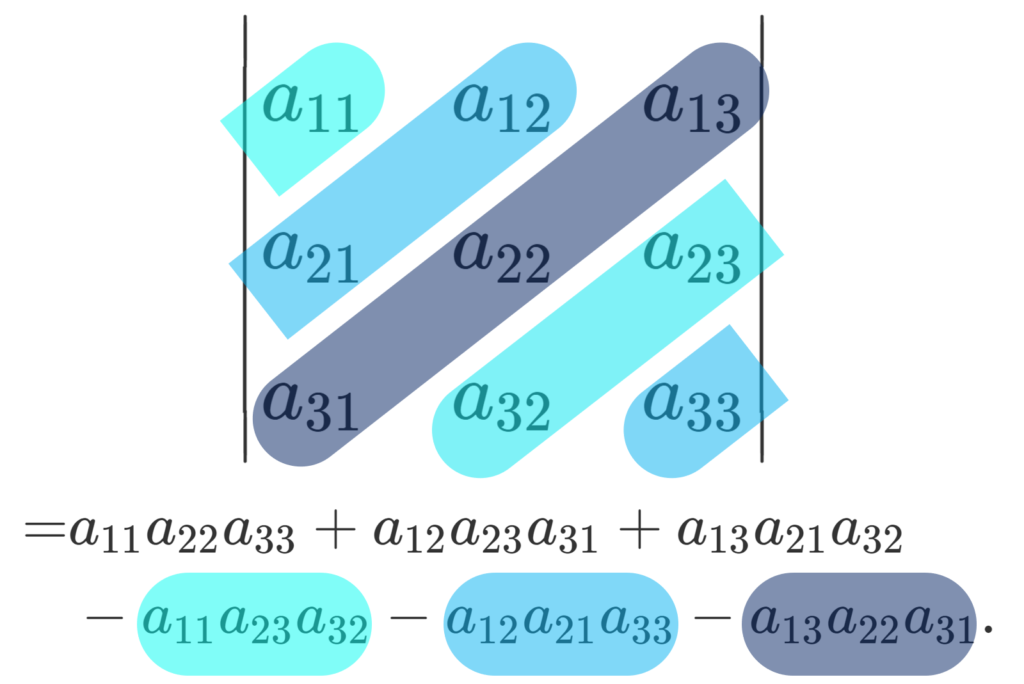
これが,サラスの公式です。
この考え方は,3次の行列に使えますが,4次以上では使えませんので気をつけてください
さいごに注意
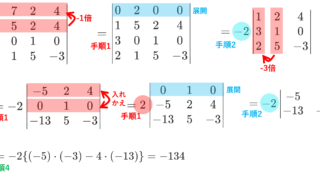
最後に忠告ですが,別にサラスの公式は覚えなくても良いです。3次行列の行列式を計算したい場面はそう多くないため,定義通り計算してもそんなに差し支えないと思います。効率が良いと思うなら覚えるとよいです。
一般の行列式の計算方法は,以下でしっかり解説していますので,そちらも参照してみるとよいでしょう。