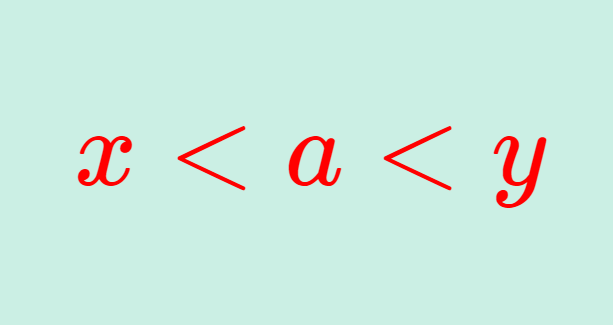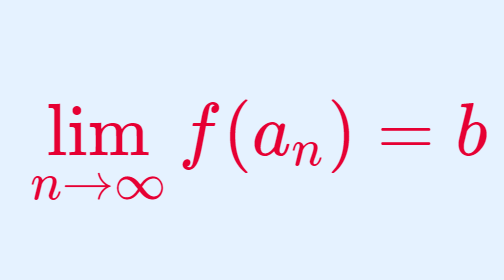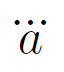大学教養の微分積分学における実数上の稠密性(ちゅうみつせい)の概念について,その定義を紹介し,さらに有理数・無理数が実数上稠密であることを証明します。
実数上における稠密性の定義
まずは実数上における,稠密性の定義を述べましょう。
定義(実数上における稠密性)
A \subset \mathbb{R} とする。 このとき, A が \mathbb{R} 上稠密 (ちゅうみつ, dense) であるとは,
任意の x< y, \,\, x,y\in \mathbb{R} に対して,ある a \in A が存在して,
が成立することをいう。
稠密とは,点の隙間はあってもよいが区間の隙間があってはならない,ある意味「ぎっしり」詰まっている集合といえます。一般に,数直線上に厳密に図示することはできません。
このとき,明らかに以下が成立します。
定理(稠密集合の包含)
A\subset B \subset \mathbb{R} とし, A を \mathbb{R} 上稠密とする。このとき, B も \mathbb{R} 上稠密である。
有理数・無理数は実数上稠密である
定理(有理数・無理数の稠密性)
\mathbb{Q}, \,\, \mathbb{R}\setminus\mathbb{Q} は \mathbb{R} 上稠密である。
すなわち,有理数・無理数は実数上稠密である。
早速証明しましょう。
証明
証明の際,以下の公理を用います(→定義・公理・定理・命題・補題・系を完全理解しよう)。
公理(アルキメデスの原理)
自然数の集合 \mathbb{N} = \{ 1,2,3,\dots\} は上に有界でない。
「公理」としましたが,四則演算・大小関係・実数の連続性を仮定すれば「定理」として従います。
証明していきましょう。
証明
有理数の稠密性
x < y, \,\, x,y \in \mathbb{R} とする。
アルキメデスの原理より, n > 1/(y-x) となる n \in \mathbb{N} が取れる。これにより, ny - nx > 1 が分かる。
再びアルキメデスの原理より, nx < m となる m \in\mathbb{N} を取ると, m, m-1, m-2, \dots のうち, nx < m' をみたす最小の m' (\in \mathbb{Z}) が取れる。このとき m' - nx \le 1 なので,特に nx < m' < ny が従う。よって,
x < \frac{m'}{n} < y
となって, m'/n \in \mathbb{Q} であるから,証明が終わる。
無理数の稠密性
\sqrt{2} は無理数であるから,
\{ \sqrt{2} + r \mid r \in \mathbb{Q}\} \subset \mathbb{R}\setminus \mathbb{Q}
である。左辺は,稠密である有理数の集合を +\sqrt{2} だけ平行移動したものであるから,これも実数上稠密になる。
従って, \mathbb{R} \setminus \mathbb{Q} は実数上稠密である。
証明終
なお,一般に有理数の「数」より無理数の「数」の方が圧倒的に多いことが知られています。
位相空間論における稠密の定義
最後にもっと一般化しましょう。
定義(位相空間論における稠密性)
X を位相空間とする。 A \subset X が稠密 (dense) であるとは, \overline{A} = X が成立することである。ここで, \overline{A} は A の閉包 (closure) を表す。
実数に自然な位相を入れることで,有理数・無理数は稠密であることが分かります。以下で解説しています。