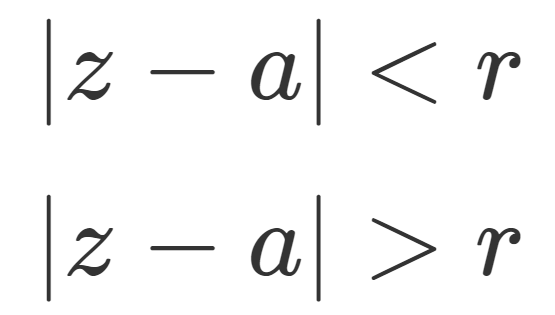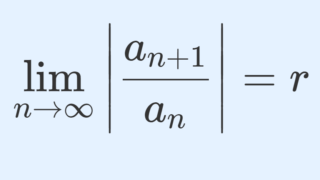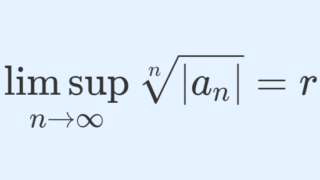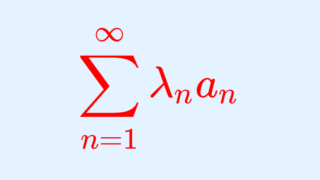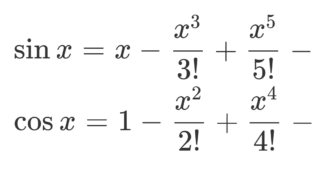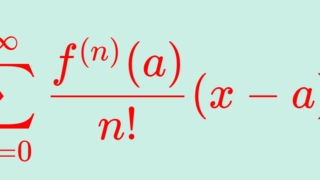べき級数 \displaystyle \sum_{n=0}^\infty a_n x^n , \displaystyle \sum_{n=0}^\infty a_n (z-a)^n における収束半径とは何か定義し,さらにその求め方と具体例について解説します。
収束半径とは
定義(収束半径)
べき級数 \displaystyle \sum_{n=0}^\infty a_n x^n が
- \color{red}|x| < r のとき絶対収束し,
- \color{red} |x| > r のとき発散するとき,
この r を収束半径 (radius of convergence) という。
ただし,すべての x \ne 0 で発散するとき,収束半径は r= 0 と定め,すべての x で収束するときは収束半径は r=\infty と規定する。
最初に注意ですが, |x|=r のときの収束・発散は述べていないことに注意しましょう。 |x|=r では,絶対収束・条件収束・発散のどれもあり得ます。具体例は後ほど述べましょう。
ここで x は実数でなく,複素数でも良いです。加えて 0 を中心としたべき級数ではなく, a\in\mathbb{C} を中心としてもよいです。これを踏まえて,上の定義を一般化しましょう。
定義(収束半径)
べき級数 \displaystyle \sum_{n=0}^\infty a_n (z-a)^n が
- \color{red}|z-a| < r のとき絶対収束し,
- \color{red} |z-a| > r のとき発散するとき,
この r を収束半径 (radius of convergence) という。
ただし,すべての z \ne a で発散するとき,収束半径は r= 0 と定め,すべての z で収束するときは収束半径は r=\infty と規定する。
a=0, x\in \mathbb{R} とすると,最初の定義に一致しますね。
以降は,こちらの一般的な定義の方で進めていきます。
収束半径の求め方
さて,収束判定法の求め方として,
- ダランベールの公式による判定
- コーシーアダマールの公式による判定
の2つを紹介します。
ダランベールの公式による判定
定理(ダランベールの公式)
べき級数 \displaystyle \sum_{n=0}^\infty a_n (z-a)^n に対して,
r =\lim_{n\to\infty} \left|\frac{a_n}{a_{n+1}}\right|\in [0,\infty]
が存在するとき, r は収束半径である。
これは,級数におけるダランベールの収束判定法と関連しています。実際, |z-a|<r としたとき,
\begin{aligned}&\lim_{n\to\infty}\left| \frac{a_{n+1}(z-a)^{n+1}}{a_n(z-a)^n}\right| \\ & =\lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n}\right| |z-a| <\frac{1}{r}\cdot r = 1\end{aligned}
が成立するため,ダランベールの収束判定法により収束します。
ダランベールの収束判定法については,以下の記事を参照してください。
コーシーアダマールの公式による判定
定理(コーシーアダマールの公式)
べき級数 \displaystyle \sum_{n=0}^\infty a_n (z-a)^n に対して,
r = \frac{1}{\displaystyle\limsup_{n\to\infty}\sqrt[n]{|a_n|}}
とすると, r は収束半径である。ただし, 1/\infty = 0, \,1/0 =\infty と解釈する。
コーシーアダマールの公式は,ダランベールの公式より求めるのが難しいです。しかし \limsup は必ず存在するため,これを用いれば収束半径を必ず求めることができます。
本定理は,級数におけるコーシーの収束判定法と関連しています。実際, |z-a|<r としたとき
\begin{aligned} & \limsup_{n\to\infty} \sqrt[n]{|a_n(z-a)^n|} \\ &= \limsup_{n\to\infty} \sqrt[n]{|a_n|}|z-a| < \frac{1}{r} \cdot r = 1 \end{aligned}
が成立するため,コーシーの収束判定法により収束します。
コーシーの収束判定法については,以下の記事を参照してください。
なお本定理から,どんなべき級数でも必ず収束半径が存在することもわかります。すなわち,
- |z-a| < r をみたす任意の z に対して,べき級数は絶対収束する
- |z-a| > r をみたす任意の z に対して,べき級数は発散する
の両方を同時に満たす 0\le r \le \infty は必ず存在することがわかります。
収束半径の具体例
収束半径を求める具体例を挙げましょう。またそれと同時に, |x|=r のときにどうなるかも考えてみましょう。
例1.
\displaystyle\color{red} \sum_{n=0}^\infty \frac{1}{2^n} x^n の収束半径は r = 2 である。
これは,ダランベールの判定法を用いて,
\left|\frac{1/2^n}{1/2^{n+1}}\right| =2
であることから従います。
このことより, |x|< 2 では絶対収束し, |x|> 2 のとき発散することが分かりました。ところで, |x|=2 のときはどうなるのでしょうか? 結論,今回の場合は |x| = 2 のときは発散します。
実際, |x|=2 とすると,各項について |\frac{1}{2^n} x^n| = 1 となって 0 に収束しないため,収束することはありません。
例2.
\displaystyle\color{red} \sum_{n=1}^\infty \frac{1}{n} x^n の収束半径は r = 1 である。
これは,ダランベールの判定法を用いて,
\begin{aligned}\left|\frac{1/n}{1/(n+1)} \right| &= \left|\frac{n+1}{n} \right| \xrightarrow{n\to\infty} 1 \end{aligned}
であることから従います。
このことより, |x|< 1 では絶対収束し, |x|> 1 のとき発散することが分かりました。では, |x|=1 のときはどうなるのでしょうか? 結論,今回の場合は x=1 のときは発散し, x=e^{i\theta} \,(\theta \notin \{2m\pi \mid m \in\mathbb{Z} \}) のとき(すなわち |x|=1 かつ x\ne 1 のとき)は条件収束します。
これについては,以下の記事で解説していますから,参照してください。
例3.
\color{red} \sin x=x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots
の収束半径は r = \infty である。
\sin のマクローリン展開ですね。テイラー展開・マクローリン展開においては,収束半径の議論は避けては通れないでしょう。
収束半径については,コーシーアダマールの公式を用いて,
\begin{aligned}\limsup_{n\to\infty} \sqrt[n]{\frac{1}{n!}} & \le \left(\frac{2}{n-1}\right)^{\frac{n-1}{2} \cdot \frac{1}{n}} \\ &\le \sqrt[4]{\frac{2}{n-1}} \xrightarrow{n\to\infty} 0 \end{aligned}
であることから,逆数を取ることでわかります。(実際の頭の中では \frac{(n+1)!}{n!} = n+1 を考えて,ダランベールの公式を当てはめているんですけどね。)
\sin のマクローリン展開ついては,以下で解説しています。
テイラー展開・マクローリン展開そのものに関しては,以下で解説しています。