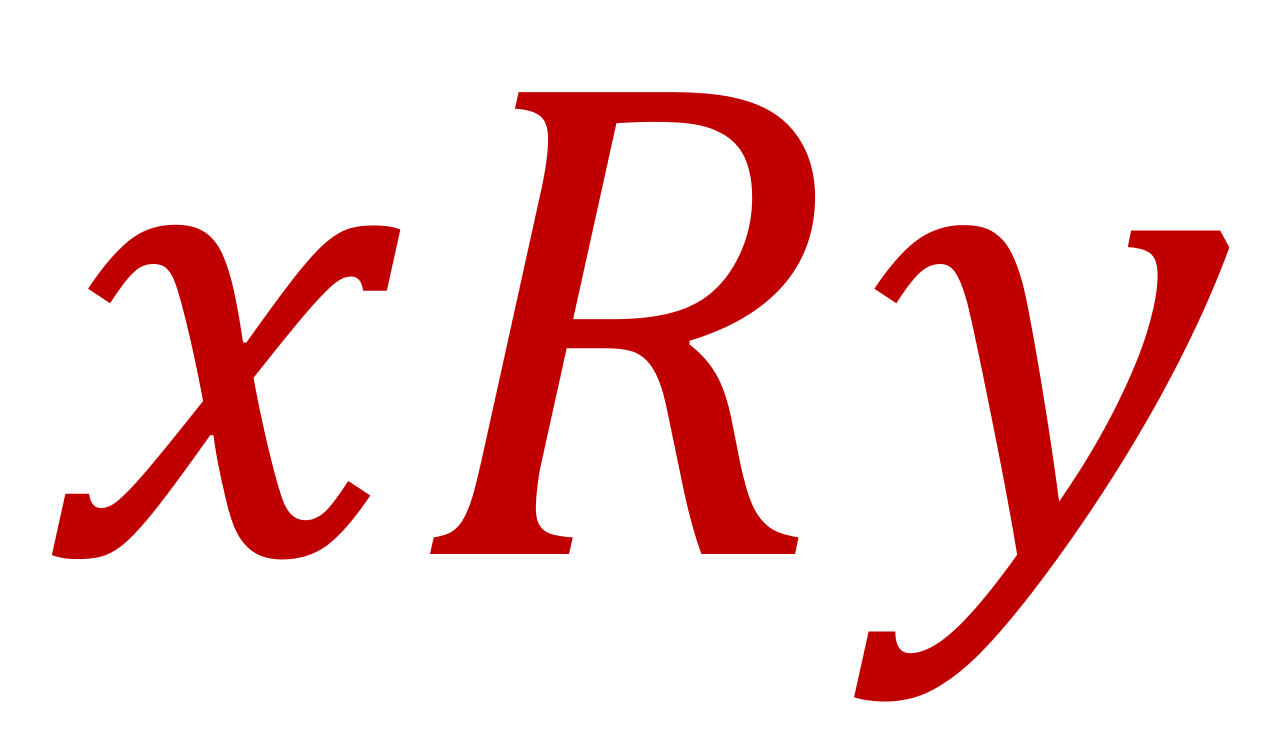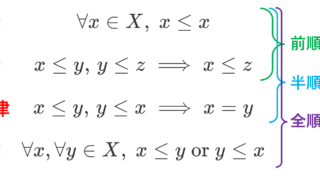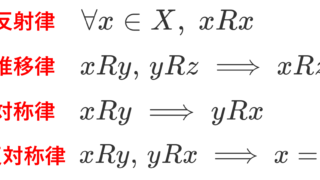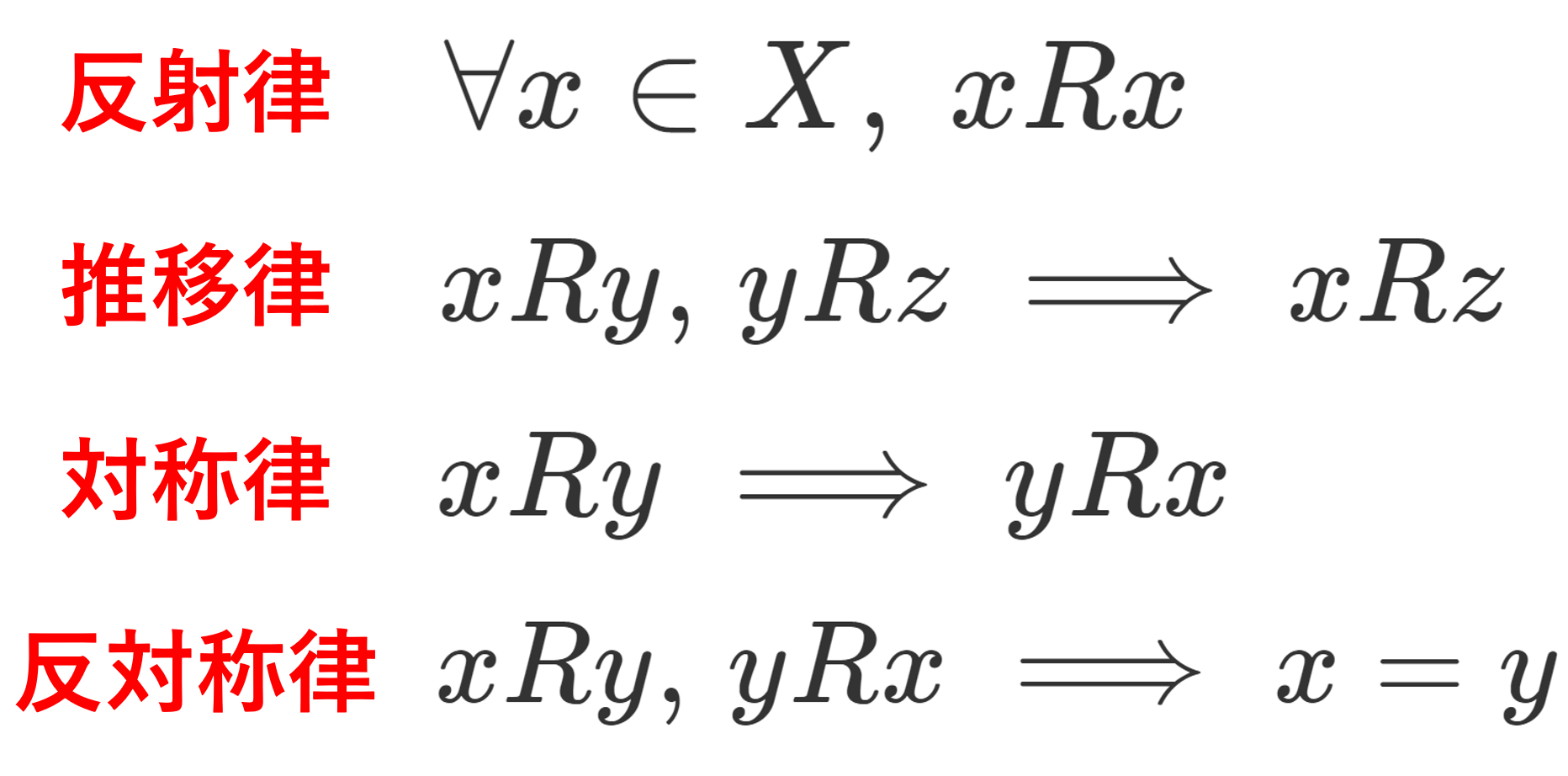二項関係とは

数学における，集合上の２つの元の関係を表す「二項関係」について，その定義と具体例を解説します。

ある集合 $A$ があったとしましょう。この2つの元 $x,y\in A$ に対し，何らかの「関係」が定まっているとします。このとき， $x,y$ には関係があるといいます。

このように，ある集合の2つの元に定める「関係」を，二項関係といいます。

たとえば， $A$ を人間たちの集合とします。人 $x,y\in A$ が友達であるとき， $x,y$ は「関係がある」と言うことにしましょう。これが「二項関係」です。
この関係に名称をつけるなら「友達関係」ですね。友達でない二人の人には，「友達関係はない」ですね。

他にも，人間同士には，「知り合いの関係」「部下と上司の関係」「同僚の関係」「同国籍の関係」など，さまざまな関係を定めることができそうですね。

あるいは， $\mathbb{R}$ を実数の集合としましょう。この上には， $x,y$ に対して， $x\le y$ あるいは $y\le x$ という「二項関係」が定まっています。
これを順序関係（大小関係）と言ったりします。

二項関係の厳密な定義

1つの集合の上には，いろいろな「二項関係」を考えることが可能ですから，一般に数学において「二項関係」を定義するときは，関係があるかないかのみを定義します。

関係があるかないかを数学的に厳密に定義したいとしましょう。果たしてどうすればよいでしょうか。厳密な定義を見てみましょう。

定義（二項関係）

$R$ が $A$ 上の二項関係 (binary relation) であるとは，直積集合 $A^2=A\times A$ の部分集合

\color{red}R\subset A\times A

のことである。 $(x,y)\in R$ のことを， $\color{red}xRy$ ともかく。

$R$ という記号を持ちましたが，実際は $\sim, \le$ をはじめ，さまざまな記号が用いられます。

ちょっと定義に戸惑ったかもしれません。数学的に「2つの関係」の有無を定義しようと思うと，関係があれば属するような集合を考えるというわけです。

$(x,y)\in R$ なら $xRy$ という関係があると考え， $(x,y)\notin R$ なら，そのよう関係がないと考えるわけですね。

たとえば， $\mathbb{R}$ 上の順序関係（大小関係） $R$ は，集合でかけば

R=\{ (x,y)\in\mathbb{R}^2\mid x\le y\}

とかけます。

なお，実際は $x,y$ は別の集合に属していてもよく，たとえば $R \subset A\times B$ とすることで， $A,B$ 間の二項関係を考えることもできます。

ただ，やはり「関係」を考えるにあたっては，それがどんな関係かは気になるところでしょう。実際，数学では名前の付くような特別な「関係」を考察することで，議論が進められます。ここでは，代表的な２つの「二項関係」をみていきましょう。

二項関係の例1((半)順序関係).

$A$ 上の二項関係 $R$ が以下を全てみたすとき，(半)順序関係という。

関係に $R$ という記号を用いましたが，順序関係には普通 $\le$ という記号を用いて， $x\le y$ とかかれます。実際，実数上の順序関係（大小関係）は，上の3つの関係をみたしますね。

順序関係については，以下で解説しています。

二項関係の例2(同値関係).

$A$ 上の二項関係 $R$ が以下を全てみたすとき，同値関係という。

同値関係は，「同じものである」と思える関係のことです。関係には，よく $\sim$ という記号を用いて， $x\sim y$ という風にも書かれます。これについては，以下で解説しています。