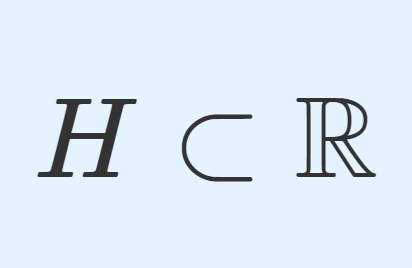 線形代数学
線形代数学 ハメル基底とは~有理数上実数の基底~
ハメル基底 (Hamel basis)とは,実数を有理数上のベクトル空間とみなしたときの基底のことを言います。ハメル基底についてその定義と濃度,関連する話題を紹介しましょう。
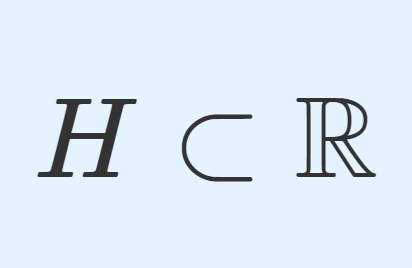 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 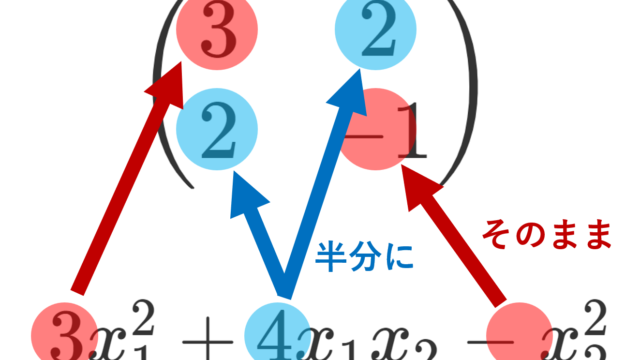 線形代数学
線形代数学 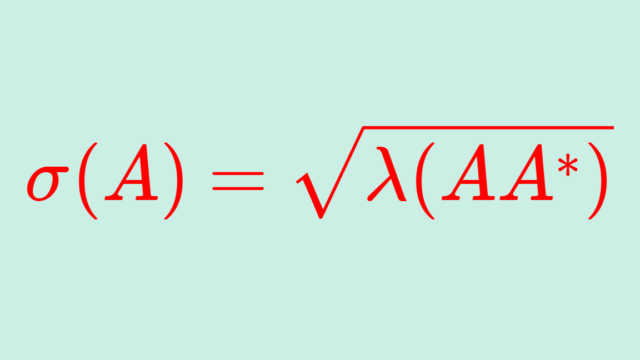 線形代数学
線形代数学  線形代数学
線形代数学 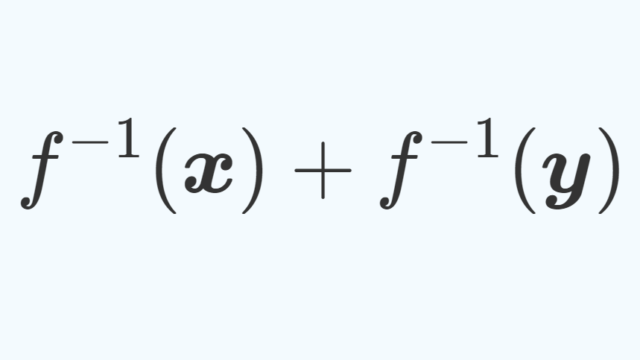 線形代数学
線形代数学 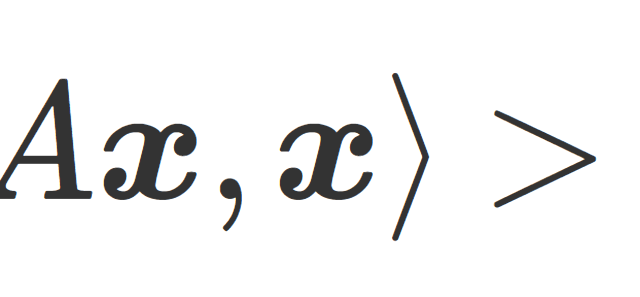 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学