 線形代数学
線形代数学 行列の基本変形についてわかりやすく図解する
行列の行基本変形・列基本変形について,定義と基本行列 (elementary matrix) との演算対応,行列式との関係について順に,図を用いながら解説していきます。
 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 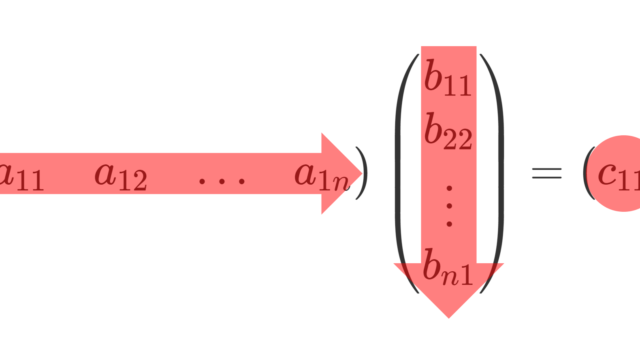 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学