 解析学(大学)その他
解析学(大学)その他 凸包とは何か~定義と具体例と性質~
集合Aの凸包 (convex hull) とは,Aを含む最小の凸集合を指します。これについて,定義と具体例と性質を述べましょう。
 解析学(大学)その他
解析学(大学)その他 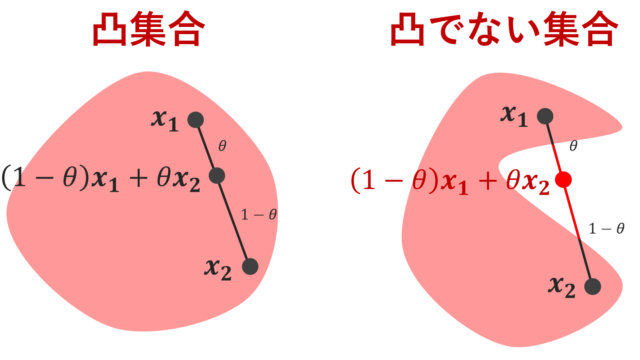 解析学(大学)その他
解析学(大学)その他 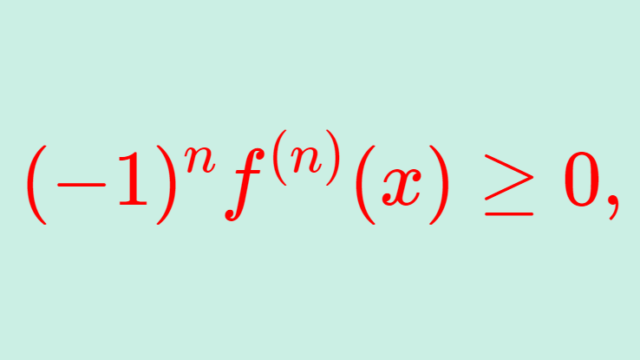 解析学(大学)その他
解析学(大学)その他 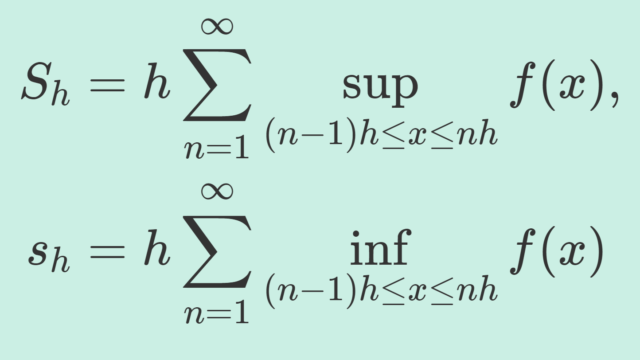 解析学(大学)その他
解析学(大学)その他 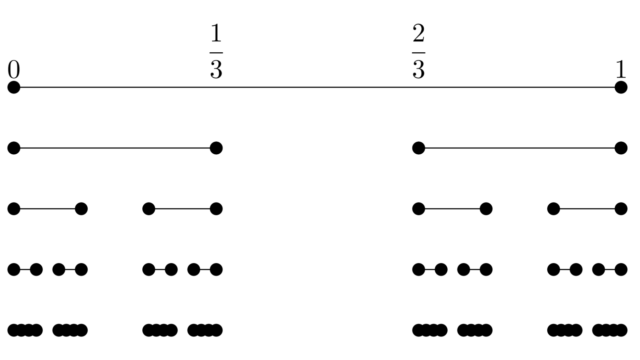 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他