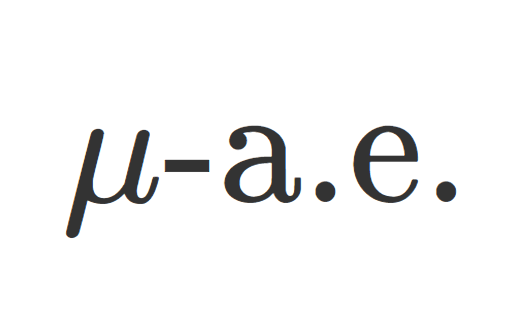 測度論
測度論 ほとんどいたるところ(almost everywhere, a.e.)の議論
測度論においては,ほとんどいたるところ(almost everywhere, a.e.)を用いた議論が頻繁に出てきます。 「ほとんどいたるところ」の定義と具体例について,丁寧に解説しましょう。
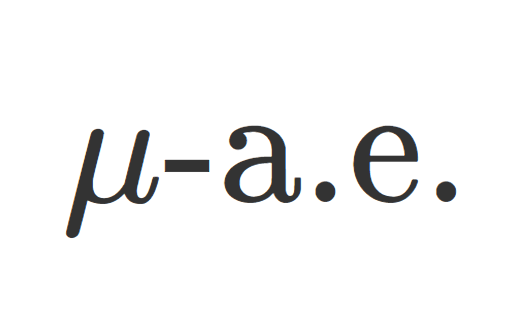 測度論
測度論 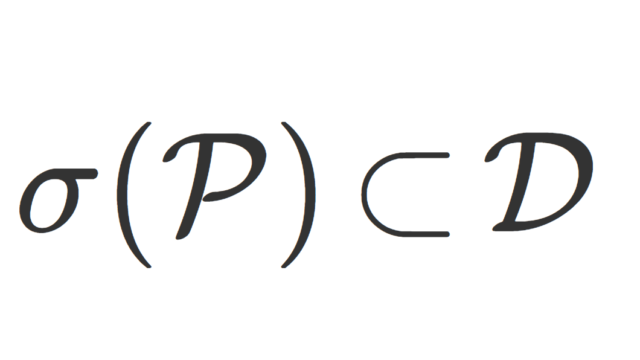 測度論
測度論 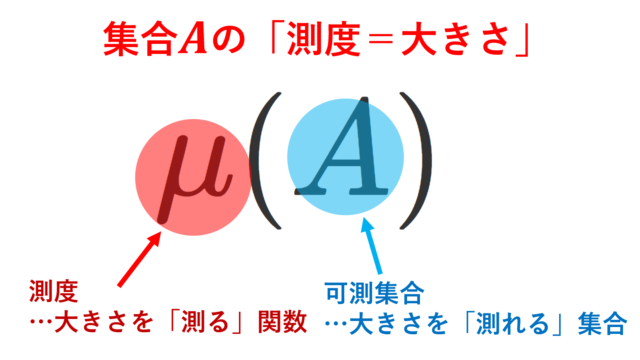 測度論
測度論 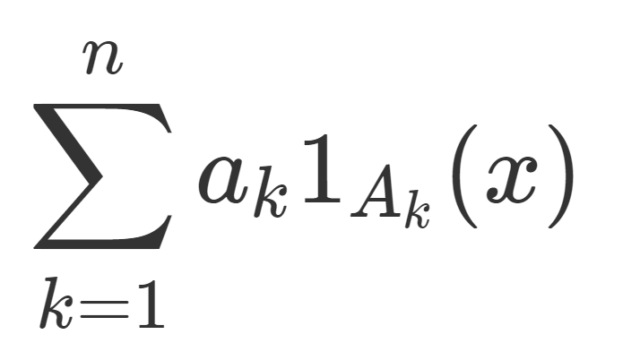 測度論
測度論 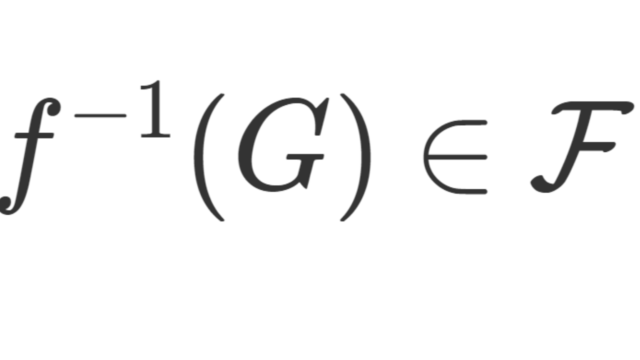 測度論
測度論 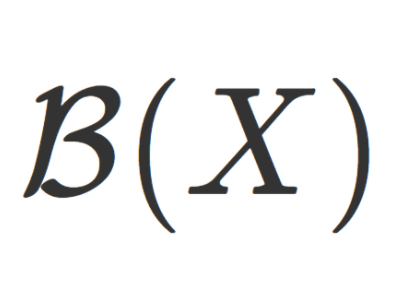 測度論
測度論 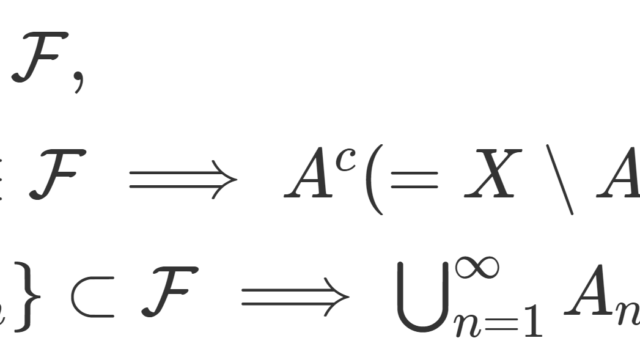 測度論
測度論