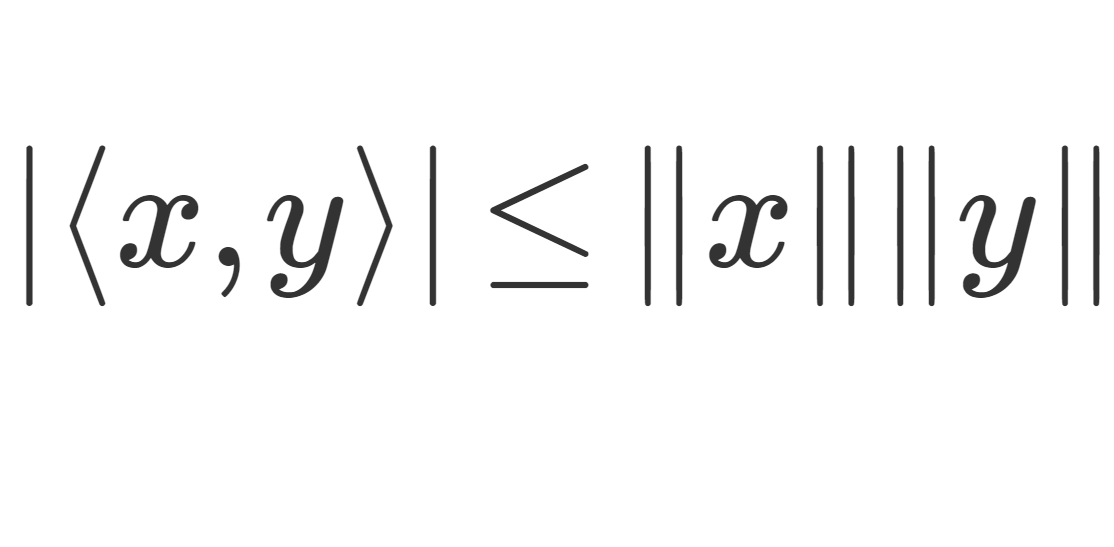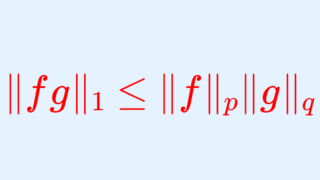コーシーシュワルツの不等式 (Cauchy-Schwarz inequality) とは,コーシーさんとシュワルツさんが編み出した不等式で,現代においては高校数学から専門数学まで幅広い範囲で使われています。高校では,
(a_1b_1+a_2b_2)^2\le (a_1^2+a_2^2)(b_1^2+b_2^2)
や
のような形が有名でしょう。これについて,まずは専門数学の最も一般的な形で定理の主張を述べ,それから上の例を含むより具体的な形を紹介してから,最後に証明を記述しましょう。等号成立条件についても扱います。
コーシーシュワルツの不等式
ここでは,コーシーシュワルツの不等式をかなり一般的な形で述べます。高校生の場合は,そういうものかと流して,次に進むとよいと思います。
内積空間は,複素数 \mathbb{C} 上で考えるものとします。内積空間とは,内積が定義されたベクトル空間のことです。本記事では,x,y の内積は \color{red} \langle x,y\rangle と記述します。
定理(コーシーシュワルツの不等式)
X を内積空間とする。このとき,任意の x,y\in X に対し,
\Large \color{red} |\langle x,y\rangle |\le \|x\| \|y\|
が成立する。等号成立は x=0 または y=kx\;(k\in\mathbb{C}) と表せるとき(すなわち一次独立でないとき)に限る。
左辺は絶対値を忘れないでください。一般に内積は複素数です。不等式を言い換えて,
\large \color{red} |\langle x,y\rangle |^2\le \langle x,x\rangle \langle y,y\rangle
としてもよいです。コーシーシュワルツの不等式は単にシュワルツの不等式ということも多いです。
数学専攻でないと,上の意味はよく分からないかもしれません。とにかく具体例を見てみましょう。
コーシーシュワルツの不等式のさまざまな形
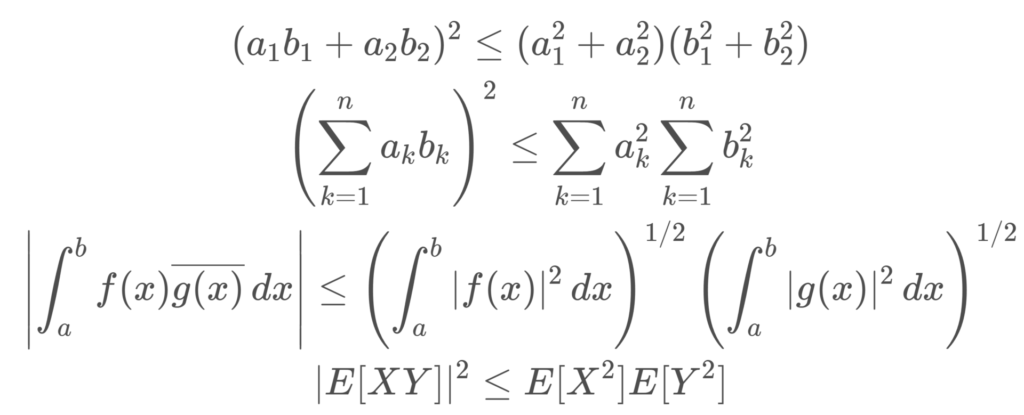
高校でよく見る和の形のコーシーシュワルツの不等式
系1(和の形のコーシーシュワルツの不等式)
a_1,a_2,b_1,b_2\in\mathbb{R} に対して,
\color{red} (a_1b_1+a_2b_2)^2\le (a_1^2+a_2^2)(b_1^2+b_2^2)
が成り立つ。等号成立は a_1=a_2=0 または b_1=ka_1,\,b_2=ka_2 を同時にみたす k\in\mathbb{R} が存在するときである。
より一般に, a_1,\dots, a_n,b_1,\dots, b_n\in\mathbb{R} に対して,
\color{red}\left(\sum_{k=1}^n a_kb_k\right)^2\le \sum_{k=1}^n a_k^2 \sum_{k=1}^n b_k^2
が成立する。等号成立は a_1=\dots=a_n=0 または b_1=ka_1,\dots, b_n=ka_n を同時にみたす k\in\R が存在するときである。
コーシーシュワルツの不等式の定理で, x=(a_1,a_2),\; y=(b_1,b_2)\in\R^2 とおいたものが一つ目で, x=(a_1,\dots, a_n),\; y=(b_1,\dots, b_n)\in\R^n とおいたものが二つ目です。数ベクトルのノルム・内積の話ですね。
実数のみ扱っていますが,複素数の場合,すなわち x=(a_1,\dots, a_n),\; y=(b_1,\dots, b_n)\in\mathbb{C}^n のときは,
\color{red}\left|\sum_{k=1}^n a_k\overline{b_k}\right|^2\le \sum_{k=1}^n |a_k|^2 \sum_{k=1}^n |b_k|^2
となります。また, x=(a_1,a_2,\dots), \; y=(b_1,b_2,\dots ) を \sum_{n=1}^\infty a_n^2<\infty,\; \sum_{n=1}^\infty b_n^2<\infty をみたす無限実数列として,
とすることもできます。専門数学的に言えば,これは2乗和が収束する数列空間 \ell^2(\mathbb{R}) におけるコーシーシュワルツの不等式です。
他にも,高校でよく見るコーシーシュワルツの不等式として, \color{red} |\vec{a}\cdot\vec{b}|\le |\vec{a}||\vec{b}| が挙げられると思います。高校で扱うベクトルは平面ベクトルか空間ベクトルであり, \vec{a}=(a_1,a_2) のように成分表示できますから,上と同じですね。
積分型のコーシーシュワルツの不等式
系2(積分型のコーシーシュワルツの不等式)
f,g \in C[a,b] すなわち f,g\colon [a,b]\to\mathbb{C} は [a,b] における連続関数とする。このとき,
\color{red}\begin{aligned}&\left|\int_a^b f(x)\overline{g(x)}\,dx\right|\\&\le\left( \int_a^b |f(x)|^2\,dx\right)^{1/2}\left(\int_a^b |g(x)|^2\,dx\right)^{1/2}\end{aligned}
が成り立つ。等号成立は, f(x)\equiv 0 または g(x)=k f(x) \;(x\in[a,b]) となる k\in\mathbb{C} が存在するときである。
ベクトル空間 C[a,b] に \langle f,g\rangle = \int_a^b f(x)\overline{g(x)}\, dx と内積を入れたものです。
より一般に,関数 f,g\colon \R\to\mathbb{C} が \int_\R |f(x)|^2\,dx<\infty,\; \int_\R |g(x)|^2\,dx<\infty をみたすとしたとき,
\color{red}\begin{aligned}&\left|\int_\R f(x)\overline{g(x)}\,dx\right|\\&\le\left( \int_\R |f(x)|^2\,dx\right)^{1/2}\left(\int_\R |g(x)|^2\,dx\right)^{1/2}\end{aligned}
が成り立ちます。関数解析の専門的な言葉を用いて言うと,これは L^2(\R) におけるコーシーシュワルツの不等式です。さらに,より一般の測度における積分でも同様のことが成立します。
相関係数の値が -1≦r≦1 であること
確率論・統計学においても,コーシーシュワルツの不等式は登場します。
系3(確率変数におけるコーシーシュワルツの不等式)
X,Y を実数値確率変数とし,E[\cdot] で期待値を表すとする。いま, E[X^2],\, E[Y^2]<\infty とすると,
\color{red}|E[XY]|^2\le E[X^2]E[Y^2]
が成り立つ。
期待値の計算は,和や積分の計算に帰着できます。よって,これは,和や積分におけるコーシーシュワルツの不等式のちょっとした応用になっています。
いま, \mu=E[X],\;\nu=E[Y] をそれぞれ X,Y の期待値(平均)とすると,分散・共分散はそれぞれ,
\begin{aligned}\operatorname{Var}(X)&= E[(X-\mu)^2],\\\operatorname{Var}(Y)&= E[(Y-\nu)^2], \\ \operatorname{Cov}(X,Y)&=E[(X-\mu)(Y-\nu)]\end{aligned}
と表せます。一番下の式にコーシーシュワルツの不等式を適用すると,
となります。すなわち,
ですね。 \frac{\operatorname{Cov}(X,Y)}{\sqrt{\operatorname{Var}(X)}\sqrt{\operatorname{Var}(Y)}} というのは, X,Y の相関係数の定義そのものでしたから,これは,相関係数 r が -1\le r\le 1 をみたすことの証明になっているわけです。
コーシーシュワルツの不等式の証明
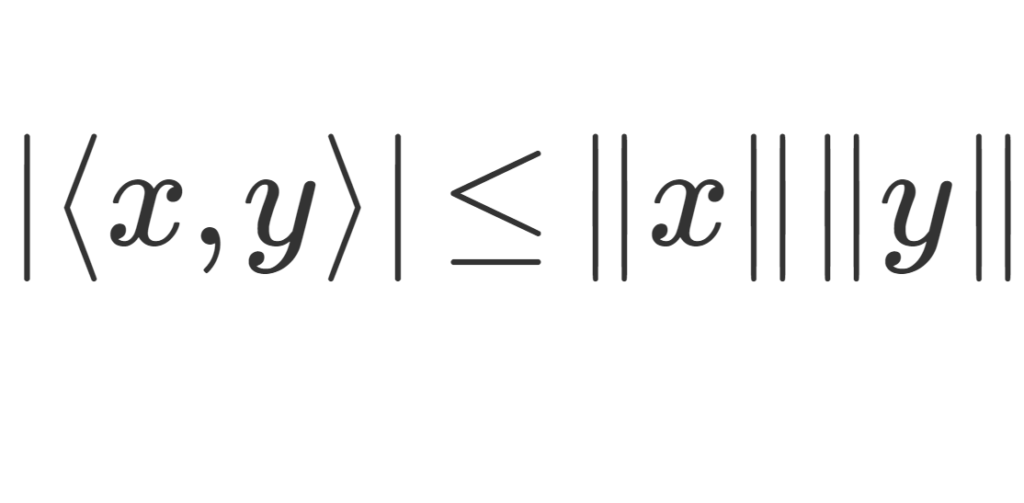
さて,最後にコーシーシュワルツの不等式の証明をしておきましょう。はじめの定理を再掲します。
定理再掲(コーシーシュワルツの不等式)
X を内積空間とする。このとき,任意の x,y\in X に対し,
\Large |\langle x,y\rangle |\le \|x\| \|y\|
が成立する。等号成立は x=0 または y=kx\;(k\in\mathbb{C}) と表せるとき(すなわち一次独立でないとき)に限る。
証明は少々テクニカルです。
証明
x=0 または y=0 のときは等号が明らかに成り立つ。従って,x,y\ne 0 としてよい。
|\langle x,y\rangle |\le \|x\| \|y\| について
\theta = \arg \langle x,y\rangle すなわち \theta を \langle x,y\rangle の偏角とすると, \langle x,y\rangle=e^{i\theta} |\langle x,y\rangle| である。
x'=e^{-i\theta} x と定める。任意の t\in\R に対し,不等式
\begin{align}0&\le \|x'-ty\|^2\\&=\langle x',x'\rangle-2t \operatorname{Re} \langle x',y\rangle+t^2 \langle y,y\rangle \end{align}
が成立する。 y\ne 0 と仮定したため, (2) 式は2次式であることに注意して,この判別式について,
が成り立つ。ここで, \operatorname{Re} \langle x',y\rangle=\operatorname{Re} e^{-i\theta}\langle x,y\rangle =| \langle x,y\rangle| と, \langle x',x'\rangle=\langle x,x\rangle より,
となるので,結論を得る。
等号成立について
等号成立 \implies y=kx となる k\in\mathbb{C} が存在について
『 (4) 式で等号成立 \iff (3) 式で等号成立 \iff「 (1) 式で等号成立する t=t_0\in\R が存在する」』であり,等号成立するときは y=t_0x' = t_0e^{-i\theta}x となる。 k=t_0e^{-i\theta}\in\mathbb{C} とおけばよい。
y=kx \implies 等号成立について
y=kx となる k\in\mathbb{C} が存在するときは,
\!\!\!\!|\langle x,y\rangle|^2 = |k\langle x,x\rangle|^2= \|x\|^2\|kx\|^2=\|x\|^2\|y\|^2
となるため,等号は成立する。
証明終
二次式の判別式を考えるところがミソです。
コーシーシュワルツの不等式はヘルダーの不等式の特別なもの
さて,和の形のコーシーシュワルツの不等式
\left(\sum_{n=1}^\infty a_nb_n\right)^2\le \sum_{n=1}^\infty a_n^2 \sum_{n=1}^\infty b_n^2
と積分の形のコーシーシュワルツの不等式
を思い出してください。これらは,より一般に以下が成り立つことが知られています
定理(ヘルダーの不等式)
1<p,q<\infty,\; 1/p+1/q=1 とする。
複素数列 \{a_n\},\,\{b_n\}\subset\mathbb{C} がそれぞれ \sum_{n=1}^\infty |a_n|^p<\infty,\; \sum_{n=1}^\infty |b_n|^q<\infty をみたすとき,
\color{red}\sum_{n=1}^\infty |a_nb_n|\le\left(\sum_{n=1}^\infty |a_n|^p\right)^{1/p}\left(\sum_{n=1}^\infty |b_n|^q\right)^{1/q}
が成り立つ。また,関数 f,g\colon \R\to\mathbb{C} が \int_\R|f|^p\,dx<\infty,\; \int_\R |g|^q\,dx<\infty をみたすとき,
が成り立つ。
ヘルダーの不等式において p=2 としたものが,コーシーシュワルツの不等式になるわけです(実際は |\sum a_n\overline{b_n}|\le \sum|a_nb_n| も使っています)。ヘルダーの不等式の証明については,以下で解説しています。