巡回行列式の計算

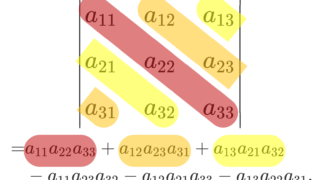
特殊で有用な行列式の計算の一つに，巡回行列における行列式の計算が挙げられるでしょう。これについて紹介します。

巡回行列とは

まずは巡回行列を定義します。

定義（巡回行列）

\color{red} \begin{pmatrix} x_0 & x_1 & x_2 &\dots & x_{n-1} \\ x_{n-1} & x_0 & x_1 & \dots & x_{n-2} \\ x_{n-2} & x_{n-1} & x_0 & \dots & x_{n-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_1 & x_2 & x_3 & \dots & x_0 \end{pmatrix}

の形の $n$ 次正方行列を巡回行列 (circulant matrix) という。

各成分がくるくる回って「巡回」していますね。

上のような巡回行列の行列式は，以下のようになることが知られています。

定理（巡回行列式）

\color{red} \begin{aligned} &\begin{vmatrix} x_0 & x_1 & x_2 &\dots & x_{n-1} \\ x_{n-1} & x_0 & x_1 & \dots & x_{n-2} \\ x_{n-2} & x_{n-1} & x_0 & \dots & x_{n-3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_1 & x_2 & x_3 & \dots & x_0 \end{vmatrix} \\ &= \prod_{\zeta} (x_0 + \zeta x_1 + \zeta^2 x_2 + \dots \zeta^{n-1} x_{n-1} ) \end{aligned}

である。ただし， $\zeta$ は $1$ の $n$ 乗根全体にわたる。

早速証明しましょう。

証明には，行列の基本変形とそのときの行列式の変化の法則を用います。これについて詳しくは行列式(det)の定義と現実的な求め方～計算の手順～も参照してください。

証明

$\zeta$ を $1$ の $n$ 乗根の一つとする。行列式の第 $i$ 列 $( i=2,3\dots,n )$ に $\zeta^{i-1}$ を掛けたものを第 $1$ 列に加えることで，

\begin{aligned} &\begin{vmatrix} x_0 & x_1 &\dots & x_{n-1} \\ x_{n-1} & x_0 & \dots & x_{n-2} \\ x_{n-2} & x_{n-1} & \dots & x_{n-3} \\ \vdots & \vdots & \ddots & \vdots \\ x_1 & x_2 & \dots & x_0 \end{vmatrix} \\ &= \begin{vmatrix} \sum_{k=0}^{n-1} \zeta^k x_k& x_1 &\dots & x_{n-1} \\ \zeta \sum_{k=0}^{n-1} \zeta^k x_k & x_0 & \dots & x_{n-2} \\ \zeta^2 \sum_{k=0}^{n-1} \zeta^k x_k & x_{n-1} & \dots & x_{n-3} \\ \vdots & \vdots & \ddots & \vdots \\ \zeta^{n-1} \sum_{k=0}^{n-1} \zeta^k x_k & x_2 & \dots & x_0 \end{vmatrix} \end{aligned}

がわかる。よって，求める行列式は

\sum_{k=0}^{n-1} \zeta^k x_k = x_0 + \zeta x_1 + \zeta^2 x_2 + \dots \zeta^{n-1} x_{n-1}

で割り切れる。 $1$ の全ての $n$ 乗根についてこのことが分かるから，因数定理により求める行列式は

\prod_{\zeta} (x_0 + \zeta x_1 + \zeta^2 x_2 + \dots \zeta^{n-1} x_{n-1} )

で割り切れる。これは $n$ 次式であるから，求める行列式はこれ以上因数を持たない。求める行列式は上の定数倍であり，求める行列式の $x_0^n$ の係数は $1$ であるから，結局上の式そのものが求める行列式である。

証明終

その他の特殊で有用な行列式には，以下のようなものがあります。

一般の行列式の性質については，以下の記事を参照してください。