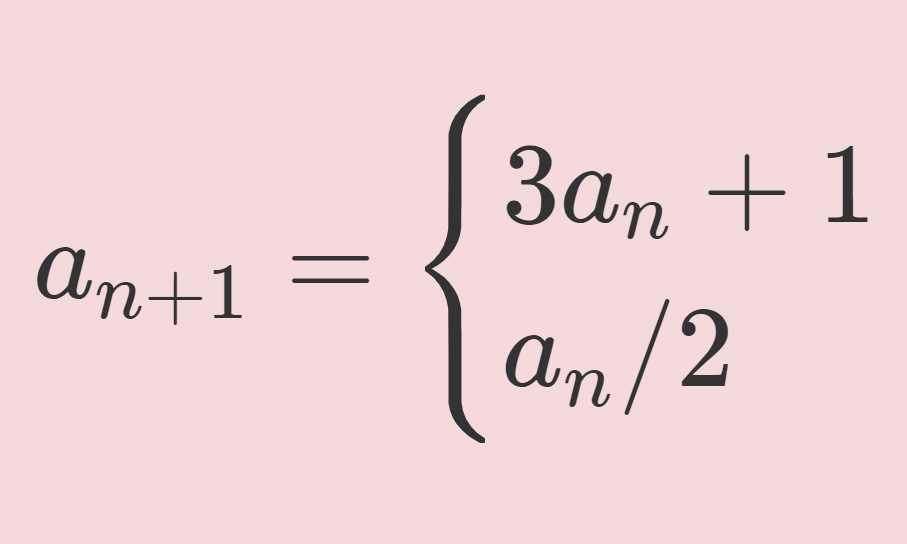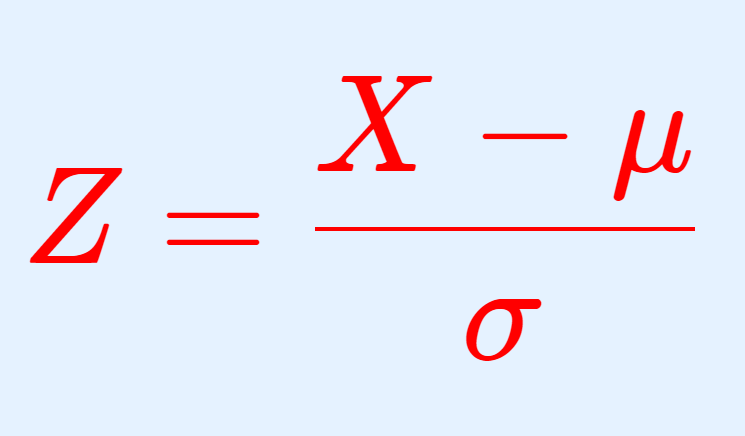コラッツ予想（コラッツの問題）とは

コラッツ予想（コラッツの問題; Collatz conjecture; 角谷予想）は，整数論に関する予想で，主張自体は中高生でも理解できそうなくらい簡単にもかかわらず，多くの数学者の頭を悩ませる未解決問題の1つとして有名です。これについて，その主張を解説しましょう。

コラッツ予想とは
コラッツ予想を解こう

コラッツ予想とは

まずは，コラッツ予想の主張を確認しましょう。「予想」なので，正しいか正しくないかが分かっていません。未解決問題なのです。

コラッツ予想の主張

コラッツ予想 (Collatz conjecture)

$a$ を正の整数とする。 $a_1 = a$ とし，以下の式によって，数列 $\{a_n\}$ を定める。

a_{n+1} = \begin{cases} 3a_n +1 &\text{if } a_n \text{ is odd,} \\ a_n / 2 &\text{if } a_n \text{ is even.} \end{cases}

このとき，任意の $a$ に対して， $a_m = 1$ となる $m$ が存在する。（oddは「奇数」，evenは「偶数」を指す）

別の言葉で換言すると，正の整数 $a$ をスタートし，

奇数ならば3倍して1を足す
偶数ならば2で割る

ことを繰り返すと，いずれ必ず $1$ になるといえます。

このように，中高生でも理解できそうな簡明な主張にもかかわらず，80年以上も多くの数学者の頭を悩ませる「難しい問題」であり，時折進展があったとか無かったとかいう話を耳にすることはあるものの，正しいか正しくないかは未だ不明です。

具体例を挙げましょう。

コラッツ予想の具体例

例1.

$a = 3$ とすると，

3\to 10 \to 5 \to 16\to 8\to 4\to 2 \to 1

となって $7$ 回のステップで $1$ に到達する。

例2.

$a=11$ とすると，

11\to 34\to 17\to 52\to 26\to 13 \to 40\to 20\to 10 \to 5 \to 16\to 8 \to 4 \to 2\to 1

となって， $13$ 回のステップで $1$ に到達する。

途中からは例1と同じ数字が出現しますね。

例3.

$a=27$ とすると，

\scriptsize 27\to 82\to 41\to 124\to 62\to 31\to 94\to 47\to 142\to 71\to 214\to 107\to 322\to 161\to 484\to 242\to 121\to 364\to 182\to 91\to 274\to 137\to 412\to 206\to 103\to 310\to 155\to 466\to 233\to 700\to 350\to 175\to 526\to 263\to 790\to 395\to 1186\to 593\to 1780\to 890\to 445\to 1336\to 668\to 334\to 167\to 502\to 251\to 754\to 377\to 1132\to 566\to 283\to 850\to 425\to 1276\to 638\to 319\to 958\to 479\to 1438\to 719\to 2158\to 1079\to 3238\to 1619\to 4858\to 2429\to 7288\to 3644\to 1822\to 911\to 2734\to 1367\to 4102\to 2051\to 6154\to 3077\to 9232\to 4616\to 2308\to 1154\to 577\to 1732\to 866\to 433\to 1300\to 650\to 325\to 976\to 488\to 244\to 122\to 61\to 184\to 92\to 46\to 23\to 70\to 35\to 106\to 53\to 160\to 80\to 40\to 20\to 10\to 5\to 16\to 8\to 4\to 2\to 1

となって， $111$ 回のステップで $1$ に到達する。

このように，一見27という単純な数からスタートしても，非常に多くの数を「経由」し，多くのステップがかかることがあります。コラッツ予想は複雑な問題なわけです。

多くの数において，ちゃんと有限回のステップで $1$ に到達することが，コンピューターを用いた数値計算によって確認されています。Wikipediaによると，初期値が $a = 2^{68}\approx 2.95 \times 10^{20}$ 程度までは確認されているようです。

正しいか正しくないかを明らかにするためには，任意の $a$ に対して成り立つことを証明するか，あるいは，逆にある $a$ に対して $1$ に到達しない「反例」を挙げねばなりません。上の数値計算は，反例がないかどうかを探索しているわけですね。

コラッツ予想は多額の懸賞金がかけられている

2021年7月7日，とある音楽系の日本企業が，コラッツ予想に1億2000万円の懸賞金をかけると発表しました。数学の未解決問題にかけられている懸賞金としては，「ミレニアム問題」と呼ばれる，複数の問題が有名ですが，これの懸賞金が1問あたり100万ドルです。これを超える額ですね。実際，史上最高額だそうです。夢がありますね。