統計学,統計的分類における「混同行列」や「真陽性・真陰性・偽陽性・偽陰性」といった概念を解説します。
とある測定機器の精度評価をする際には,欠かせない指標ですから,しっかり理解していきましょう。
混同行列と偽陽性・偽陰性をわかりやすく図解
ある事柄について,測定機器を用いて「陽性 (positive) 」か「陰性 (negative) 」か判断したいとしましょう。例えば,以下のような事柄です。
- ある人が病気に感染しているかどうか(感染していれば陽性)
- ある製造機器に傷やひび割れはないか(傷やひび割れがあれば陽性)
- あるメールが迷惑メールかどうか(迷惑メールであれば陽性)
今であれば,感染症について,陽性判断の検査をイメージするのが最も手っ取り早いでしょう。
このとき,測定機器の精度によって「実際に陽性かどうか」と「測定結果が陽性になるかどうか」の間にはズレが生じるのが普通です。
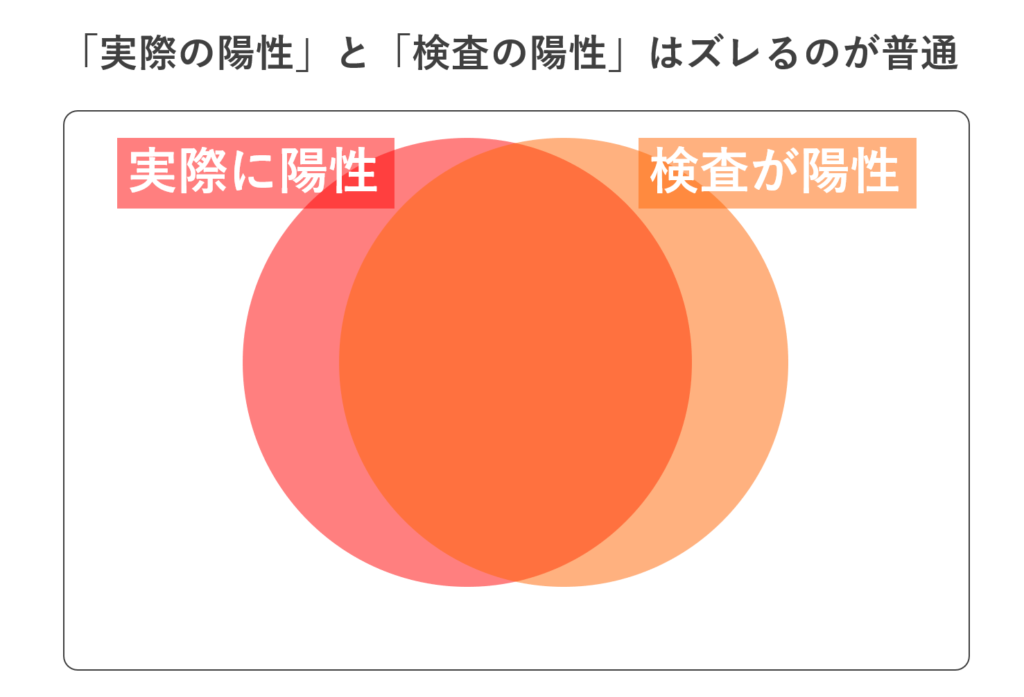
このとき,上の図は以下のように4つの領域に分けることができます。
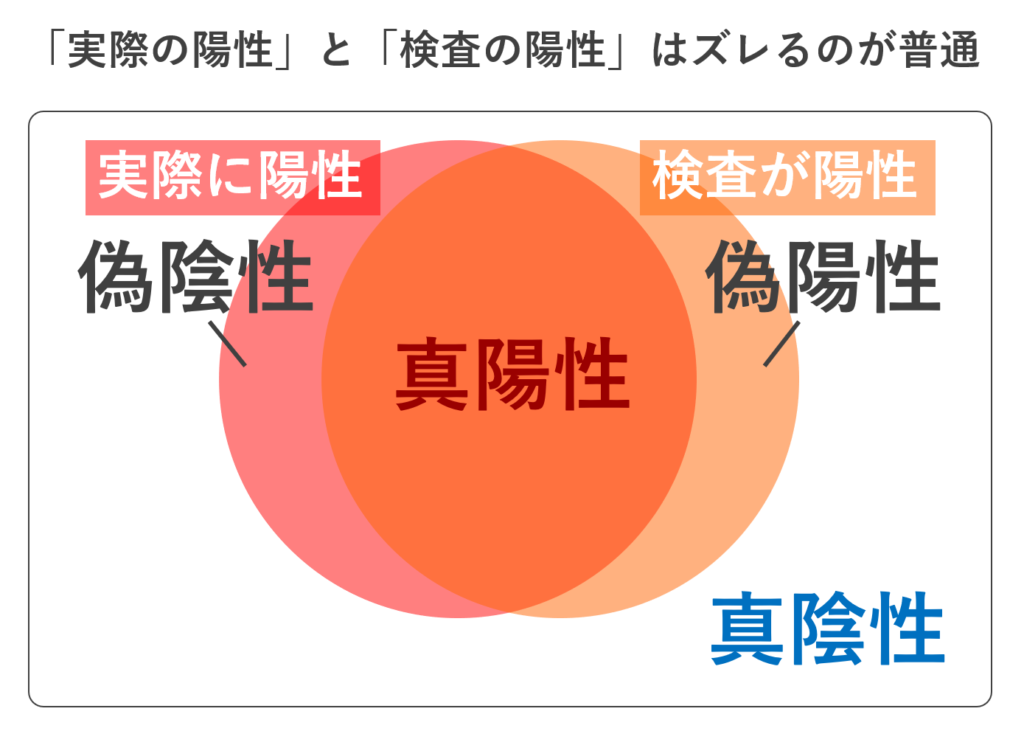
4つの領域
- 真陽性 (しんようせい; true positive) …… 正しく陽性と判断された
- 真陰性 (しんいんせい; true negative) …… 正しく陰性と判断された
- 偽陽性 (ぎようせい; false positive) …… 誤って陽性と判断された(本当は陰性)
- 偽陰性 (ぎいんせい; false negative) …… 誤って陰性と判断された(本当は陽性)
偽陽性は第一種の誤り,偽陰性は第二種の誤りとも言います。偽陽性は「過検出」で偽陰性は「検出漏れ」ですね。
これは,下のような 2\times 2 の行列にまとめることが可能です。
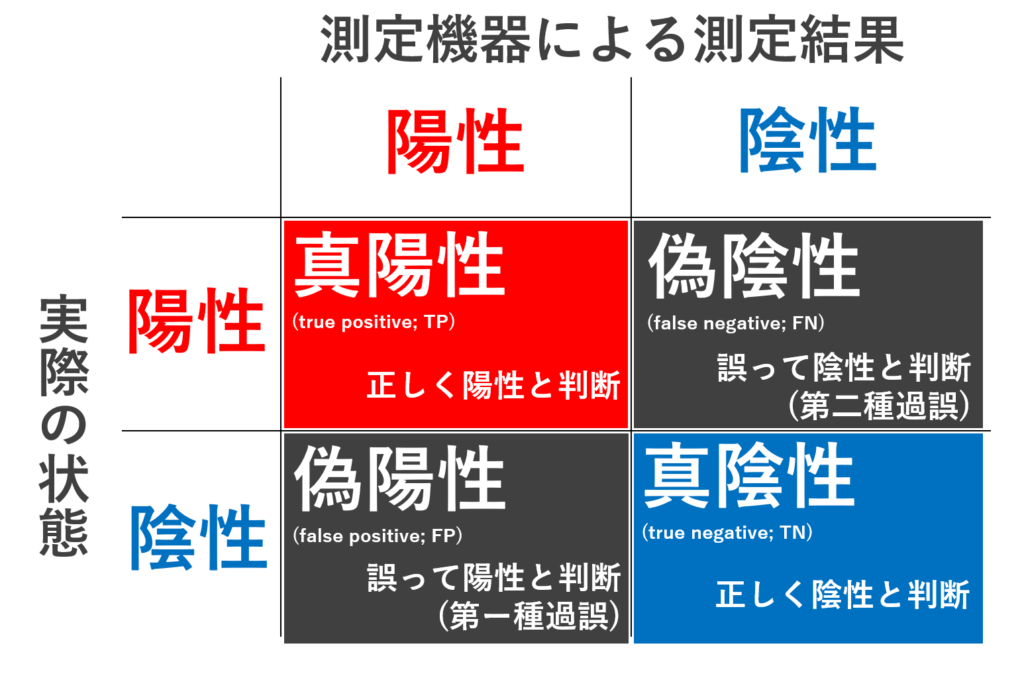
この行列を,混同行列 (confusion matrix) といいます。
具体例として,病気の陽性検査を考えてみましょう。それぞれの意味は以下のようになります。
- 真陽性 …… 実際に病気だし,検査でも陽性
- 真陰性 …… 実際に病気でないし,検査でも陰性
- 偽陽性 …… 実際は病気でないのに,検査では陽性が出てしまう(過検出)
- 偽陰性 …… 実際は病気なのに,検査では陰性になってしまう(検出漏れ)
実際の運用では,混同行列に人数や個数などの数量を当てはめます。以下のような感じです。
| 混同行列 | 検査が陽性 | 検査が陰性 |
|---|---|---|
| 実際に陽性 | 30人 | 7人 |
| 実際に陰性 | 4人 | 786人 |
行列として扱えますね。