凸集合とは簡単に言うと「へっこんでいない集合」のことをいいます。これについて,ちゃんとした定義と,性質を解説します。
凸集合とは
定義(凸集合)
C\subset \mathbb{R}^n が凸集合 (convex set) であるとは,
\color{red} \begin{aligned}&\boldsymbol{x_1},\boldsymbol{x_2}\in C\\&\implies (1-\theta)\boldsymbol{x_1}+\theta \boldsymbol{x_2} \in C \; (0\le\theta\le 1) \end{aligned}
が成り立つことを言う。
C\subset \mathbb{R}^n だけでなく,より一般に \mathbb{R} 上ベクトル空間 C\subset V で凸集合が定義できます。
(1-\theta)\boldsymbol{x_1}+\theta \boldsymbol{x_2} とは,点 \boldsymbol{x_1},\boldsymbol{x_2} を結んだ線分を \theta : (1-\theta) に内分する点を表します。
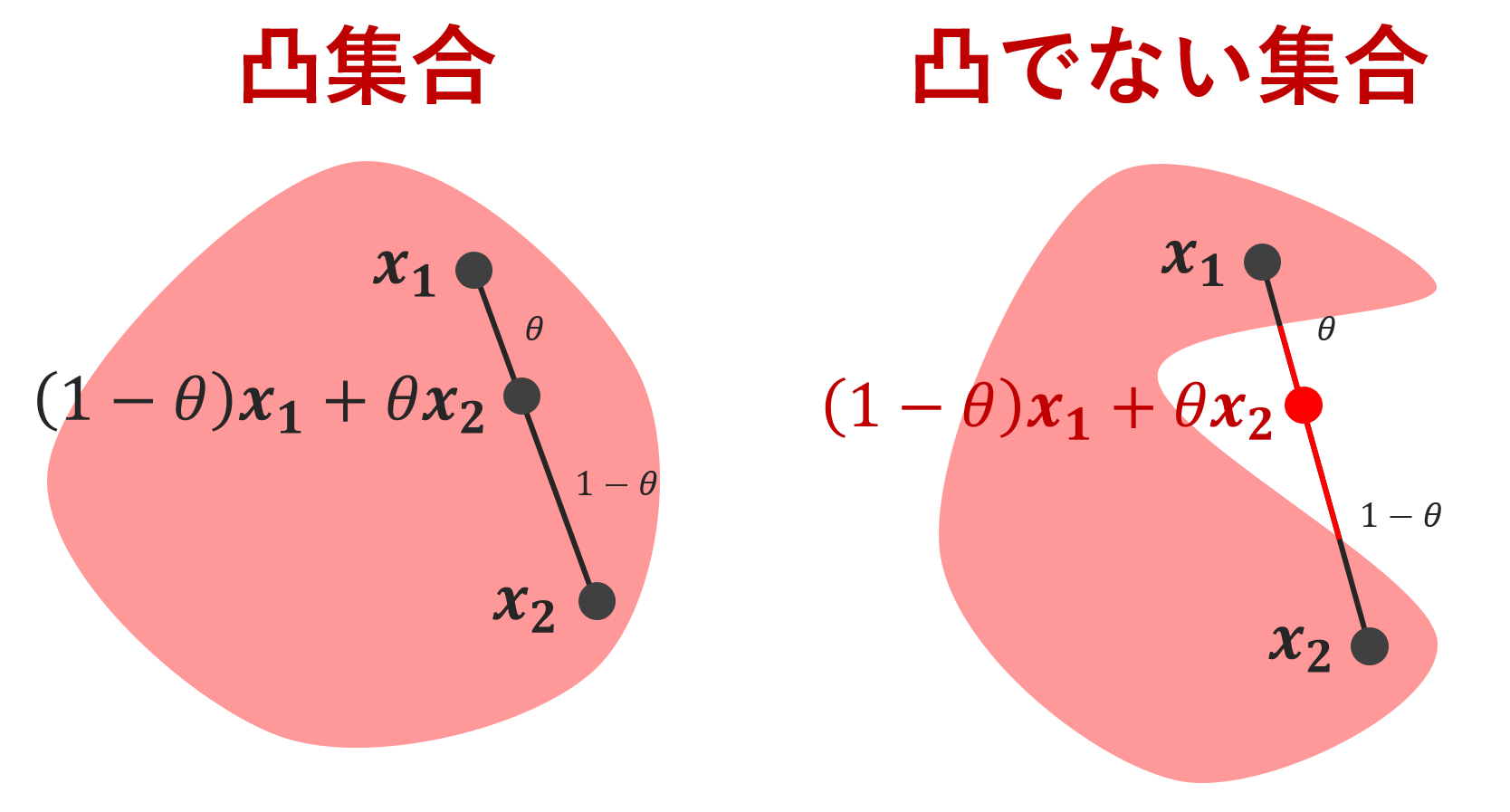
凸集合を簡単に言うと,へっこんでない集合です。以下の図を見てください。
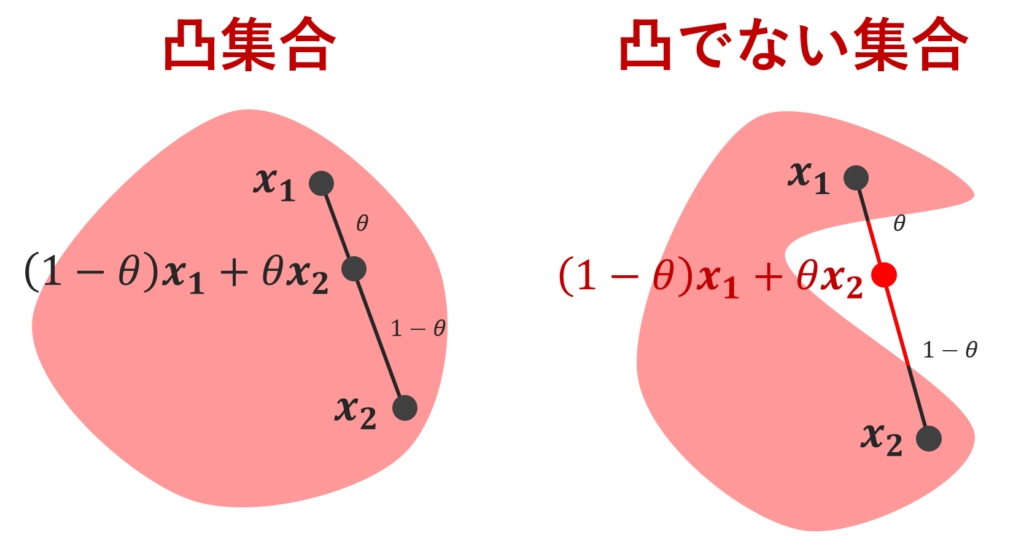
このように,集合 C 上の2点を線で結んだときに,その線が常に C からはみ出なければ凸集合で,はみ出るやつがある場合は凸集合ではありません。
たとえば, B =\{ (x_1, \dots, x_n)\in\mathbb{R}^n\mid x_1^2+ \dots +x_n^2\le 1\} や \mathbb{R}^n それ自体は凸集合の簡単な例です。
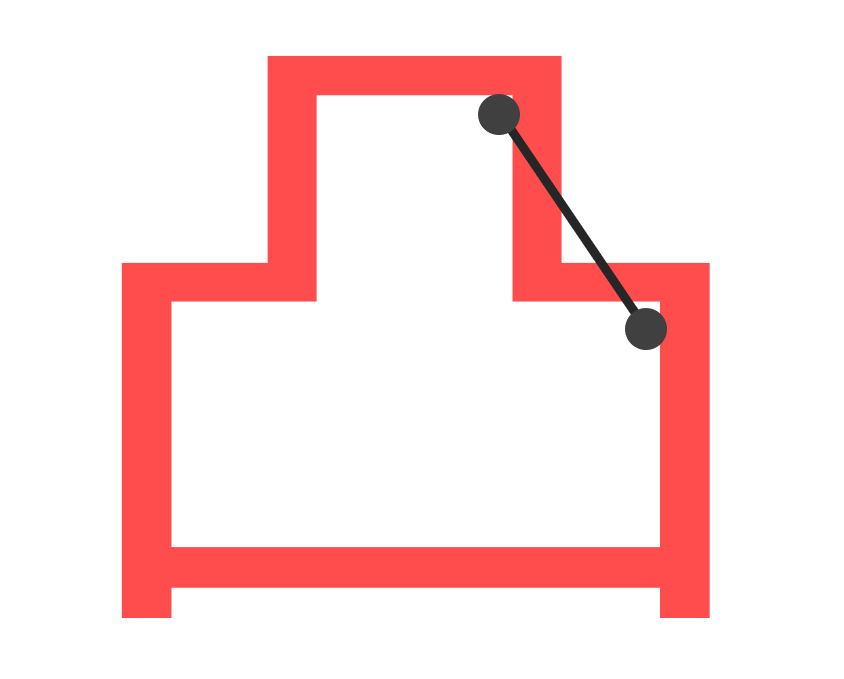
注意ですが,「凸(とつ)」という漢字は 2 次元集合として凸集合ではありません。線がはみ出していますね。
凸集合の性質
凸集合の簡単な性質を2つ挙げましょう。
定理(凸集合の性質)
- C\subset\mathbb{R}^n を凸集合とする( C\subset V, V は \mathbb{R} 上ベクトル空間でもよい)。このとき, \begin{aligned}&\!\!\!\boldsymbol{x_1}, \boldsymbol{x_2}, \dots, \boldsymbol{x_n}\in S \\ &\!\!\! \implies \sum_{k=1}^n \lambda_k \boldsymbol{x_k}\in S \; (\lambda_k\ge 0, \sum_{k=1}^n \lambda_k=1).\end{aligned}
- \{C_\lambda\}_{\lambda\in \Lambda} を凸集合の族とする。このとき, \bigcap_{\lambda \in \Lambda} C_\lambda も凸集合である。
証明しておきましょう。
証明
1.について
帰納法で示す。 n=2 のとき主張は明らか。 n-1 で主張が成立するとして, n でも成立することを述べる。
\overline{\lambda}_{n-1} = \lambda_1+\dots +\lambda_{n-1},\; \lambda'_k= \lambda_k/\overline{\lambda}_{n-1}\,(1\le k\le n-1) と定めると, \lambda'_1+\dots +\lambda'_{n-1}=1 である。よって帰納法の仮定より,\sum_{k=1}^{n-1} \lambda'_k \boldsymbol{x_k}\in C. この左辺を \boldsymbol{\overline{x}_{n-1}} とおくことにする。
ここで, 0\le \overline{\lambda}_{n-1}\le 1,\; \overline{\lambda}_{n-1}+\lambda_n =1,\; \overline{\lambda}_{n-1}\lambda'_k=\lambda_k \;(1\le k\le n-1) であることと, C は凸集合から,
\sum_{k=1}^n \lambda_k \boldsymbol{x_k}=\overline{\lambda}_{n-1}\boldsymbol{\overline{x}_{n-1}}+ \lambda_n \boldsymbol{x_n}\in C.
よって題意は示された。
2.について
\boldsymbol{x_1},\boldsymbol{x_2}\in \bigcap_{\lambda \in \Lambda} C_\lambda とする。これは,任意の \lambda\in \Lambda に対して, \boldsymbol{x_1},\boldsymbol{x_2}\in C_\lambda を意味する。
C_\lambda は凸集合なので,任意の \lambda \in \Lambda に対して, (1-\theta)\boldsymbol{x_1}+\theta\boldsymbol{x_2}\in C_\lambda となる。これは, (1-\theta)\boldsymbol{x_1}+\theta\boldsymbol{x_2} \in \bigcap_{\lambda \in\Lambda} C_\lambda を意味し, \bigcap_{\lambda\in\Lambda } C_\lambda が凸集合ということになる。
証明終
凸包
A\subset \mathbb{R}^n を含む最小の凸集合 C を凸包 (convex hull) といいます。これについては,以下で別途解説しています。