「カントールの対角線論法」あるいは単に「対角線論法」とは,数学における証明のテクニックの1つです。これについて,その内容を,実際の証明を通して理解していきましょう。
カントールの対角線論法とそれを用いた証明
カントールの対角線論法とは,証明の手法を指します。カントールの対角線論法を用いた定理で最も有名である,以下の定理を証明してみましょう。
実数の個数は自然数の個数よりも真に大きい
以下では, \mathbb{N}=\{1,2,3,\dots\} を自然数全体の集合とします。
定理(実数と自然数の濃度)
実数 \mathbb{R} と自然数 \mathbb{N} の間に全単射は存在しない。
すなわち,集合の濃度について,\color{red} |\mathbb{N}|<|\mathbb{R}| である。
早速証明を見ていきましょう。後で図解するため,大体の理解で良いです。
証明
\mathbb{R} と (0,1] の間には全単射があるから, f\colon \mathbb{N}\to (0,1] が全単射になり得ないことを示せばよい。
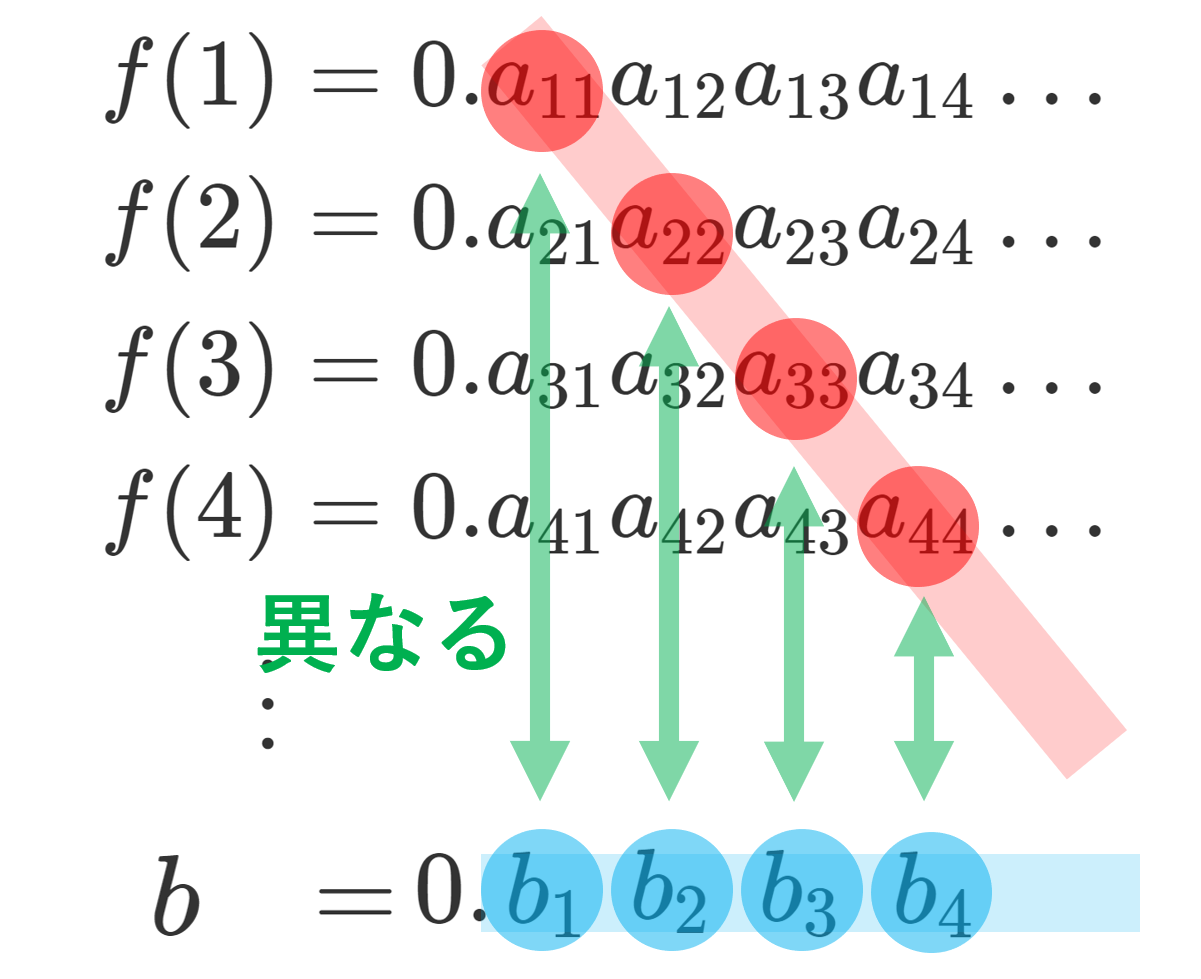
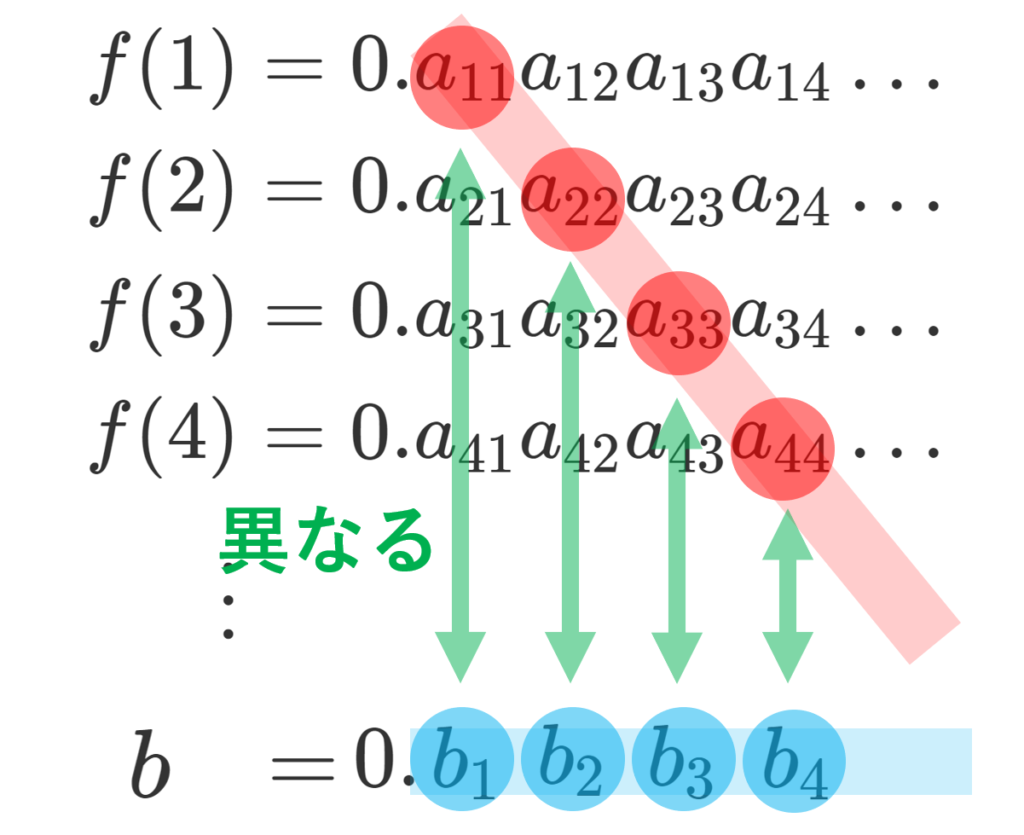
\begin{aligned} f(1) &= 0.a_{11}a_{12}a_{13}a_{14}\dots \\ f(2)&= 0.a_{21}a_{22}a_{23}a_{24}\dots \\ f(3)&= 0.a_{31}a_{32}a_{33}a_{34}\dots \\ f(4)&= 0.a_{41}a_{42}a_{43}a_{44}\dots \\ \vdots \end{aligned}
と小数表示する。ただし, 1=0.999\dots, \; 0.03=0.02999\dots のように,有限小数も無限小数で表すことにする。 ここで,各 n\ge 1 について,
と定める(evenは偶数,oddは奇数の意味)。すると,0.b_1b_2b_3b_4\dots \in (0,1] である。これを b と定めよう。
0.b_1b_2b_3b_4\dots は 0.0999\dots =0.1 のように2通りで表せることはなく,かつ任意の n に対して, a_{nn}\ne b_n であることから,任意の n に対して, f(n)\ne b である。
従って, b\notin f(\mathbb{N}) であるから,f は全射でない。
証明終
図解していきましょう。 f を例えば次のように定めたとしましょう。このとき, a_{kk} に着目して,同時に b=b_1b_2b_3b_4\dots の値も記述すると,以下のようになります。

このとき,次のように,対角線の成分と b の各桁を比較すると,その定義から必ず異なっていることが分かると思います。

これより, b は f(n) の形で表せないことになりますね。これは,f が全射でないことを意味しています。
このように,対角線を見て,その成分に注目しているような証明手法を,カントールの対角線論法 (Cantor’s diagonal argument) といいます。
なお,この論法は,具体的に対応関係を定めて b を構成しているため,選択公理は不要です(→選択公理の内容と具体例を詳しく)。
また,十進展開で進めましたが,二進展開で議論を進めても構いません。
【カントールの定理】べき集合の濃度は元の濃度より大きい
べき集合の濃度についての以下の定理も,カントールの対角線論法を用いる定理として有名です。
|A|<|2^A| とは,簡単に言うと全単射 f\colon A\to 2^A が存在しないことを示せばよいです。
A が有限集合のとき, n<2^n ですから,明らかです。無限集合のときにも考えられることが大切です。
証明
|A|\le |2^A| は, a\mapsto \{a\} が単射から従う。よって, f\colon A\to 2^A としたとき,これが全単射でないことを示せばよい。
B=\{ a\in A\mid a\notin f(a)\}
と定めると, B\in 2^A であるが, B\notin f(A) である。実際, B\in f(A) と仮定すると,ある a\in A が存在して, f(a)=B とできる。
- a\in B のとき,a\in B=f(a) だが B の定義に矛盾する。
- a\notin B のとき, B の定義より a\in f(a)=B であり,矛盾している。
よって,確かに B\notin f(A) なので,f は全射でない。
証明終
A のべき集合 2^A とは, A の部分集合の集合全体 \{B\mid B\subset A\} を指します。 2^A の各元は, A の各元を選ぶか選ばないかを決めることによって定まるので,これは写像の集合
2^A=\{ B\mid B\colon A\to \{0,1\} \}
と考えてもよいです。したがって,べき集合 2^A の元は,以下のように「 0,1 の数の列」で表現してもよいでしょう。 A の部分集合として含む元を 1 ,含まない元を 0 と表現しています。
上の図を表現している部分集合を例えば B\subset A\; (B\in 2^A) とすると, a_1\in B,\; a_2\notin B,\dots です。
まるで「二進展開」のようですね。このとき, a\notin f(a) をみたす 2^A の元は, a_1\notin f(a_1),\, a_2\notin f(a_2),\dots ですから,先ほどの二進展開の対角成分に注目し,0,1 を入れ替えたものになります。
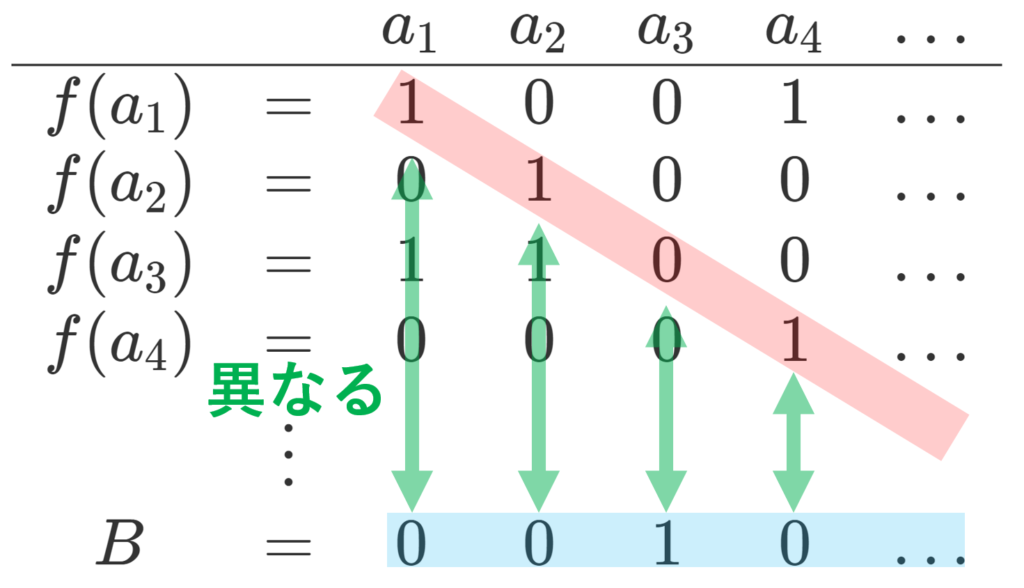
こう考えると,同じく「対角線論法」になっているのが分かるのではないでしょうか。これはあくまでイメージですが,このような,より一般的な話も「カントールの対角線論法」といいます。うまいテクニックですね。