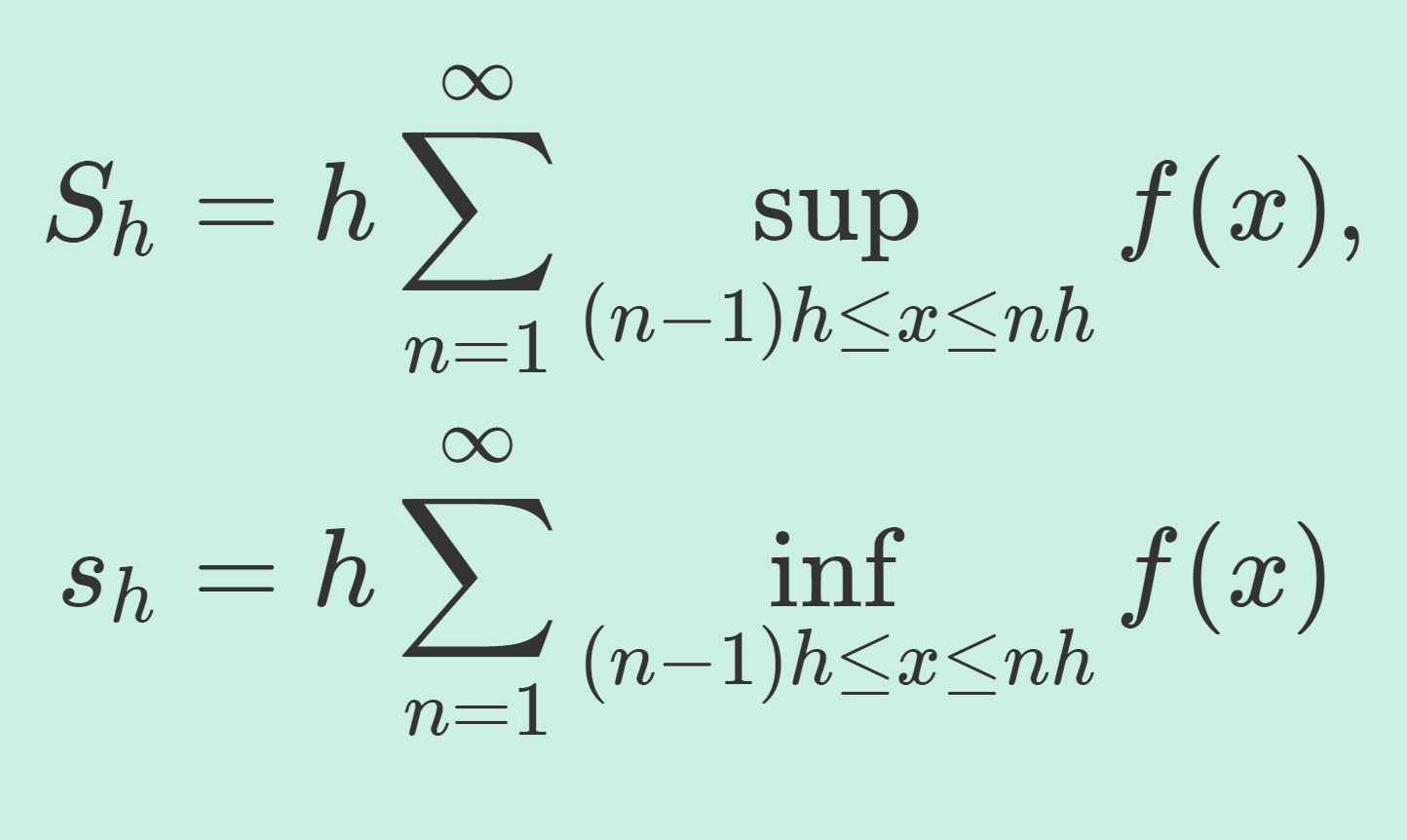Directly Riemann Integrableの定義と例

無限区間でリーマン和（区分求積）を考えることが可能である Directly Riemann Integrable (dRi) な関数について，その定義と例を紹介します。

Directly Riemann Integrableの定義

広義積分 (improper integral) は「区間が有界でない」ものと「関数がある点で有界でない」ものがありました。これらは，どちらにおいても，

有界な上でのリーマン和 → 有界な上でのリーマン積分 → リーマン積分を極限により拡張

の順番を辿って定義しました。

Directly Riemann Integral とは，「区間が有界でない」ものについて，最初から無限区間上でリーマン和を考えようというものです。もともとの広義積分において，リーマン和は有界区間上でしか考えていませんでしたが，そうではなく，直接リーマン和を考えているわけですね。

定義（Directly Riemann Integrable）

$f\colon [0,\infty)\to [0,\infty)$ を有界な関数とする。

\begin{aligned} S_h &=h \sum_{n=1}^\infty \sup_{(n-1)h\le x\le nh} f(x), \\ s_h &= h \sum_{n=1}^\infty \inf_{(n-1)h\le x\le nh} f(x) \end{aligned}

と定める。 $\lim_{h\to 0+} S_h = \lim_{h\to 0+} s_h<\infty$ のとき， $f$ は directly Riemann integrable (dRi)という。

無限区間上で区分求積を考えていますね。 $S_h$ が上からの近似で， $h\to 0+$ とすると単調減少し， $s_h$ は下からの近似で， $h\to 0+$ とすると単調増加します。

このとき，以下の定理は基本的です。

定理（dRiなら広義リーマン積分可能）

有界な関数 $f\colon [0,\infty)\to [0,\infty)$ が dRi であるとする。このとき， $\int_0^\infty f(x)\,dx$ (広義リーマン積分)は収束して，

\color{red}\lim_{h\to 0+} S_h = \lim_{h\to 0+} s_h = \int_0^\infty f(x)\,dx.

ただし， $S_h, s_h$ は dRi の定義中のものである。さらに，

\color{red}\lim_{x\to\infty } f(x) =0

も成立する。

dRi は広義積分可能より強い概念だということですね。

注意ですが，単に広義リーマン積分可能だけでは， $\lim_{x\to\infty } f(x) =0$ は言えません。たとえば， $f(x) = 1_{[n, n+ 1/n^2]} \; (n\ge 1)$ (定義関数) は広義積分可能ですが， $\lim_{x\to\infty } f(x) =0$ ではありませんね。特に，この関数は広義積分可能だが dRi でない例でもあります。

証明