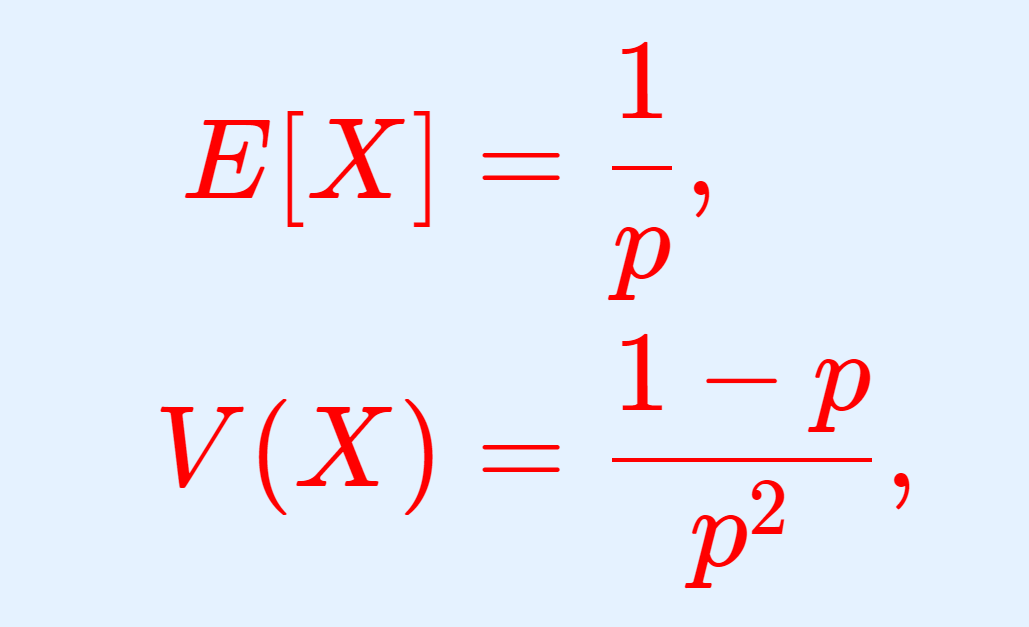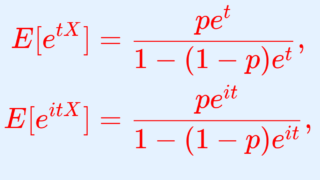幾何分布における期待値(平均)・分散・標準偏差は，それぞれ
\begin{aligned}E[X] &= \dfrac{1}{p}, \\ V(X)&= \dfrac{1-p}{p^2 }, \\ \sqrt{V(X)} &= \dfrac{\sqrt{1-p}}{p} \end{aligned}
です。これについて，深く掘り下げていきましょう。
幾何分布の期待値(平均)・分散・標準偏差
まずは，もう一度ちゃんと結論を述べましょう。
定理（幾何分布の期待値(平均)・分散・標準偏差）
X \sim \operatorname{Geo}(p) とする。このとき， X の期待値・分散・標準偏差はそれぞれ
\color{red} \begin{aligned}E[X] &= \dfrac{1}{p}, \\ V(X)&= \dfrac{1-p}{p^2 }, \\ \sqrt{V(X)} &= \dfrac{\sqrt{1-p}}{p} \end{aligned}
である。
さて，上の証明に行く前に，まず幾何分布の定義を復習しておきましょう。
X を確率変数， 0<p<1 とする。 k=1,2,3,\ldots に対し，
\color{red} P(X=k) = (1-p)^{k-1} p
が成立するとき， X はパラメータ p の幾何分布 (geometric distribution) に従うという。本記事では，これを \color{red} X\sim \operatorname{Geo}(p) とかくことにする。
幾何分布は，離散型確率分布の1つで，「確率 p で表が出るコインを何回も振ったときに，何回目に初めて表が出るか」をモデル化したものです。幾何分布について，詳しくは以下の記事を参照してください。
幾何分布の期待値(平均)の導出証明
期待値(平均)の導出について，
- 定義から直接証明する方法
- 特性関数の微分で証明する方法
の２通りで証明していきましょう。
【期待値】定義から直接証明する方法
まずは，定義を用いて，直接証明してみましょう。
証明
期待値と幾何分布の定義から，
\begin{aligned}E[X] &= \sum_{k=1}^\infty k P(X=k) \\ &= \sum_{k=1}^\infty k (1-p)^{k-1} p \\ &= p \sum_{k=1}^\infty k (1-p)^{k-1}. \end{aligned}
ここで，m= \sum_{k=1}^\infty k (1-p)^{k-1} とおこう。
\small \begin{alignedat}{4} m &= &1& + &2(1-p)&+ &3(1-p)^2& +\cdots, \\ (1-p)m&= && &(1-p)&+ &2(1-p)^2& +\cdots \\ \end{alignedat}
であるから，辺々引くと
pm = 1 + (1-p) + (1-p)^2 + \cdots
なので，
\begin{aligned} pm &=\sum_{k=0}^\infty (1-p)^k = \frac{1}{1-(1-p)}= \frac{1}{p} \end{aligned}
であるから， m = 1/p^2 . したがって，
E[X] = p\sum_{k=1}^\infty k (1-p)^{k-1} = pm = \frac{1}{p}.
証明終
「等差 × 等比 級数」の形になって，証明することができましたね。
【期待値】特性関数の微分で証明する方法
さて，次は特性関数の微分を用いて証明してみましょう。まずは，特性関数がどうなるかを確認します。
\color{red} E[e^{itX}]= \dfrac{pe^{it}}{1-(1-p)e^{it}}, \quad t\in\mathbb{R}
これの導出は，以下の記事で行っています。
これを用いて，期待値の導出をしてみましょう。
証明
特性関数の上の等式を t で微分すると，
E[iXe^{itX}] = \frac{ipe^{it}}{(1-(1-p)e^{it})^2}
であるから，両辺 t= 0 を代入して， E[iX] = \dfrac{i}{p} なので，
E[X] =\frac{1}{p}.
証明終
なお，今回は「特性関数」を微分しましたが，「積率母関数(モーメント母関数)」を微分しても同様に得ることができます。
幾何分布の分散の導出証明
分散は， V(X) = E[x^2]-E[X]^2 を使って求めましょう。こちらも，
- 定義から直接証明する方法
- 特性関数の微分で証明する方法
の２通りで証明していきましょう。
【分散】定義から直接証明する方法
さて，まずは直接証明する方法を行いましょう。
証明
まずは2次モーメント E[X^2] を求めよう。
\begin{aligned}E[X^2] &= \sum_{k=1}^\infty k^2 P(X=k) \\ &= \sum_{k=1}^\infty k^2 (1-p)^{k-1} p \\ &= p \sum_{k=1}^\infty k^2 (1-p)^{k-1} \end{aligned}
であるから， s = \sum_{k=1}^\infty k^2 (1-p)^{k-1} とおく。
\small \begin{alignedat}{4} s&= &1^2& + &2^2(1-p)& + &3^2(1-p)^2& + \cdots,\\ (1-p)s&= && + &1^2 (1-p) & + &2^2 (1-p)^2 & \cdots \end{alignedat}
であるから，辺々引いて， k^2-(k-1)^2 = 2k-1 から
\begin{aligned} ps &= 1 + 3(1-p) + 5(1-p)^2 +\cdots \\ &=\sum_{k=1}^\infty (2k-1)(1-p)^{k-1} \\ &= 2m - \sum_{k=1}^\infty (1-p)^{k-1} \\ &= \frac{2}{p^2} - \frac{1}{p} \end{aligned}
がわかる。ただし，m= \sum_{k=1}^\infty k (1-p)^{k-1} は期待値の導出のときに計算したものである。これより， E[X^2] = ps = (2-p)/p^2 である。以上から，
\begin{aligned} V(X)=E[X^2] - E[X]^2 &= \frac{2-p}{p^2} - \frac{1}{p^2} \\ &= \frac{1-p}{p^2}. \end{aligned}
証明終
【分散】特性関数の微分で証明する方法
さて，期待値のときと同じく，分散も特性関数を用いて求めましょう。
証明
特性関数の式 E[e^{itX}]= \dfrac{pe^{it}}{1-(1-p)e^{it}} を t で二回微分して
E[(iX)^2e^{itX}] = -\frac{pe^{it}(1+(1-p)e^{it})}{(1-(1-p)e^{it})^3}.
t=0 を代入すると，
E[X^2] = \frac{2-p}{p^2}.
よって，
\begin{aligned} V(X)=E[X^2] - E[X]^2 &= \frac{2-p}{p^2} - \frac{1}{p^2} \\ &= \frac{1-p}{p^2}. \end{aligned}
証明終
幾何分布の標準偏差について
標準偏差は，分散の平方根 \sqrt{V(X)} でしたから，上で V(X) = \dfrac{1-p}{p^2} と求めたことから，
\sqrt{V(X)} = \frac{\sqrt{1-p}}{p}
ですね。
