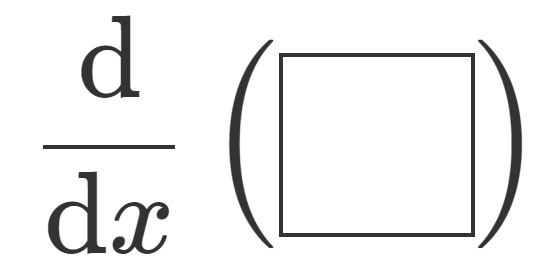【LaTeX】微分・偏微分のさまざまなかき方まとめ

\LaTeX における，微分・偏微分のさまざまなかき方（プライム・ドット・微分作用素d・偏微分作用素∂・ナブラ∇・ラプラシアン∆など）をまとめましょう。

なお，amsmath パッケージの使用を暗に仮定しているところがあります。

【LaTeX】微分のさまざまなかき方まとめ

まずは微分のかき方について，プライム・ドットを用いる方法と，微分作用素（分数表記）のものを別々にまとめましょう。

プライム(ダッシュ)・ドットを用いた微分

記号	コマンド
f'(x)	f'(x)
f^{\prime}(x)	f^{\prime}(x)
f^{\prime\prime\prime}(x)	f^{\prime\prime\prime}(x)
f^{(n)}(x)	f^{(n)}(x)
\dot{a}	\dot{a}
\ddot{a}	\ddot{a}
	\dddot{a}
	\ddddot{a}

' でプライムを表すときは，^ は不要です。' 記号は，重ねることのできる回数に上限があることがあるため，その場合は \prime を用いるとよいです。

日本では「ダッシュ」と呼ばれることもありますが，ダッシュは \text{---} のような単なる横線を指すのが正確です。(→ 【LaTeX】ハイフン,en,emダッシュ(横棒)とその使い分け)

微分作用素dを用いた微分

physics パッケージを用いると，微分は簡単にかけます。これを用いる場合と用いない場合，それぞれのコマンドを併記しましょう。

記号	コマンド	physicsパッケージ
d/dx	d/dx	\dv*{x}
df/dx	df/dx	\dv*{f}{x}
\dfrac{d}{dx}	\frac{d}{dx}	\dv{x}
\dfrac{df}{dx}	\frac{df}{dx}	\dv{f}{x}
\dfrac{d^nf}{dx^n}	\frac{d^nf}{dx^n}	\dv[n]{f}{x}
\dfrac{d}{dx}\left(\boxed{\phantom{hg}}\right)	\frac{d}{dx}\left(...\right)	\dv{x}(...)
\mathrm{d}/\mathrm{d}x	\mathrm{d}/\mathrm{d}x	\dv*{x}
\mathrm{d}f/\mathrm{d}x	\mathrm{d}f/\mathrm{d}x	\dv*{f}{x}
\dfrac{\mathrm{d}}{\mathrm{d}x}	\frac{\mathrm{d}}{\mathrm{d}x}	\dv{x}
\dfrac{\mathrm{d}f}{\mathrm{d}x}	\frac{\mathrm{d}f}{\mathrm{d}x}	\dv{f}{x}
\dfrac{\mathrm{d}^nf}{\mathrm{d}x^n}	\frac{\mathrm{d}^nf}{\mathrm{d}x^n}	\dv[n]{f}{x}
\dfrac{\mathrm{d}}{\mathrm{d}x}\left(\boxed{\phantom{hg}}\right)	\frac{\mathrm{d}}{\mathrm{d}x}\left(...\right)	\dv{x}(...)

微分作用素は d のようにイタリックにする場合と， \mathrm{d} のようにローマン体にする場合があります。ローマン体にするときは，通常 \mathrm{d} のようにします。

微分作用を立ててかくには，通常分数のコマンド \frac{}{} を用います。分数のかき方のテクニックは，【LaTeX】分数のかき方とテクニックも参照してください。

physicsパッケージの場合は，デフォルトではローマン体 \mathrm{d} で出力されます。もし， d のようなイタリック体にしたい場合は，\usepackage[italicdiff]{physics} のように読み込みます。

\dfrac{d}{dx}\left(\boxed{\phantom{hg}}\right), \dfrac{\mathrm{d}}{\mathrm{d}x}\left(\boxed{\phantom{hg}}\right) に関しては，普通のコマンドの方は括弧の大きさを自動調整する \left, \right を用いました。括弧のかき方については【LaTeX】括弧類のかき方一覧と大きさの変更方法まとめも参考にしてください。また，physicsパッケージの場合は，括弧のコマンド \qty と同じ形式で，括弧の種類・大きさを自動調整することが可能です。\qty の形式についても，【LaTeX】括弧類のかき方一覧と大きさの変更方法まとめを参照してください。

また，代入する値を入れたい場合は，\left.\frac{df}{dx}\right|_{x=1} とすれば， \left.\dfrac{df}{dx}\right|_{x=1} のようになります。\left. \right| のようにすることで，右側にタテの棒のみを出力することが可能です。

【LaTeX】偏微分のさまざまなかき方まとめ

続いて，偏微分のかき方をまとめましょう。

添え字を用いた偏微分

記号	コマンド
f_x	f_x
f_{xy}	f_{xy}
\partial_x f	\partial_x f

\partial は \partial で出力します。

偏微分作用素∂を用いた偏微分

記号	コマンド	physicsパッケージ
\partial/\partial x	\partial/\partial x	\pdv*{x}
\partial f/\partial x	\partial f/\partial x	\pdv*{f}{x}
\dfrac{\partial}{\partial x}	\frac{\partial}{\partial x}	\pdv{x}
\dfrac{\partial f}{\partial x}	\frac{\partial f}{\partial x}	\pdv{f}{x}
\dfrac{\partial^n f}{\partial x^n}	\frac{\partial^n f}{\partial x^n}	\pdv[n]{f}{x}
\dfrac{\partial^2}{\partial x\partial y}	\frac{\partial^2}{\partial x\partial y}	\pdv{}{x}{y}
\dfrac{\partial^2 f}{\partial x\partial y}	\frac{\partial^2 f}{\partial x\partial y}	\pdv{f}{x}{y}
\dfrac{\partial}{\partial x}\left(\boxed{\phantom{hg}}\right)	\frac{\partial}{\partial x}\left(...\right)	\pdv{x}(...)

微分作用素のときとほぼ同じです。

ベクトルと微分(ナブラ∇,ラプラシアン∆)

記号	コマンド	physicsパッケージ
\nabla	\nabla
\boldsymbol{\nabla}	\bm{\nabla} \usepackage{bm} が必要	\grad
\nabla^2	\nabla^2	\laplacian
\Delta	\Delta
\varDelta	\varDelta
\vec{\nabla}	\vec{\nabla}
\bm{\vec{\nabla}}	\bm{\vec{\nabla}} \usepackage{bm} が必要	\grad \usepackage[arrowdel]{physics} とした場合

\laplacian に関しては，\qty と同じ形式で，後ろに大きさが自動調整できる括弧をつけることができます。\qty の形式については，【LaTeX】括弧類のかき方一覧と大きさの変更方法まとめを参照してください。

【LaTeX】汎関数微分

physicsパッケージを用いた場合，汎関数微分に関するコマンドもあります。簡単に紹介しておきましょう。

コマンド	physicsパッケージ
\delta F[g(x)]	\var{f[g(x)]}
\delta(E-TS)	\var(E-TS)
\delta/\delta g	\fdv*{g}
\delta F/\delta g	\fdv*{F}{g}
\dfrac{\delta}{\delta g}	\fdv{g}
\dfrac{\delta F}{\delta g}	\fdv{F}{g}
\dfrac{\delta}{\delta V}(E-TS)	\fdv{V}(E-TS)

関連する記事

• 【LaTeX】積分,重積分,周回積分のコマンドとテクニック
• 【LaTeX】和をあらわすΣ(シグマ)記号のかき方とテクニック

参考

1. physics – Macros supporting the Mathematics of Physics