近傍・近傍系と基本近傍系～定義・具体例から位相を定めるまで～

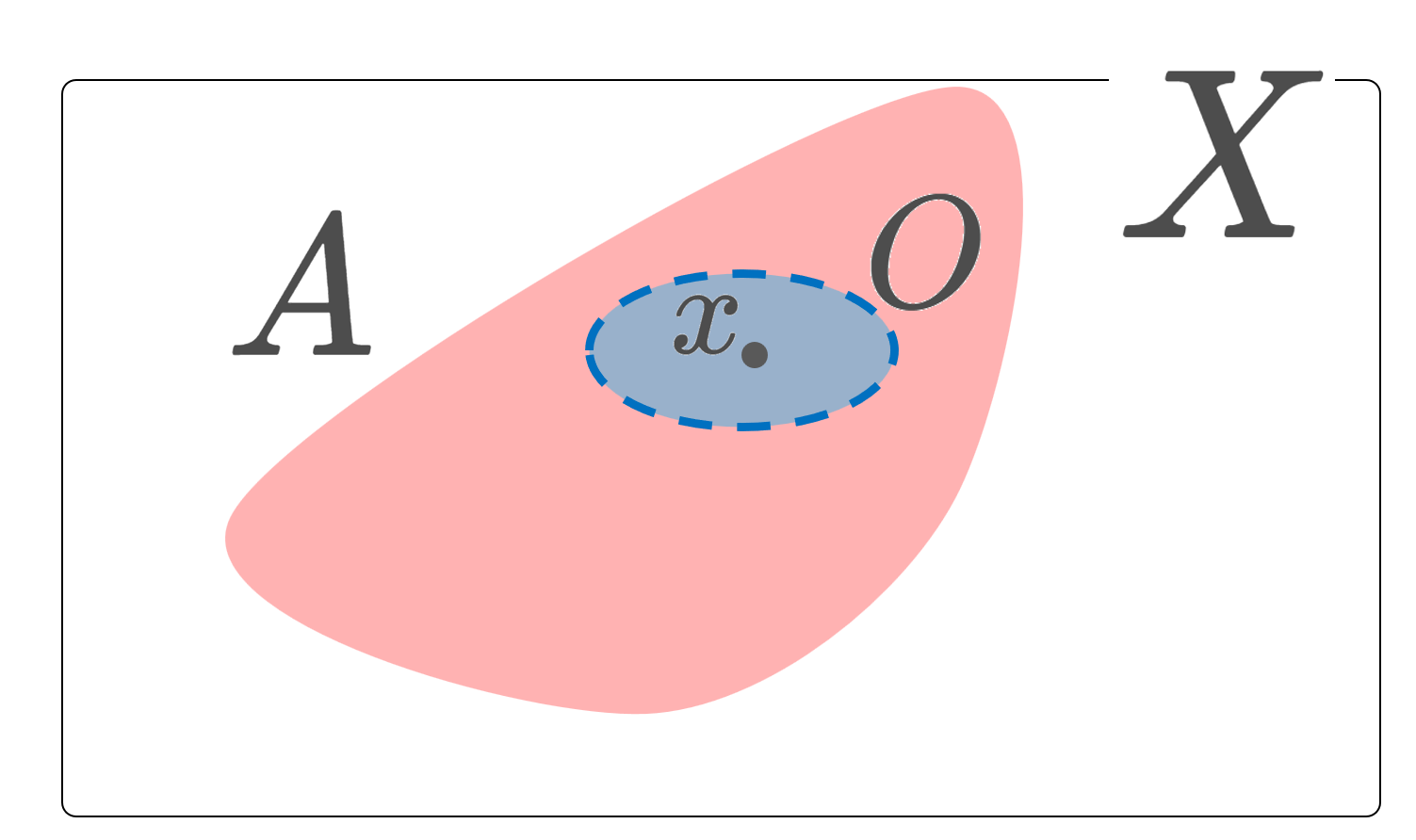
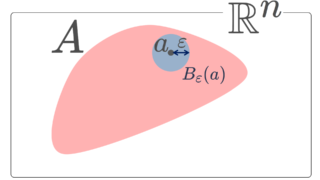
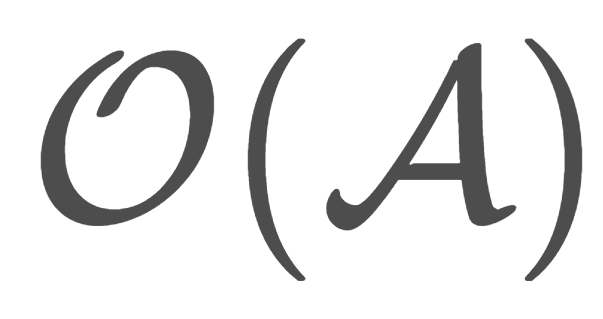一般の位相空間における近傍とは，距離のない位相空間に，ある意味「近さ」の概念を入れるものです。距離空間における $\varepsilon$ -近傍から出発して，それを一般化する形で定義します。さらに，基本近傍系はすべての近傍を記述するのに必要十分な部分集合族です。

近傍・近傍系と基本近傍系の定義からはじめ，逆に近傍系を用いて位相を定義する話まで解説しましょう。

近傍・近傍系の定義と具体例
1. 距離空間における近傍
2. 位相空間における近傍・近傍系
近傍・近傍系の性質
1. 近傍系から位相を定める
基本近傍系の定義と具体例
基本近傍系の性質
1. 基本近傍系から位相を定める
発展した概念
関連する記事
参考

近傍・近傍系の定義と具体例

まず距離空間における近傍を定義し，それから位相空間における近傍を定義します。

距離空間における近傍

距離空間 $(X,d)$ における近傍を定義しましょう。ユークリッド空間でも同じです。 $x\in X$ に対し， $x$ の $\varepsilon$ -近傍を

B_\varepsilon (x)= \{ y\in X\mid d(x,y)<\varepsilon \}

とします。

定義1（距離空間における近傍）

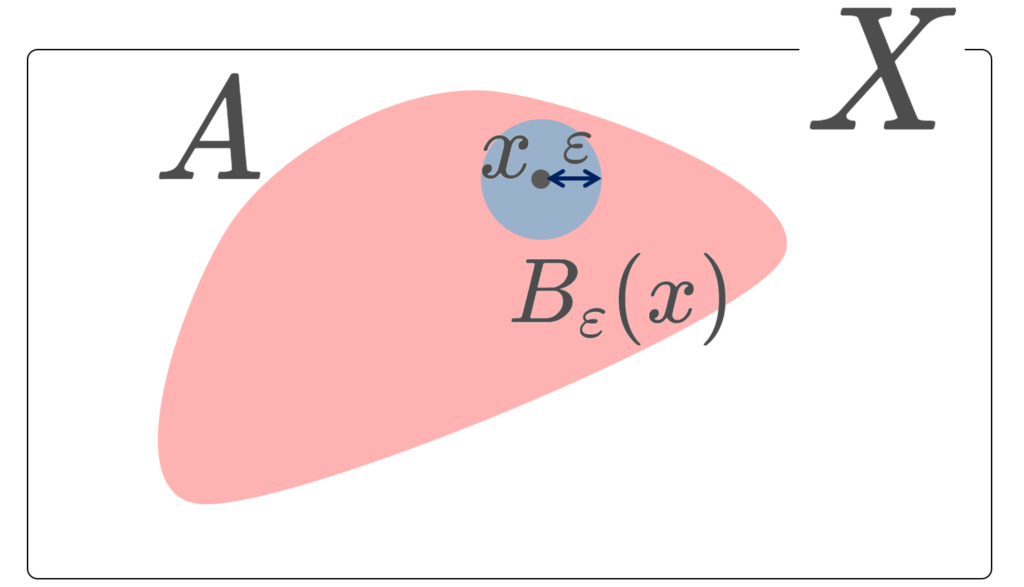
$(X, d)$ を距離空間とし， $x\in X$ とする。 $A\subset X$ が $x$ の近傍 (neighborhood) であるとは，ある $\varepsilon>0$ が存在して，

\color{red}\Large x\in B_\varepsilon (x)\subset A

が成り立つことをいう。

定義において， $x\in B_\varepsilon (x)$ の部分は当たり前なので不要です。分かりやすいかなと思ってつけています。

定義から明らかに $\varepsilon$ -近傍 $B_\varepsilon(x)$ 自体は $x$ の近傍です。また， $X$ 自身も $x$ の近傍ですが，あまり大きな近傍には興味がなく，小さい近傍が重要です。 $\varepsilon$ -近傍も $\varepsilon >0$ を小さくすることに意味があります。

$x$ の近傍とはただ単に「近い」というのではなく， $x$ の十分小さな周りを含んでいないといけないわけです。例を見ましょう。

近傍の例1.

数直線 $\R$ 上の点 $x\in \R$ に対し，

$a<x<b$ となる $a,b\in \R$ に対し， $(a,b), [a,b], (a,\infty), (-\infty, b]$ は $x$ の近傍である
$[x, x+1]$ や $[x-1, x]$ や $[x,\infty)$ は $x$ の近傍ではない

$x$ が区間の内部(開核)に含まれるようなときは，その区間は近傍です。一方， $x$ が区間の境界にあると，その区間は近傍とは言えません。

位相空間における近傍・近傍系

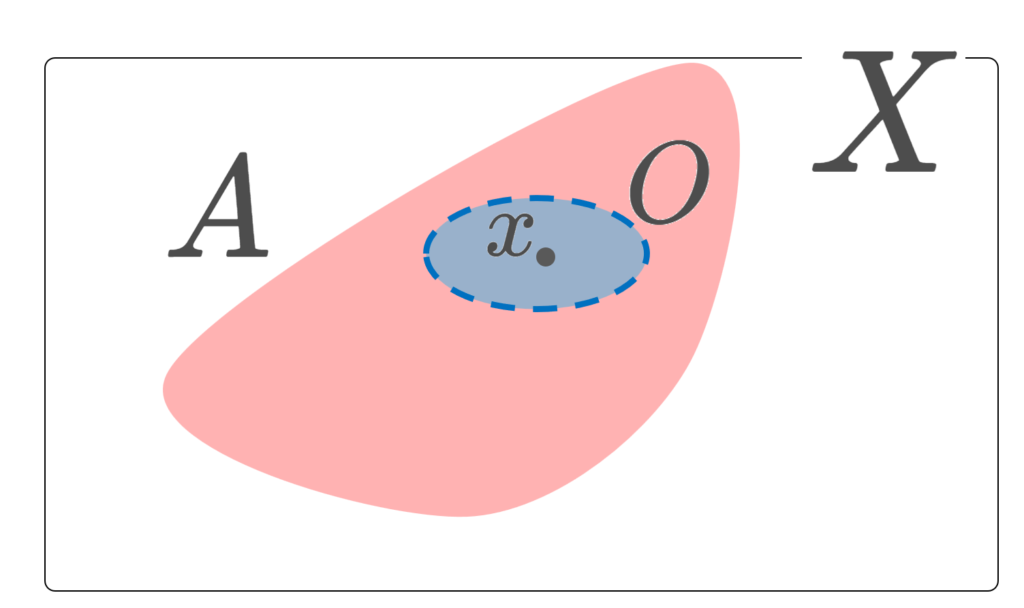
さてここからが本題です。距離空間における近傍の概念を，一般の位相空間に拡張しましょう。 $x\in X$ に対し， $A$ が $x$ の近傍 (neighborhood) であるとは，

\color{red} \Large x\in O\subset A

となる開集合 $O$ が存在することをいいます。ただし，結局これは $x\in \operatorname{Int}(A)$ というのと同じことです。ここで， $\operatorname{Int}(A)$ は $A$ の内部(開核)，すなわち $A$ に含まれる最大の開集合を表します。

定義2（位相空間における近傍・近傍系）

$(X,\mathcal{O})$ を位相空間とし， $x\in X$ とする。 $A\subset X$ が

\Large \color{red} x\in \operatorname{Int}(A)

をみたすとき， $A$ は $x$ の近傍 (neighborhood) であるという。ただし， $\operatorname{Int}(A)$ は $A$ の内部(開核)をあらわす。

定義より， $O$ が開集合であるとき， $x\in O$ ならば $O$ は $x$ の近傍である。このような $O$ を $x$ の開近傍 (open neighborhood) であるという。

$x\in X$ の近傍全体の集合 $\mathcal{N}(x)\subset 2^X$ を近傍系 (neighborhood system) という。ただし， $2^X$ は $X$ のべき集合をあらわす。

定義から明らかに $X$ は任意の点 $x\in X$ の開近傍といえますが，あまり大きな近傍には意味がなく，どちらかというと小さい近傍に興味があります。

近傍により，距離の定義されていない位相空間になんとなく「近さ」の概念が入ったようなイメージです。ただ，距離空間で定義したときと同じで， $x$ の近傍とはただ単に「近い」というのではなく， $x$ の十分小さな周りを含んでいると考えます。

近傍の例2(密着空間).

$(X, \{\emptyset, X\})$ を空でない密着空間とする。このとき， $x\in X$ の近傍は $X$ に限る。すなわち，

\mathcal{N}(x)=\{X\}

である。

密着空間は位相的な構造が不足しており，全ての点が「密着」しているような空間です。よって，近傍は全体集合しかありません。

近傍の例3(離散空間).

$(X, 2^X)$ を空でない離散空間とする。このとき， $x\in X$ に対し，

\mathcal{N}(x)=\{ N\subset X\mid x\in N\}

である。

$x$ を含むすべての部分集合が， $x$ の近傍になります。

近傍の例4.

2元以上の集合 $X$ について， $x\in X$ をとる。開集合系 $\mathcal{O}_x$ を

\mathcal{O}_x=\{\emptyset\} \cup \{O\subset X\mid x\in O\}

とすると， $(X,\mathcal{O}_x)$ は位相空間である。このとき，

\mathcal{N}(x) = \{ N\subset X\mid x\in N\}

であり， $y\in X\setminus \{x\}$ に対し，

\mathcal{N}(y) = \{ N\subset X\mid x, y\in N\}

である。

上の $\mathcal{N}(x)$ は $x$ を含む部分集合全体で， $\mathcal{N}(y)$ は $x$ と $y$ の両方を含む部分集合全体です。

近傍・近傍系の性質

定理1（近傍・近傍系の性質）

位相空間 $(X,\mathcal{O})$ の各点 $x\in X$ における近傍系 $\mathcal{N}(x)$ について，以下が成り立つ。

すべての $x\in X$ について， $X\in\mathcal{N}(x)$
$N\in\mathcal{N}(x)$ ならば $x\in N$
$N\in \mathcal{N}(x)$ かつ $N\subset N'$ ならば $N'\in\mathcal{N}(x)$
$N_1, N_2\in \mathcal{N}(x)$ ならば $N_1\cap N_2\in\mathcal{N}(x)$
任意の $N\in \mathcal{N}(x)$ について，ある $M\in\mathcal{N}(x)$ が存在して，
$y\in M\implies N\in \mathcal{N}(y)$
とできる。

1.から3.は明らかだと思うので，4.と5.を証明しましょう。

4, 5.の証明

4.について，仮定より， $x\in \operatorname{Int}(N_1), \, x\in \operatorname{Int}(N_2)$ であるから，

x\in \operatorname{Int}(N_1)\cap \operatorname{Int}(N_2)

である。 $\operatorname{Int}(N_1)\cap \operatorname{Int}(N_2) = \operatorname{Int}(N_1\cap N_2)$ であるから(→内部(開核)・外部・境界について詳しく図解～距離空間・位相空間～)， $x\in \operatorname{Int}(N_1\cap N_2)$ なので， $N_1\cap N_2\in \mathcal{N}(x)$ である。

5.については， $M= \operatorname{Int}(N)$ とすればよい

証明終

どれも当たり前の性質と思えるかもしれませんが，逆にこの性質があれば，近傍系が $\mathcal{N}(x)$ となる位相空間が定義できるという性質があるため，この5つの性質が大事になっています。

近傍系から位相を定める

定理2（近傍系から位相を定める）

$X$ を空でない集合とし，各 $x\in X$ に対し，集合族 $\mathcal{N}(x)\subset 2^X$ が定まっているとする。 $\mathcal{N}(x)$ が以下の条件をみたすとする(定理1の1.～5.と同じ)。

すべての $x\in X$ について， $X\in\mathcal{N}(x)$
$N\in\mathcal{N}(x)$ ならば $x\in N$
$N\in \mathcal{N}(x)$ かつ $N\subset N'$ ならば $N'\in\mathcal{N}(x)$
$N_1, N_2\in \mathcal{N}(x)$ ならば $N_1\cap N_2\in\mathcal{N}(x)$
任意の $N\in \mathcal{N}(x)$ について，ある $M\in\mathcal{N}(x)$ が存在して，
$y\in M\implies N\in \mathcal{N}(y)$
とできる。

このとき，ある開集合系 $\mathcal{O}$ から定まる位相空間 $(X,\mathcal{O})$ がただ一つ存在して， $N(x)$ を近傍系にすることができる。

証明は少々複雑です。

証明

開集合系 $\mathcal{O}$ を

\mathcal{O}=\{ O \subset X\mid \forall x\in O, \, O\in \mathcal{N}(x)\}

と定める。実際，近傍系の定義から， $\forall x\in O, \, O\in \mathcal{N}(x)$ をみたす $O$ は全て開集合でなければならないし，これをみたさない集合は開集合ではないから， $\mathcal{O}$ は存在すれば，上の定め方しかなく， $\mathcal{O}$ の一意性を表している。

まず， $\mathcal{O}$ が開集合系による位相空間の定義を満たしていることを示そう。

$\mathcal{O}$ の定義から明らかに $\emptyset \in \mathcal{O}$ であり，また，1.より $X\in \mathcal{O}$ である。

次に， $O_1, O_2\in \mathcal{O}$ とし， $x\in O_1\cap O_2$ とする。 $x\in O_1$ と $\mathcal{O}$ の定義より $O_1\in \mathcal{N}(x)$ であり，同様に $O_2\in\mathcal{N}(x)$ なので，4.より $O_1\cap O_2\in \mathcal{N}(x)$ となる。ゆえに $O_1\cap O_2\in\mathcal{O}$ である。

さらに， $\{ O_\lambda\}\subset \mathcal{O}$ とし， $O=\bigcup_{\lambda} O_\lambda,\, x\in O$ とする。このとき，ある $\lambda$ が存在して， $x\in O_\lambda$ なので， $O_\lambda\in \mathcal{N}(x)$ である。 $O_\lambda\subset O$ と3.より， $O\in \mathcal{N}(x)$ となる。ゆえに， $O\in \mathcal{O}$ である。

以上から， $\mathcal{O}$ は位相空間の定義をみたす。最後に， $\mathcal{N}(x)$ が位相空間 $(X,\mathcal{O})$ の近傍系 $\mathcal{V}(x)$ に一致していることを示そう。

まず， $V\in \mathcal{V}(x)$ とする。近傍系の定義より， $x\in \operatorname{Int}(V)$ である。このことと， $\operatorname{Int}(V)\in \mathcal{O}$ と $\mathcal{O}$ の定義より， $\operatorname{Int}(V)\in \mathcal{N}(x)$ である。3.より， $V\in \mathcal{N}(x)$ となるから， $\mathcal{V}(x)\subset \mathcal{N}(x)$ である。

逆に， $N\in \mathcal{N}(x)$ とする。

N_0=\{y\in X\mid N\in \mathcal{N}(y)\}

とすると， $x\in N_0$ であり，さらに2.より， $N_0\subset N$ もわかる。また， $a\in N_0$ とすると， $N_0$ の定義より $\ N \in \mathcal{N}(a)$ である。5.から，ある $M\in\mathcal{N}(a)$ が存在して， $b\in M \implies N\in \mathcal{N}(b)$ となる。 $N_0$ の定義より， $M\subset N_0$ である。3.より， $N_0\in \mathcal{N}(a)$ である。以上と $\mathcal{O}$ の定義より， $N_0\in \mathcal{O}$ である。 $x\in N_0\subset N$ かつ $N_0\in \mathcal{O}$ なので， $N\in\mathcal{V}(x)$ であり， $\mathcal{N}(x)\subset \mathcal{V}(x)$ も示された。

証明終

5.は最後の近傍系の一致のところのみで使いました。

基本近傍系の定義と具体例

$x$ の近傍系 $\mathcal{N}(x)$ とは， $x$ の近傍を全部集めたものでしたが，基本近傍系はそうではありません。

定義3（基本近傍系）

$(X, \mathcal{O})$ を位相空間とし， $x\in X$ に対し， $\mathcal{N}(x)$ を $x$ の近傍系とする。

$\mathcal{B}(x)\subset \mathcal{N}(x)$ が $x$ の基本近傍系 (neighbourhood basis) であるとは，任意の $N\in \mathcal{N}(x)$ に対し，ある $B\in \mathcal{B}(x)$ が存在して，

\Large\color{red} x\in B\subset N

とできることをいう。

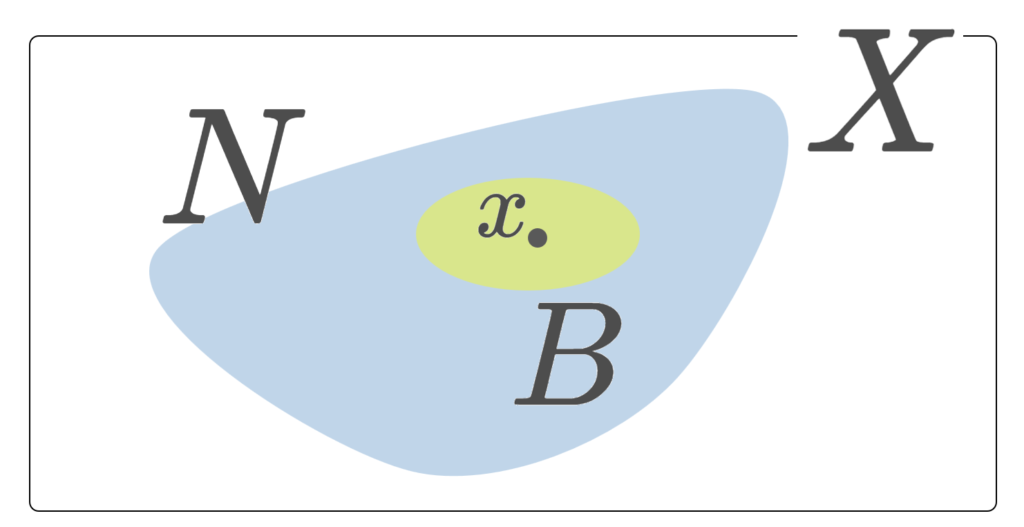
基本近傍系とは，どんなに小さな近傍を取ってきても，その近傍に含まれる集合が基本近傍系の中から取ってこれるような集合族です。まるで，最初の「距離空間における近傍」を定義したときのようですね。 $\{B_\varepsilon (x)\}_{\varepsilon >0}$ も基本近傍系の一種です。

定義より明らかに $\mathcal{N}(x)$ そのものは基本近傍系ですし，また，開近傍全体の集合も，基本近傍系です。近傍系は近傍「全て」を集めるので，各点 $x$ ごとに一通りに決まりますが，基本近傍系はさまざまな取り方があるため，一通りに決まりません。

基本近傍系の例1.

$(X,d)$ を距離空間とし， $x\in X$ とする。このとき，

$\{ B_\varepsilon (x)\}_{\varepsilon >0}$ は $x$ の基本近傍系である
$\{ B_{1/n}(x)\}_{n\ge 1}$ は $x$ の基本近傍系である
$\{ B_n(x)\}_{n\ge 1}$ は，一般には $x$ の基本近傍系とはいえない

2.が重要な例で， $n$ を十分大きくすると任意に小さいものが取れるので，基本近傍系の定義みたしています。このように，どんな「小さな」近傍を取ってこれても，さらに「小さな」ものが基本近傍系から持ってこれるかが重要です。一方，3.では，たとえば $B_{1/2}(x)$ に含まれるような基本近傍系の元がないのでダメです。

近傍は大きいものではなく，小さいものに興味があります。基本近傍系も「小さな」ものがきちんと網羅されているかが重要です。

基本近傍系の例2(密着空間).

$(X, \{\emptyset, X\})$ を空でない密着空間とする。このとき， $x\in X$ の基本近傍系は $\{X\}$ に限る。

基本近傍系の例3(離散空間).

$(X, 2^X)$ を空でない離散空間とする。このとき， $x\in X$ に対し， $\{x\}$ は $x$ の基本近傍系である。

離散空間においては， $\{x\}$ は $x$ の近傍の一つであり， $x$ のどんな近傍も， $\{x\}$ を部分集合として持ちます。

基本近傍系の性質

近傍系の性質と類似のことが，基本近傍系の性質にもあります。

定理3（近傍・近傍系の性質）

位相空間 $(X,\mathcal{O})$ の各点 $x\in X$ における基本近傍系 $\mathcal{B}(x)$ が定められているとする。このとき，以下が成り立つ。

すべての $x\in X$ について， $\mathcal{B}(x)\ne \emptyset$
$B\in\mathcal{B}(x)$ ならば $x\in B$
$B_1, B_2\in \mathcal{B}(x)$ ならば，ある $B\in \mathcal{B}(x)$ が存在して $B\subset B_1\cap B_2$ とできる
任意の $B\in \mathcal{B}(x)$ について，ある $A\in\mathcal{B}(x)$ が存在して，
$y\in A\implies \exists C\in \mathcal{B}(y) , \, C\subset B$
とできる。

1.と2.は明らかだと思うので，3.と4.を証明しましょう。

3, 4.の証明

3.について， $B_1\cap B_2$ は $x$ の近傍であるから，基本近傍系の定義より，ある $B\in\mathcal{B}(x)$ があって， $B\subset B_1\cap B_2$ とできる。

4.について， $\operatorname{Int}(B)$ は $x$ の近傍なので， $B' \subset \operatorname{Int}(B)$ となる $B'\in\mathcal{B}(x)$ が存在する。 $A=B'$ とすればよい。実際， $y\in A(\subset \operatorname{Int}(B)\subset B)$ に対し， $B$ は $y$ の近傍になるからである。

証明終

基本近傍系から位相を定める

定理4（近傍系から位相を定める）

$X$ を空でない集合とし，各 $x\in X$ に対し，集合族 $\mathcal{B}(x)\subset 2^X$ が定まっているとする。 $\mathcal{B}(x)$ が以下の条件をみたすとする(定理3の1.～4.と同じ)。

すべての $x\in X$ について， $\mathcal{B}(x)\ne \emptyset$
$B\in\mathcal{B}(x)$ ならば $x\in B$
$B_1, B_2\in \mathcal{B}(x)$ ならば，ある $B\in \mathcal{B}(x)$ が存在して $B\subset B_1\cap B_2$ とできる
任意の $B\in \mathcal{B}(x)$ について，ある $A\in\mathcal{B}(x)$ が存在して，
$y\in A\implies \exists C\in \mathcal{B}(y) , \, C\subset B$
とできる。