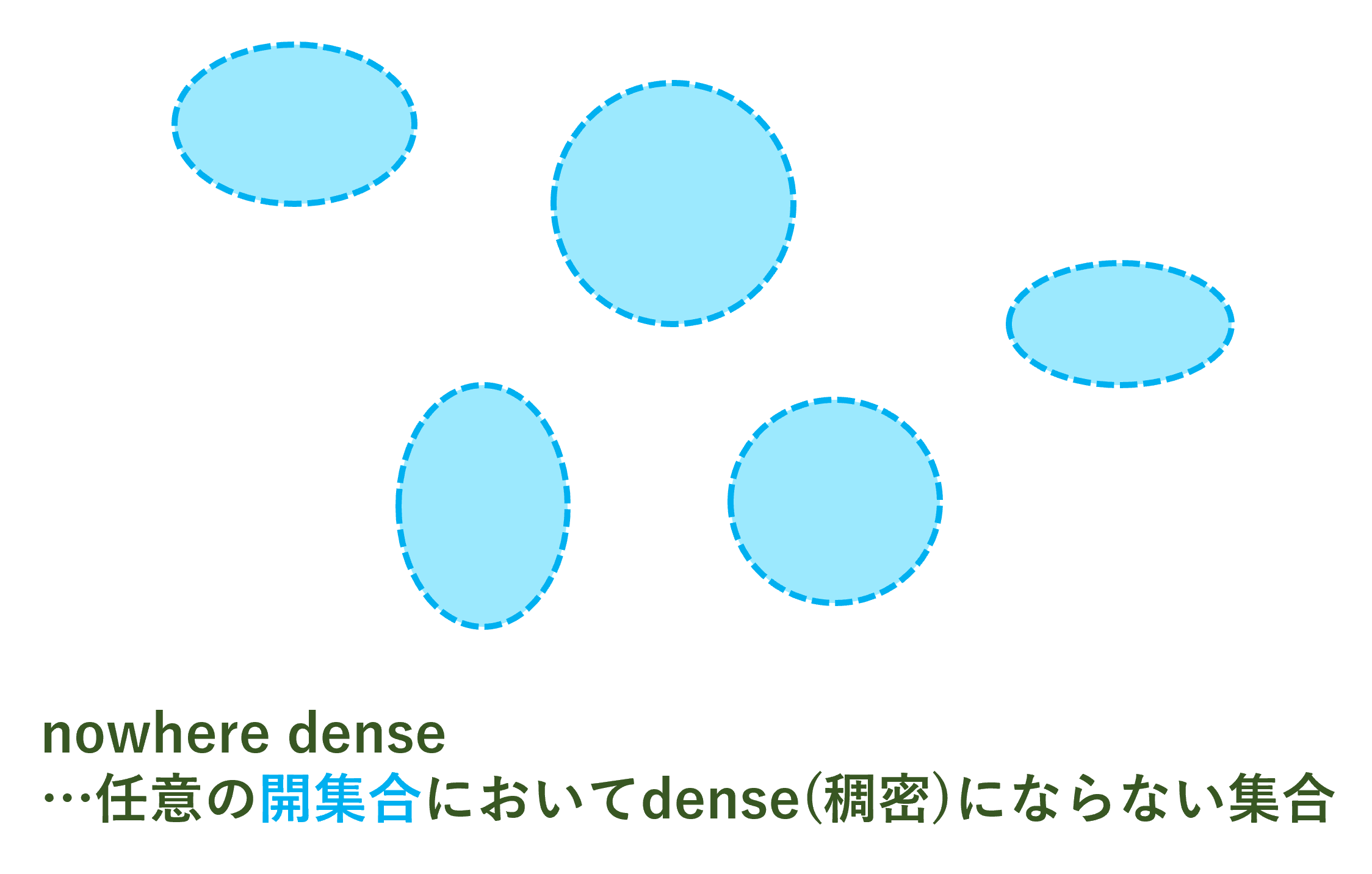
位相空間において nowhere dense set (疎集合) であるとは,閉包の内部(開核)が空であるような集合のことをいいます。どんな開部分集合上の相対位相で考えても,稠密にならない集合のことをいいます。
nowhere dense(疎集合) について,定義・例・性質を解説しましょう。
nowhere dense(疎集合)
復習ですが, Y\subset X が稠密 (dense) であるとは,\overline{Y}=X となること,すなわち閉包が全体集合になることをいいます(→【位相空間】稠密性と可分性~定義と具体例11個~)。
定義(nowhere dense; 疎集合)
(X,\mathcal{O}) を位相空間とする。 A\subset X が nowhere dense (疎集合) であるとは,
\Large\color{red} \operatorname{Int}(\overline{A})=\emptysetnowhere dense の言葉の意味を考えると,「どこをみても dense (稠密)でない」ということです。 x\in \operatorname{Int}(\overline{A}) とすると, x のある開近傍 U で, x\in U\subset \overline{A} となります。このとき,U\cap\overline{A}=U ですから, U\cap A は U の相対位相で稠密ということになります。
すなわち, A\subset X が nowhere dense であるとは,どの点の近傍 U を取っても, U\cap A がその近傍内で稠密にならないということになります。
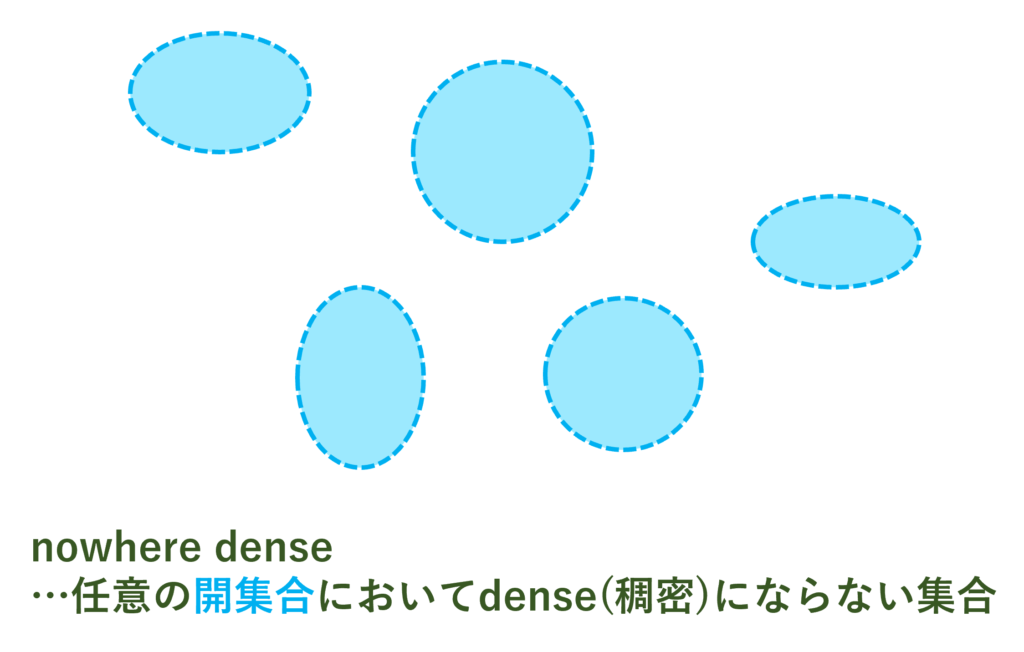
また, \operatorname{Int}(\overline{A})=\emptyset\iff \overline{X\setminus \overline{A}}=X ですから, A が nowhere dense \iff X\setminus \overline{A} が dense (稠密) です。
明らかに nowhere dense ならば dense (稠密)ではありません。対偶で,dense (稠密) ならば nowhere dense ではありません。
nowhere dense とそうでない集合の具体例
例1( \R).
\R において,
- \mathbb{Q} は dense であり,nowhere dense でない
- \mathbb{Q}\cap (0,1) は dense でない,nowhere dense でもない
- \mathbb{Z} は nowhere dense である
- カントール集合(カントールの三進集合)は nowhere dense である
- A\subset \R が nowhere dense であるとすると, \R\setminus A は dense である
2.は \operatorname{Int}(\overline{\mathbb{Q}\cap (0,1)}) = (0,1) なので,nowhere dense ではないです。 (0,1) という部分空間では, \mathbb{Q}\cap (0,1) は dense ですからね。
4.については,カントール集合はそもそも閉集合で,その内部(開核)は空です。非可算な nowhere dense の例です。
例2(太ったカントール集合).
[0,1] 区間の真ん中の幅 1/4 の開区間 (3/8, 5/8) を取り除き,残った2つの閉区間からそれぞれ真ん中の幅 1/4^2 の開区間を取り除き,残った4つの閉区間から,それぞれ真ん中の幅 1/4^3 の開区間を取り除き,……
という操作を無限回行って残った集合は,正の測度をもつ nowhere dense 集合である。
n 回目のステップで,各区間の真ん中の幅 1/3^n を取り除くのを繰り返すのが通常のカントール集合なのに対し,今回は, n 回目のステップで,各区間の真ん中の幅 1/4^n を取り除くのを繰り返すのが今回の集合です(これを太ったカントール集合ということがあります)。この集合は,カントール集合と同相であり,nowhere dense ですが,測度は
1-\left( \frac{1}{4} + \frac{2}{16} + \frac{4}{32}+\cdots\right) = \frac{1}{2}
となります。よって,この例は正測度をもつ nowhere dense 集合となります。
まあそもそも,今回の集合と測度 0 のカントール集合が同相になる時点で,位相が同相であることは測度を保たないので,そんな変な例ではないのかもしれませんね。他にも, (0,1)\cong \R ですが,両者の測度は異なります。
\overline{A}=X です。
\operatorname{Int}(\overline{A})=A です。
例5.
\ell^2 空間
\ell^2=\left \{ (x_n)\subset \R\middle| \sum_{n=1}^\infty x_n^2<\infty\right\}
はユークリッド距離によってヒルベルト空間と思える。 S \colon \ell^2 \to \ell^2 をシフト作用素
とすると, S は等長だが, S(\ell^2)\subset \ell^2 は nowhere dense である。
任意の \varepsilon-近傍は \ell^2\setminus S(\ell^2) と共通部分をもつので, \ell^2\setminus S(\ell^2) は dense (稠密) すなわち S(\ell^2) は nowhere dense です。
例6(右順序位相).
\R の部分集合族について,
\mathcal{O}_r =\{\emptyset, \R\}\cup \{ (a,\infty)\mid a\in\R \}
と定めると, (\R, \mathcal{O}_r) は位相空間になる。この位相を右順序位相 (right order topology) またはスコット位相 (Scott topology) という。
このとき, a\in \R について, (-\infty, a) は nowhere dense である。
\operatorname{Int}(\overline{(-\infty, a)}) = \operatorname{Int}((-\infty, a])= \emptyset なので, (-\infty, a) は nowhere dense です。右順序位相の位相的性質は以下で解説しています。
nowhere dense の性質
定理 (nowhere dense の性質)
(X,\mathcal{O}) を位相空間とする。このとき,
1.はほぼ明らかでしょう。2.と3.を示します。
2.と3.の証明
2.の \implies について
O\subset X を開集合とし, \partial O をその境界とする。 \partial O= \overline{O}\setminus O であるから, \partial O は閉集合である。
また, x\in \partial O と x の任意の開近傍 U に対し, U\cap O\ne \emptyset 特に U\not\subset \partial O であるから, \partial O は nowhere dense である。
2.の \impliedby について
F\subset X を nowhere dense な閉集合とする。このとき, O=X\setminus F とおくと, O は開集合である。
また, F は nowhere dense より,x\in F と x の任意の開近傍 U に対し, U\cap O\ne \emptyset である。これは,\overline{O}=X を意味するので, F = \partial O である。
3.について
A,B\subset X が nowhere dense なら, A\cup B が nowhere dense であることを示せば後は帰納法で分かるので良い。さらに1.より, A, B は閉集合としてよい。
A, B は nowhere dense であることは, X\setminus A,\, X\setminus B は dense (稠密) であることと同値である。後者より,任意の開集合 U に対し,U\cap (X\setminus A)\ne\emptyset であり,さらにこれも開集合なので, U\cap (X\setminus A) \cap (X\setminus B)\ne\emptyset である。これは, (X\setminus A) \cap (X\setminus B)= X\setminus (A\cup B) が dense (稠密) であることを意味するが,それはすなわち A\cup B が nowhere dense であることと同値である。
証明終
3.については,可算個の和集合では成り立ちません。 \mathbb{Q} は1点集合の可算和ですが,nowhere dense ではありません。
関連する概念
いくつか関連する概念を列挙しておきましょう
| 稠密 (dense) | 閉包が全体集合 |
| nowhere dense (疎集合) | 閉包の内部(開核)が空である |
| dense-in-itself (自己稠密) | 孤立点をもたない |
| 第一類集合 (1st category) | nowhere dense 集合の可算和 |
| 第二類集合 (2nd category) | 第一類集合でない集合 |
| ベール空間 (Baire space) | 稠密な開集合の可算個の共通部分が常に稠密になるような位相空間 |