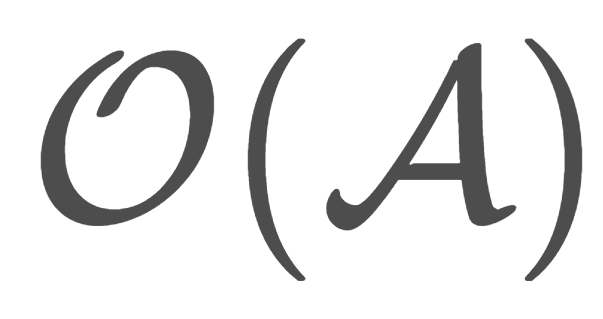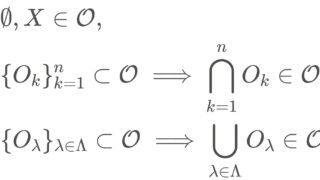開基・準開基とは,位相空間における「基底」のような概念で,それをみれば,位相空間全体が分かるようなものです。開基・準開基の厳密な定義と具体例を紹介し,さらに,位相空間全体を生成することを,開基・準開基を絡めて考えてみましょう。
開基の定義と具体例と性質
開基とは開集合族の部分集合で,「これを貼り合わせれば,開集合が全部作れるよ」というものです。
開基の定義
定義1(開基)
(X,\mathcal{O}) を位相空間とする。\mathcal{B}\subset \mathcal{O} が開基 (基底, basis, open base) であるとは,
任意の開集合 O\in \mathcal{O} に対し,ある \mathcal{B}_0\subset \mathcal{B} が存在して,
\Large \color{red} O= \bigcup_{B_0\in\mathcal{B}_0} B_0
とできることをいう。
すなわち,全ての開集合 O が,開基に属するいくつか(無限でも良い)の集合の和集合でかけると言っているんですね。開基の取り方はいろいろあり,たとえば \mathcal{O} そのものも開基です。
開基の定義は,次と同値です。
定理1(開基の同値な定義)
(X,\mathcal{O}) を位相空間とし,\mathcal{B}\subset \mathcal{O} とする。このとき,次は同値である。
- \mathcal{B} は開基である
- 任意の開集合 O\in\mathcal{O} と任意の x\in O について,ある B_{x}\in \mathcal{B} が存在して,
\Large x\in B_{x}\subset O
とできる。
よって,開基を2.のように定義しても構いません。2.の方が使いやすいことも多いです。
証明
1.\implies 2.について
O\in\mathcal{O} とすると,ある \mathcal{B}_0\subset \mathcal{B} が存在して, O= \bigcup_{B_0\in\mathcal{B}_0} B_0 とできる。したがって,任意の x\in O をとると, x\in B_0\subset O となる B_0\in \mathcal{B}_0 が取れる。
2. \implies 1.について
O\in\mathcal{O} に対して, \bigcup_{x\in O} B_{x} = O なので, \mathcal{B}_0=\{ B_{x}\mid x\in O\} とすればよい。
証明終
開基の具体例
開基の例1(\R).
\R に通常の位相を入れたものを考える。このとき,
- \{ (a,b)\mid a,b\in \R\} は開基である
- \{ (a,b )\mid a,b\in \mathbb{Q}\} も開基である
- \{ (q-1/n, q+1/n)\mid q\in \mathbb{Q}, n\ge 1\} も開基である
1.が開基であることは,定理1.2の方の定義を使うのが分かりやすいでしょう。任意の開集合 O\subset \R と, x\in O に対して,ある \varepsilon >0 が存在して, (x-\varepsilon, x+\varepsilon)\subset O とできますね。
2.や3.についても同様です。たとえば3.について,任意の開集合 O\subset \R と, x\in O に対して,1.のように (x-\varepsilon, x+\varepsilon)\subset O となる \varepsilon>0 をとります。 1/n <\varepsilon /2 となる n\ge 1 と,, |q-x|<1/n となる q\in \mathbb{Q} を取ってくることによって,
x\in (q-1/n, q+1/n)\subset (x-\varepsilon, x+\varepsilon)\subset O
とできますね。よって定理1.2の方の定義より,開基であることが分かります。
開基の例2(距離空間).
(X, d) を距離空間とし, B_\varepsilon (x)=\{ y\in X\mid d(x,y)<\varepsilon\} を x\in X の \varepsilon-近傍とする。このとき,
- \{ B_{\varepsilon}(x)\mid x\in X, \, \varepsilon>0 \} は開基である
- \{ B_{1/n}(x)\mid x\in X, \, n\ge 1\} も開基である
証明は,やはり定理1.2の方の定義を用いるとよいでしょう。
開基の例3(密着空間).
(X, \{ \emptyset, X\}) を密着空間とする。この空間の開基は \{X\} と \{\emptyset, X\} の2通りの取り方しかない。
開基は開集合族 \{ \emptyset, X\} の部分集合でなければならないことに注意してください。
開基の例4(離散空間).
(X, 2^X) を離散空間とする。このとき, \{ \{ x\} \mid x\in X\} は開基である。
開基の性質
定理2(開基の性質)
(X,\mathcal{O}) を位相空間とし,\mathcal{B}\subset \mathcal{O} を開基とする。このとき,以下が成立する。
- X = \bigcup_{B\in\mathcal{B}} B
- B_1, B_2\in\mathcal{B} とする。このとき,ある \mathcal{B}_0\subset \mathcal{B} が存在して,
\bigcup_{B_0\in\mathcal{B}_0} B_0 =B_1\cap B_2
とできる。
当たり前と思ったかもしれませんが,逆に,この性質1, 2.が成り立つとき,集合族 \mathcal{B} は,必ずある位相の開基となります。これは,あとの「位相の生成」で扱います。
証明
1.は開基の定義と, X 自体が開集合であることより明らか。
2.について, \mathcal{B}\subset \mathcal{O} であることより, B_1, B_2 は開集合であるから, B_1\cap B_2 も開集合である。よって開基の定義からわかる。
証明終
準開基の定義と具体例と性質
開基の概念は,開基の例1.や例2.のように,分かりやすい具体例も多く重要な概念ですが,さらに弱めた準開基という概念は,位相の生成を考えるうえで重要です。紹介しましょう。
準開基の定義
定義2(準開基)
(X,\mathcal{O}) を位相空間とする。\mathcal{S}\subset \mathcal{O} が準開基 (準基底, subbasis, subbase) であるとは, \mathcal{S} 内の有限個の共通部分を集めた集合族
\mathcal{B}_\mathcal{S} = \left\{\bigcap_{k=1}^n S_k \middle| S_1, \ldots, S_n\in \mathcal{S}, \, n\ge 1 \right\}
が (X,\mathcal{O}) の開基となっていることをいう。
定義より明らかに開基ならば準開基です。「有限個の」共通部分であることが重要で,開集合の定義が,そもそも「有限個」でしか共通部分で閉じていなかったことに対応しています。
なお, \mathcal{B}_\mathcal{S} = \left\{\bigcap_{k=1}^n S_k \middle| S_1, \ldots, S_n\in \mathcal{S}, \, \textcolor{red}{\boldsymbol{n\ge 0}} \right\} として,n=0 のときは \bigcap_{k=1}^n S_k=X と考えることで, \mathcal{B}_\mathcal{S} に常に X を含むこともあります。この方が \mathcal{B}_\mathcal{S} が広がるため開基になりやすくなり,\mathcal{S} が準開基になりやすくなります。
開基と同様に,準開基の定義も以下と同値です。
定理3(準開基の同値な定義)
(X,\mathcal{O}) を位相空間とし,\mathcal{S}\subset \mathcal{O} とする。このとき,次は同値である。
- \mathcal{S} は準開基である
- 任意の開集合 O\in\mathcal{O} と任意の x\in O について,ある有限個の S_{1}, \ldots, S_{n}\in \mathcal{S} が存在して,
\Large x\in\bigcap_{k=1}^n S_{k}\subset O
とできる。
証明は定理1とほぼ同じなので省略します。
準開基の具体例
準開基の例(\R).
\R に通常の位相を入れたものを考える。このとき,
- \{(-\infty, b)\mid b\in \R\}\cup\{(a,\infty)\mid a\in \R\} は準開基であるが,開基ではない
- \{(-\infty, b)\mid b\in \mathbb{Q}\}\cup\{(a,\infty)\mid a\in \mathbb{Q}\} も準開基であるが,開基ではない
1.について,a<b に対して, (a,b)=(-\infty, b)\cap (a,\infty) とできることと, \{ (a,b )\mid a,b\in \mathbb{R}\} が開基であることから,準開基であることは分かります。一方で, (a,b) に含まれる元を取ってこれないので,定理1.2の開基の定義をみたしていないので,開基ではありません。
2.も, \{ (a,b )\mid a,b\in \mathbb{Q}\} も開基なことを考えると,1.のときと全く同じように分かります。
位相の生成
X を空でない集合とし, \mathcal{A}\subset 2^X を空でない部分集合族とします。このとき, \mathcal{A}\subset \mathcal{O} となる位相 \mathcal{O} が必ず存在します。実際,離散位相 2^X は \mathcal{A} を含む位相です。
\mathcal{A} を含む位相全体を
\mathscr{O}=\{ \mathcal{O}\supset \mathcal{A}\mid \mathcal{O}\text{ is a topology}\}
とします。このとき, \bigcap_{\mathcal{O}\in \mathscr{O}} \mathcal{O} も \mathcal{A} を含む位相になります。ゆえに,集合族 \mathcal{A} を含む最小の位相を考えることができます。これを。
と表し,\mathcal{A} によって生成される位相といいます。具体例を挙げましょう。
位相の生成の例.
X=\{a,b,c\} とし, \mathcal{A}=\{\{a,b\}\},\, \mathcal{B}=\{ \{a, b\}, \{a, c\}\} とすると,
\begin{aligned}\mathcal{O}(\mathcal{A})&=\{ \emptyset, \{a,b\}, X\}, \\ \mathcal{O}(\mathcal{B})&=\{ \emptyset, \{a\}, \{a,b\}, \{a,c\}, X\} \end{aligned}
である。
生成される位相と開基・準開基の関係
生成される位相と,開基・準開基の関係を述べましょう。
定理4(生成される位相)
X を空でない集合とし, \mathcal{A}\subset 2^X を部分集合族とする。\mathcal{A} によって生成される位相空間 (X, \mathcal{O}(\mathcal{A})) について,
- \mathcal{A} が以下をみたすとき, \mathcal{A} はこの位相の開基である。
- X = \bigcup_{A\in\mathcal{A}} A
- A_1, A_2\in\mathcal{A} とする。このとき,ある \mathcal{A}_0\subset \mathcal{A} が存在して,
\bigcup_{A_0\in\mathcal{A}_0} A_0 =A_1\cap A_2
とできる。
- \mathcal{A} が X= \bigcup_{A\in\mathcal{A}} A をみたすとき, \mathcal{A} はこの位相の準開基である。
また 2.より,\mathcal{A} に適宜 X を付け加えることで, \mathcal{A} を位相空間 (X, \mathcal{O}(\mathcal{A})) の準開基にできる。
1.の2つの条件は,定理2の条件と同じです。定理4を証明しましょう。 A と \mathcal{A} の区別に注意して読んでください。 A は X の部分集合,\mathcal{A} はべき集合 2^X の部分集合のときに使います。
証明
1.について
\begin{align}\mathcal{O}=\left\{ \bigcup_{A_0\in\mathcal{A}_0} A_0\middle| \mathcal{A}_0\subset \mathcal{A}\right\}\end{align}
とする(ただし, \mathcal{A}_0=\emptyset なら \bigcup_{A_0\in\mathcal{A}_0} A_0=\emptyset と考える)。
\mathcal{A} によって生成される位相(開集合族) \mathcal{O}(\mathcal{A}) は,開集合族による位相空間の定義から,和集合について閉じているため,\mathcal{O}\subset\mathcal{O}(\mathcal{A}) となる。\mathcal{O} 自体が開集合族による位相空間の定義をみたしていることを示せば,\mathcal{O}=\mathcal{O}(\mathcal{A}) となり,かつ \mathcal{O} の定義の形から \mathcal{A} が開基になることもわかるので,これを示そう。
- \emptyset\in\mathcal{O} であり,また1.の1つ目の仮定から X\in\mathcal{O} である。
- O_1, O_2\in\mathcal{O} とする。\mathcal{O} の定義より,\mathcal{A}_1, \mathcal{A}_2\subset \mathcal{A} が存在して,
O_1 = \bigcup_{A_1\in\mathcal{A}_1} A_1,\quad O_2 = \bigcup_{A_2\in\mathcal{A}_2} A_2 とできる。このとき,
\begin{aligned}O_1\cap O_2 &= \left(\bigcup_{A_1\in\mathcal{A}_1} A_1\right)\cap \left(\bigcup_{A_2\in\mathcal{A}_2} A_2\right) \\ &= \bigcup_{\substack{A_1\in\mathcal{A}_1 \\ A_2\in \mathcal{A}_2}} (A_1\cap A_2) \end{aligned}
1.の2つ目の仮定より,ある \mathcal{A}_0(A_1, A_2)\subset \mathcal{A} が存在して, \bigcup_{A_0\in \mathcal{A}_0(A_1, A_2)}A_0= A_1\cap A_2 とできる。ゆえに,
\begin{aligned}O_1\cap O_2 &= \bigcup_{\substack{A_1\in\mathcal{A}_1 \\ A_2\in \mathcal{A}_2}}\bigcup_{A_0\in \mathcal{A}_0(A_1, A_2)}A_0 \\ &= \bigcup_{A_0\in\mathcal{A}_0} A_0\end{aligned}
とできる。ただし,\mathcal{A}_0=\bigcup_{\substack{A_1\in\mathcal{A}_1 \\ A_2\in \mathcal{A}_2}}\mathcal{A}_0(A_1, A_2) とした。したがって, O_1\cap O_2\in \mathcal{O} である。 - \{O_\lambda\}_{\lambda\in\Lambda} \subset\mathcal{O} とする。各 O_\lambda\in\mathcal{O} について,\mathcal{O} の定義より, \mathcal{A}_\lambda\subset \mathcal{A} が存在して, O_\lambda = \bigcup_{A_0\in\mathcal{A}_\lambda} A_0 とかける。よって,
\begin{aligned} \bigcup_{\lambda\in\Lambda} O_\lambda &= \bigcup_{\lambda\in\Lambda}\bigcup_{A_0\in\mathcal{A}_\lambda} A_0 \\ &= \bigcup_{A_0\in\mathcal{A}_\Lambda} A_0 \end{aligned}
とできる。ただし,\mathcal{A}_\Lambda = \bigcup_{\lambda\in\Lambda} \mathcal{A}_\lambda とした。したがって, \bigcup_{\lambda\in\Lambda} O_\lambda\in \mathcal{O} である。
以上から,\mathcal{O} は開集合族になる。よって示せた。
2.について
\mathcal{B}_\mathcal{A} = \left\{\bigcap_{k=1}^n A_k \middle| A_1, \ldots, A_n\in \mathcal{A}, \, n\ge 1 \right\}
とおく。\mathcal{A} がある位相の準開基となるならば,\mathcal{B}_\mathcal{A} が開基であるはずである。\mathcal{B}_\mathcal{A} が1.の2つの仮定をみたすことを示す。
- 1つ目の仮定をみたすことは,2.の仮定から明らかである。
- A_1, A_2\in\mathcal{B}_\mathcal{A} とすると,ある A'_1, \ldots, A'_m\in \mathcal{A} と A''_1, \ldots, A''_n\in\mathcal{A} が存在して,
A_1 = \bigcap_{k=1}^m A'_k,\quad A_2= \bigcap_{k=1}^n A''_k
とかける。このとき,
\begin{aligned} &A_1\cap A_2 \\&= A'_1\cap \cdots \cap A'_m\cap A''_1\cap \cdots\cap A''_n\end{aligned}
とかけるので, A_1\cap A_2\in \mathcal{B}_\mathcal{A} である。ゆえに2つ目の仮定もみたす。
以上より,\mathcal{B}_\mathcal{A} は1.の2つの仮定をみたすので, \mathcal{O}(\mathcal{B}_\mathcal{A}) は \mathcal{B}_\mathcal{A} を開基とする位相,すなわち \mathcal{A} を準開基とする位相である。位相(開集合族)は有限個の共通部分に関して閉じているため, \mathcal{O}(\mathcal{A})=\mathcal{O}(\mathcal{B}_\mathcal{A}) である。
証明終
なお,\mathcal{A} が1.の2つの仮定を満たすとき,\mathcal{A} を開基とする位相は上の \mathcal{O} に限ります。なぜなら,\mathcal{A} を開基とする位相は,(1) 式の右辺のようにかけなければならないからです。2.の準開基も同様です。
開基と基本近傍系
最後に,開基と基本近傍系の関係について述べておきましょう。基本近傍系の定義ついては,近傍・近傍系と基本近傍系~定義・具体例から位相を定めるまで~を確認してください。
定理5(開基と基本近傍系)
(X,\mathcal{O}) を位相空間とし,\mathcal{B}\subset \mathcal{O} を開基とする。 x\in X に対し,
\mathcal{B}(x)=\{ B\subset X \mid x\in B\in \mathcal{B}\}
と定めると, \mathcal{B}(x) は x の基本近傍系である。
証明
まず, \mathcal{B}(x)\subset \mathcal{B}\subset \mathcal{O} より, \mathcal{B}(x) の元は開集合であり,またどの元も x を含むから, \mathcal{B}(x) の元は全て x の開近傍である。
N を x の近傍の一つとすると, x\in \operatorname{Int}(N) を意味する。ただし, \operatorname{Int}(N) は N の内部(開核, N に含まれる最大の開集合)である。 \operatorname{Int}(N) は開集合より,ある \mathcal{B}_0\subset \mathcal{B} が存在して,
\operatorname{Int}(N) = \bigcup_{B_0\in\mathcal{B}_0} B_0
とできる。ゆえに, x\in B_0 となる B_0\in\mathcal{B}_0\subset \mathcal{B} が存在する。 \mathcal{B}(x) の定義より,この B_0 は B_0\in \mathcal{B}(x) であり,
となる。取ってきた近傍 N より小さな近傍が \mathcal{B}(x) から取れたので, \mathcal{B}(x) は x の基本近傍系である。
証明終
高々可算個の開集合からなる開基をとれるような位相空間は,第二可算公理 (second axiom of countability) をみたすといい,各点で高々可算個の集合からなる基本近傍系をとれるような位相空間は第一可算公理 (first axiom of countability) をみたすといいます。上の定理より,第二可算ならば第一可算が成立します。
開基の例1.より, \R は第二可算です。
第一可算・第二可算については,それぞれ以下の記事で解説しています。