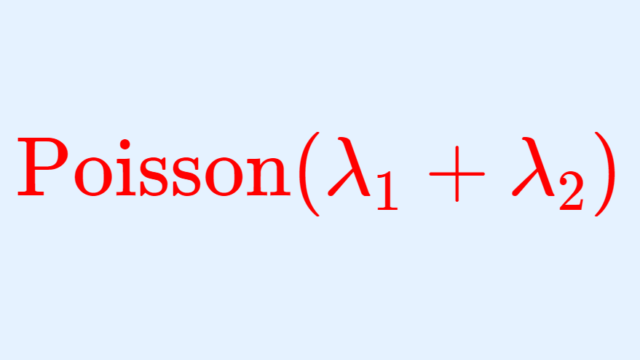 確率論
確率論 ポアソン分布の再生性とその2通りの証明
ポアソン分布には,「再生性 (reproductive property)」と呼ばれる性質があります。この性質について,その証明を,「定義から直接証明」「特性関数を用いた証明」の2通りで行いましょう。
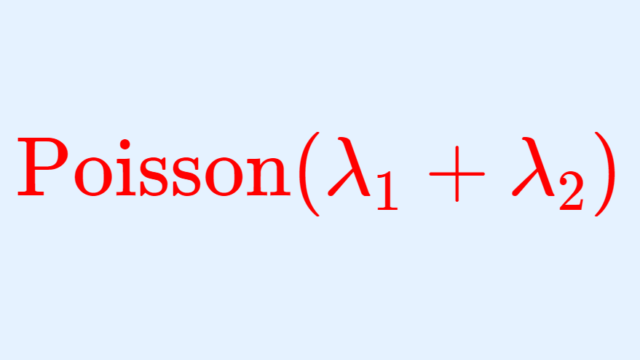 確率論
確率論 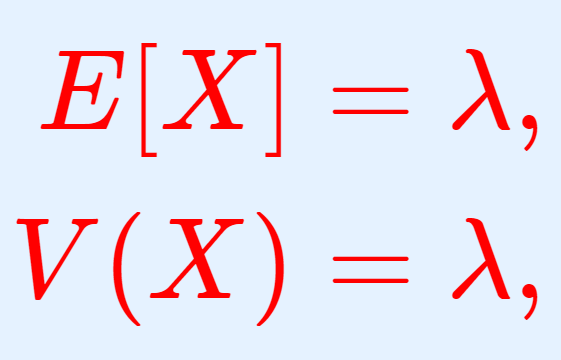 確率論
確率論 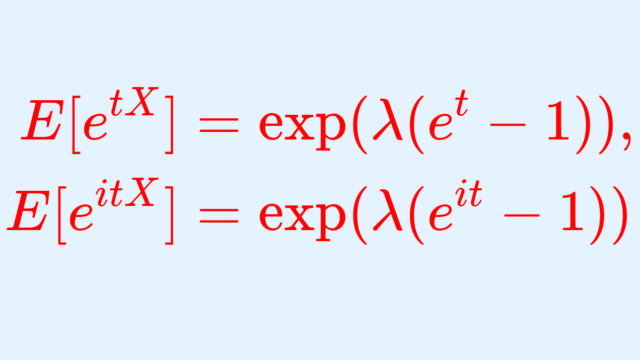 確率論
確率論 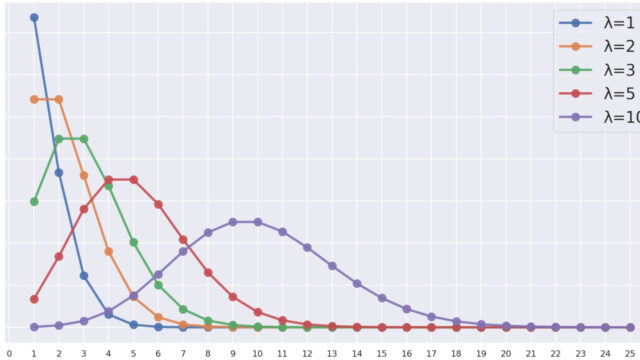 確率論
確率論  LaTeX
LaTeX  確率論
確率論  確率論
確率論  確率論
確率論  確率論
確率論  確率論
確率論