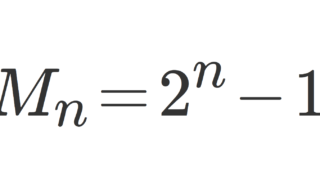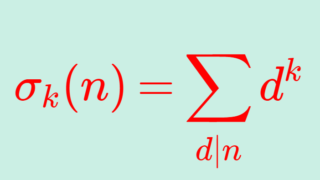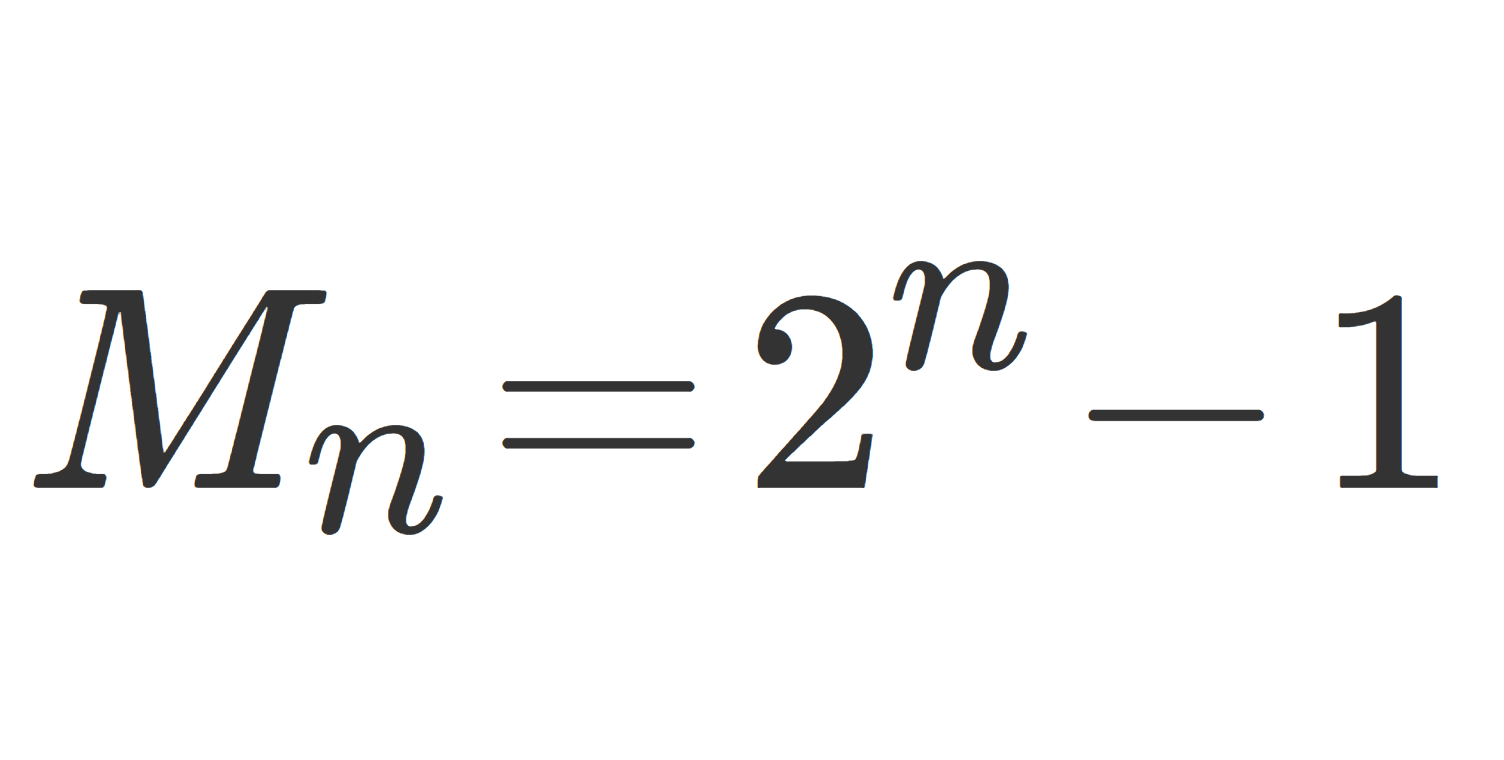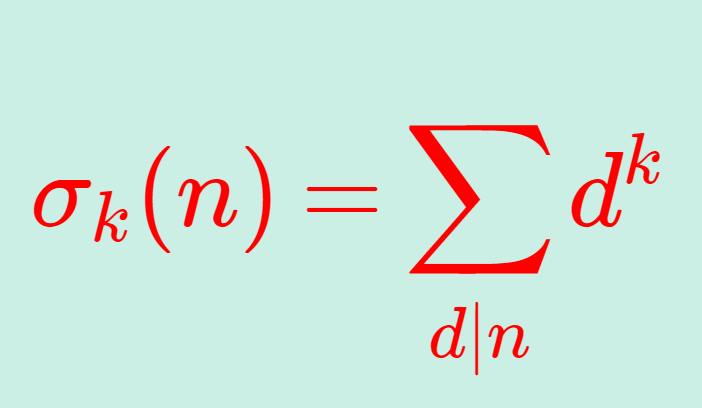完全数とは，自分以外の正の約数の総和が自分自身に一致する数のことです。たとえば， 28=1+2+4+7+14 は完全数です。
完全数について，その定義とメルセンヌ素数を絡めた性質を紹介しましょう。
完全数の定義
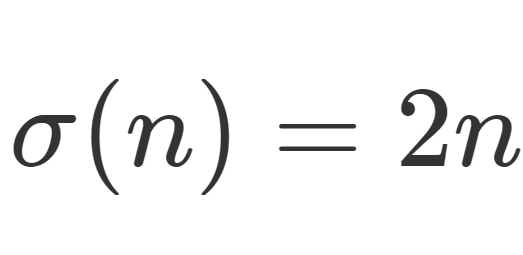
定義（完全数）
正の整数 n の正の約数の総和が 2n になるとき，n を完全数 (perfect number) という。
\color{red}\sigma(n) を n の正の約数の総和を表す関数(約数関数)とすると， \color{red}\sigma(n)=2n ということですね。言い換えると，自分以外の正の約数の総和が自分自身に一致する数ということができます。
たとえば， 6 = 1+2+3 や 28=1+2+4+7+14 は完全数の例です。他にも， 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128 は完全数です。
現在発見されている完全数は51個であり，「完全数は無数にあるか」「奇数の完全数は存在するか」は未解決問題です。
完全数の性質～完全数とメルセンヌ素数～
k を正の整数としたとき，\color{red}M_k = 2^k-1 と表せる数をメルセンヌ数 (Mersenne number) といい，これが素数のときメルセンヌ素数 (Mersenne prime) といいます(→メルセンヌ数・メルセンヌ素数とは～定義と性質～)。
偶数の完全数はメルセンヌ素数と関連があります。
定理（メルセンヌ素数と完全数）
- M_k = 2^k-1 が素数ならば 2^{k-1} M_k = 2^{k-1}(2^k-1) は完全数である。
- 偶数の完全数 n はあるメルセンヌ素数 M_k を用いて n=2^{k-1}M_k = 2^{k-1}(2^k-1) とかける。
偶数の完全数とメルセンヌ素数は対応しているといえますね。偶数の完全数は51個見つかっていますが，これはメルセンヌ素数が51個見つかっているからです。また前述したとおり，奇数の完全数の存在は未解決問題です。
なお， M_k =2^k-1 が素数 \implies k は素数であることが知られています(→メルセンヌ数・メルセンヌ素数とは～定義と性質～)。
証明
1. M_k=2^k-1 が素数なら 2^{k-1}M_k が完全数であること
M_k は奇数であるので， 2 とは異なる素数である。 2^{k-1}M_k の正の約数の総和 \sigma(2^{k-1}M_k) は
\begin{aligned} \sigma(2^{k-1}M_k) &=(1+2+\dots +2^{k-1}) (1+M_k) \\ &= \frac{2^k-1}{2-1} 2^k = 2^k M_k \end{aligned}
であるから，正の約数の総和は元の数の2倍である。よって完全数である。
2. 偶数の完全数は n=2^{k-1}M_k と表せること
n は偶数であるから，整数 k\ge 2 を用いて n = 2^{k-1} a ( a は奇数) と表せる。整数 m の正の約数の総和を \sigma(m) とする(約数関数)。一般に，互いに素な正の整数 m_1,m_2 に対し， \sigma(m_1m_2) = \sigma(m_1)\sigma(m_2) が成り立つ。したがって，
\begin{aligned} \sigma(n) &= \sigma(2^{k-1})\sigma(a) \\&= (1+2+\dots+ 2^{k-1}) \sigma(a) \\ &= (2^k-1) \sigma(a) \end{aligned}
となる。n は完全数なので， \sigma(n)=2n=2^k a である。ゆえに
であり， 2^k-1 ,2^k は互いに素であるから， (\sigma(a), a)=(2^k b, (2^k-1)b) \;\; (b\in\mathbb{Z}_{\ge 1}) と表せる。
であり， \sigma(2^k-1)\ge 2^k（等号成立は 2^k-1 が素数のとき）， \sigma(b)\ge b（等号成立は b=1 のとき）なので，
特に等号が成立するので， 2^k-1 が素数で， b=1 となる。故に a = 2^{k-1} (2^k-1) = 2^{k-1}M_k で M_k は素数である。
証明終
