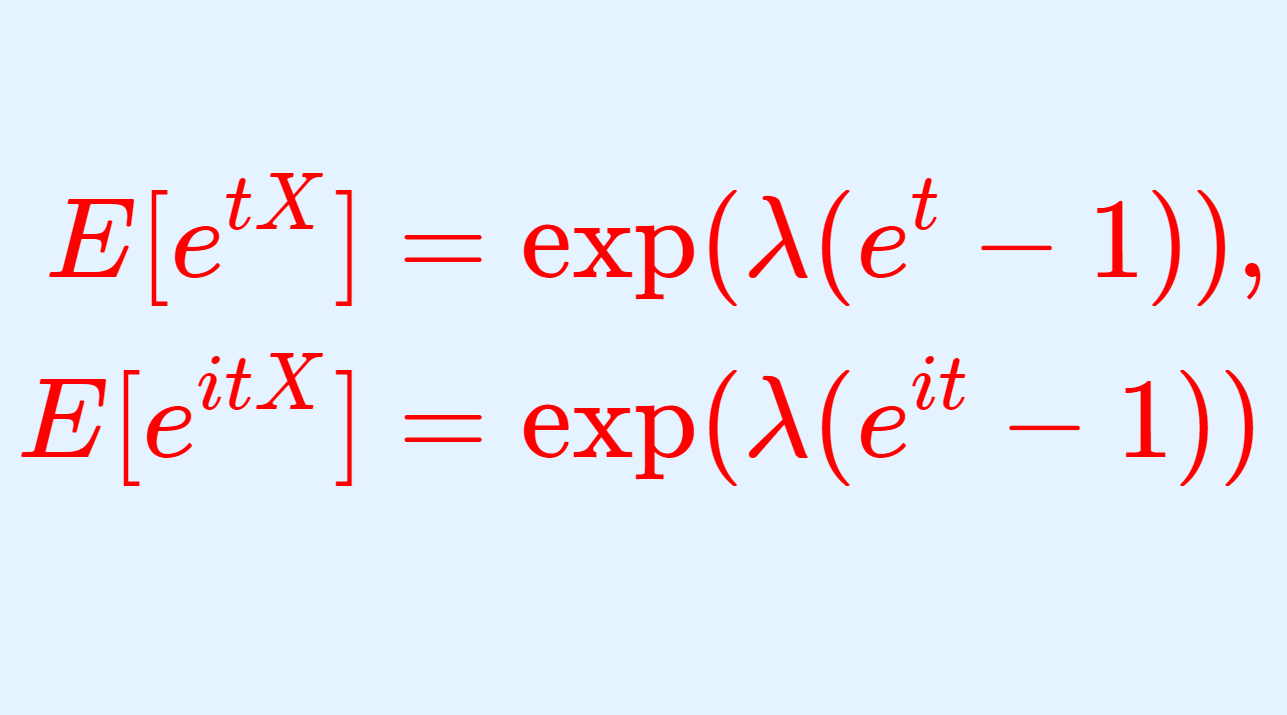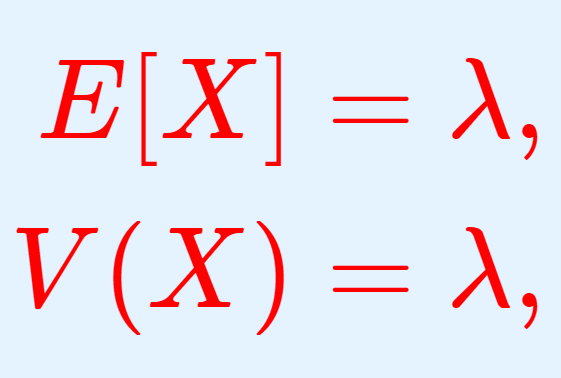ポアソン分布の積率母関数(モーメント母関数)・特性関数は,
\begin{aligned} E[e^{tX}] &= \exp (\lambda(e^t-1)), \\ E[e^{itX}]&= \exp(\lambda(e^{it}-1)) \end{aligned}
です。これについて,その導出の証明を行いましょう。
ポアソン分布の積率母関数(モーメント母関数)・特性関数
定理(ポアソン分布の積率母関数・特性関数)
X\sim \operatorname{Poisson}(\lambda) とする。このとき,X の積率母関数(モーメント母関数)・特性関数はそれぞれ
\color{red}\begin{aligned} E[e^{tX}] &= \exp (\lambda(e^t-1)), \\ E[e^{itX}]&= \exp(\lambda(e^{it}-1)) \end{aligned}
となる。
\exp x = e^x ですから,たとえば \exp (\lambda(e^t-1)) = e^{\lambda(e^t-1)} となります。累乗が二回出てきますから,こういうかき方はややこしいので, \exp を用いて記述しています。
証明に入る前に,ポアソン分布の定義を復習しておきましょう。
ポアソン分布の定義
X を確率変数, \lambda > 0 とする。 k=0,1,2,\ldots に対し,
\color{red} P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda }
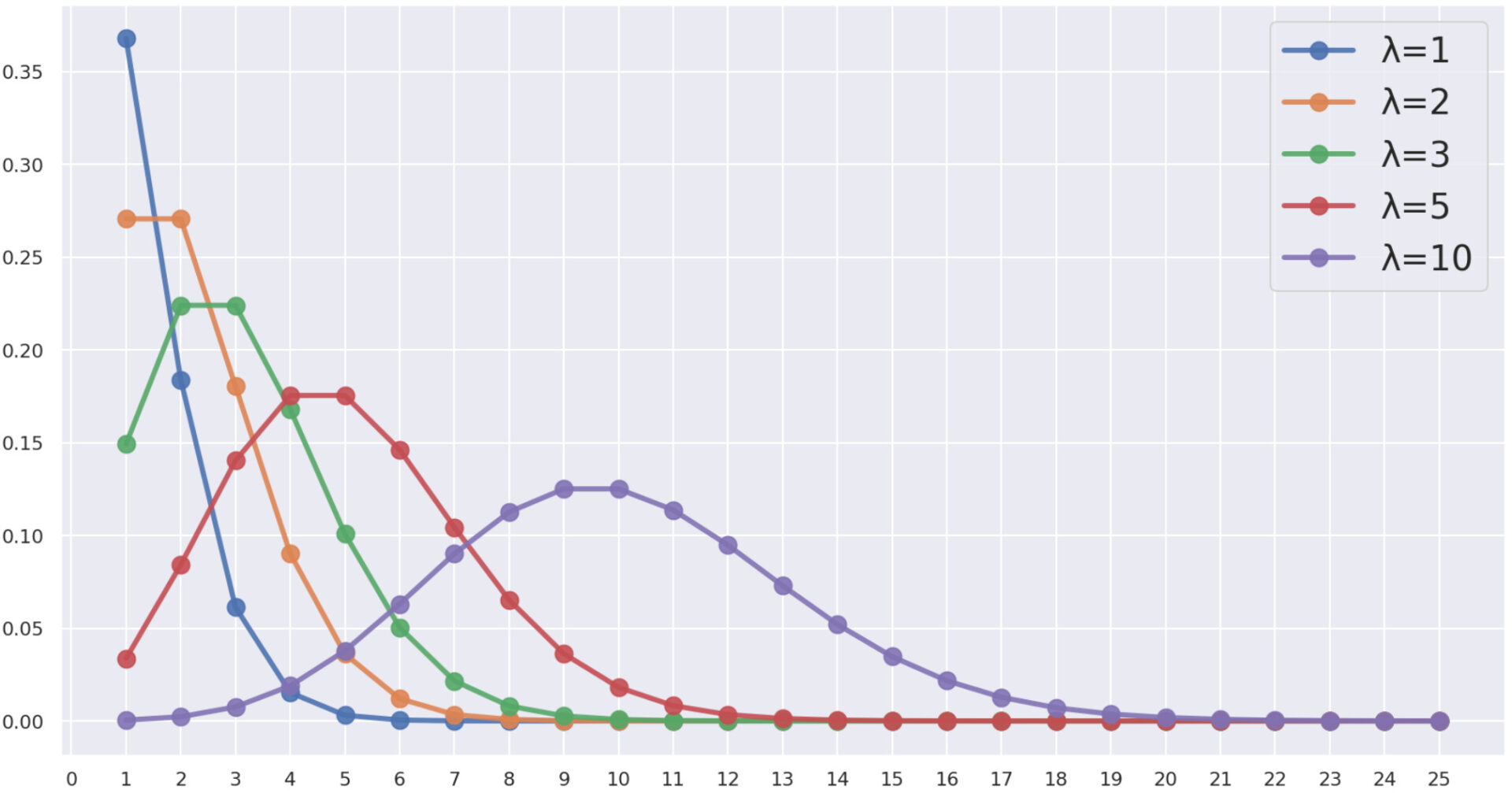
が成り立つとき, X はパラメータ \lambda のポアソン分布 (Poisson distribution) に従うという。本記事では,これを \color{red}X\sim \operatorname{Poisson}(\lambda) とかくことにする。
ポアソン分布は,「まれな事象が一定期間に起こる回数」をモデル化するのによく使います。詳しくは,以下の記事を参照してください。
ポアソン分布の積率母関数(モーメント母関数)・特性関数の導出証明
早速導出していきましょう。ここで必要な知識は, e^x のマクローリン展開です。
e^x = \sum_{n=0}^\infty \frac{x^n}{n!}
これを踏まえて,証明を確認していきましょう。
ポアソン分布の積率母関数(モーメント母関数)の導出
証明
期待値とポアソン分布の定義により,
\begin{aligned}E[e^{tX}] &= \sum_{k=0}^\infty e^{tk}P(X=k)\\ &= \sum_{k=0}^\infty e^{tk} \frac{\lambda^k}{k!}e^{-\lambda } \\ &= e^{-\lambda} \sum_{k=0}^\infty \frac{(\lambda e^t)^k}{k!} \\ &= e^{-\lambda} e^{\lambda e^t} \\ &= \exp (\lambda(e^t-1)) \end{aligned}
であるから,示せた。
証明終
ポアソン分布の特性関数の導出
特性関数の導出は,積率母関数(モーメント母関数)とほぼ同様ですが,やっていきましょう。
証明
期待値とポアソン分布の定義により,
\begin{aligned}E[e^{itX}] &= \sum_{k=0}^\infty e^{itk}P(X=k)\\ &= \sum_{k=0}^\infty e^{itk} \frac{\lambda^k}{k!}e^{-\lambda } \\ &= e^{-\lambda} \sum_{k=0}^\infty \frac{(\lambda e^{it})^k}{k!} \\ &= e^{-\lambda} e^{\lambda e^{it}} \\ &= \exp (\lambda(e^{it}-1)) \end{aligned}
であるから,示せた。
証明終
無事,導出できましたね。